
北师大版初中数学九年级上册期末测试卷(标准难度)(含答案解析)
展开北师大版初中数学九年级上册期末测试卷
考试范围:全册;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
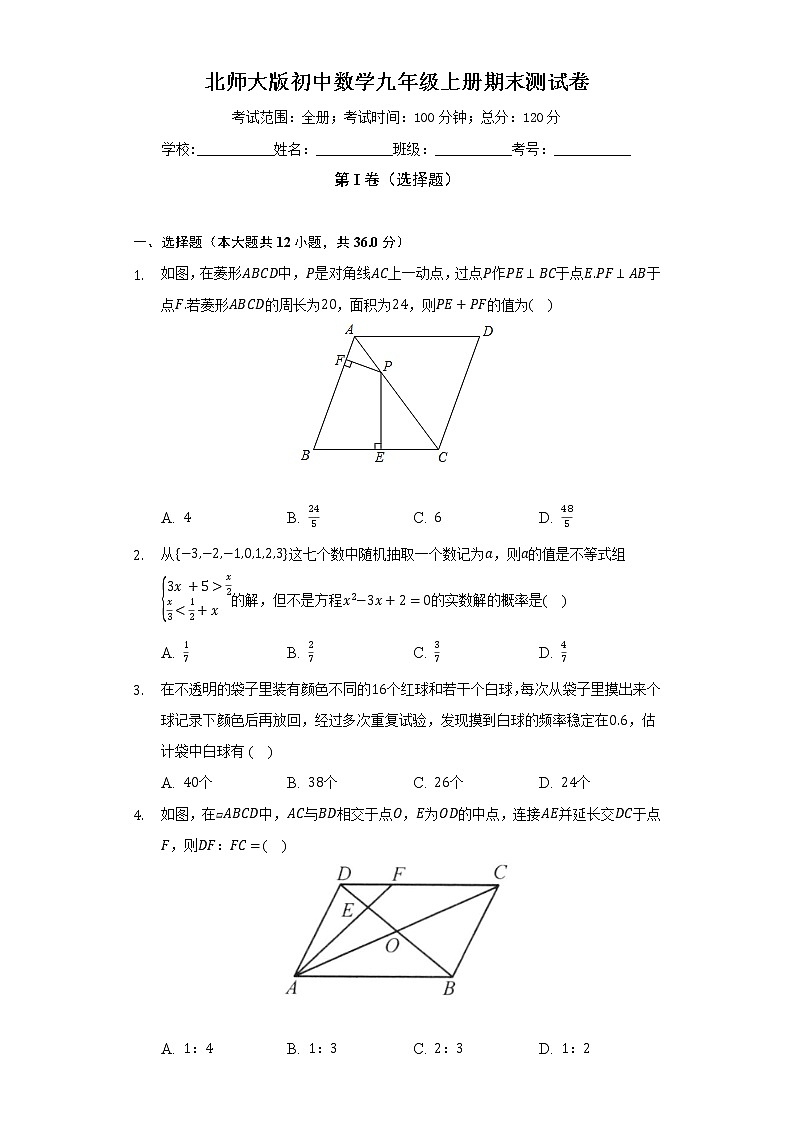
- 如图,在菱形中,是对角线上一动点,过点作于点于点若菱形的周长为,面积为,则的值为( )
A. B. C. D.
- 从这七个数中随机抽取一个数记为,则的值是不等式组的解,但不是方程的实数解的概率是( )
A. B. C. D.
- 在不透明的袋子里装有颜色不同的个红球和若干个白球,每次从袋子里摸出来个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在,估计袋中白球有( )
A. 个 B. 个 C. 个 D. 个
- 如图,在中,与相交于点,为的中点,连接并延长交于点,则:( )
A. : B. : C. : D. :
- 下列几何体的三种视图都是圆形的是( )
A. B. C. D.
- 如图,已知在平面直角坐标系中,直线分别交轴、轴于点和点,分别交反比例函数,的图象于点和点,过点作轴于点,连接,若的面积与的面积相等,则的值是( )
A. B. C. D.
- 如图,四边形是矩形,,,点在第二象限,则点的坐标是( )
A.
B.
C.
D.
- 如图,正方形的顶点分别在反比例函数和的图象上.若轴,点的横坐标为,则( )
A. B. C. D.
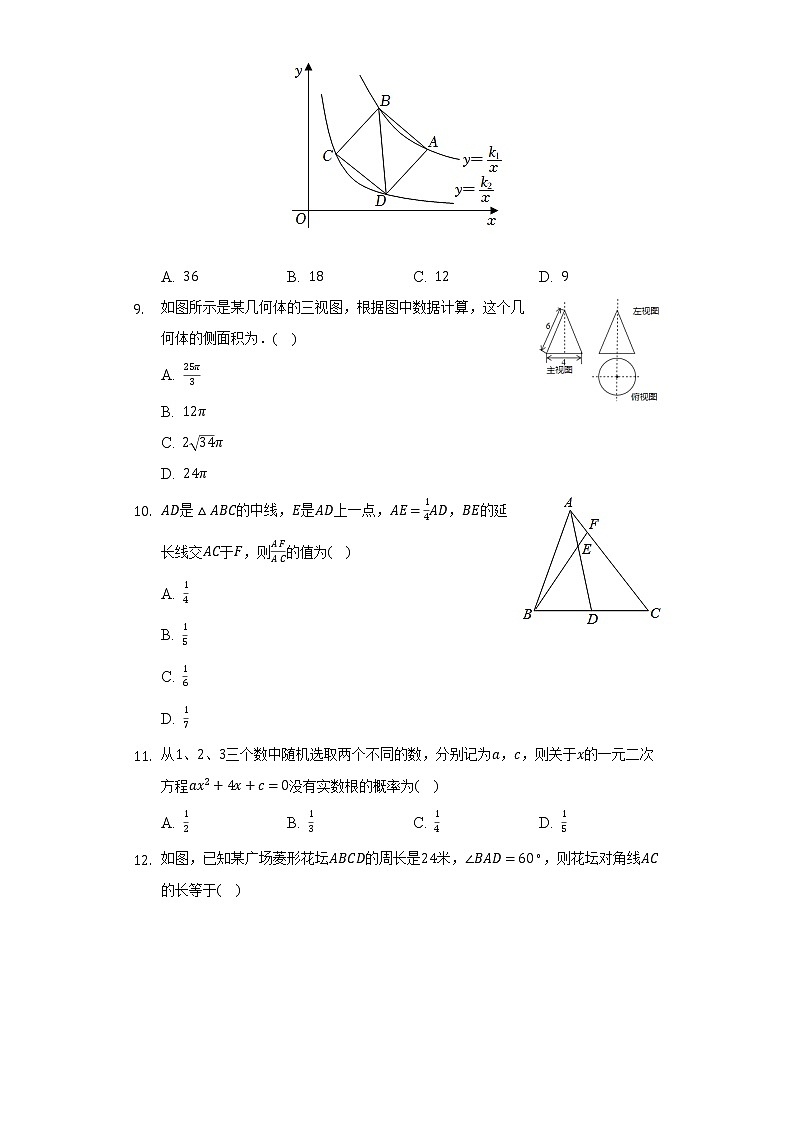
- 如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为.( )
A.
B.
C.
D.
- 是的中线,是上一点,,的延长线交于,则的值为( )
A.
B.
C.
D.
- 从、、三个数中随机选取两个不同的数,分别记为,,则关于的一元二次方程没有实数根的概率为( )
A. B. C. D.
- 如图,已知某广场菱形花坛的周长是米,,则花坛对角线的长等于( )
A. 米 B. 米 C. 米 D. 米
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
- 如图,菱形中,是的垂直平分线,,则______.
- 阅读理解:对于这类特殊的代数式可以按下面的方法分解因式:
.
理解运用:如果,那么,即有或,
因此,方程和的所有解就是方程的解.
解决问题:求方程的解为______. - 在不透明的甲、乙两个盒子中装有除颜色外完全相同的小球,甲盒中有个白球、个黄球,乙盒中有个白球、个黄球,分别从每个盒中随机摸出个球,则摸出的个球都是黄球的概率是______.
- 如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点在旋转中心的正下方.某一时刻,太阳光线恰好垂直照射叶片,,此时各叶片影子在点右侧成线段,测得,,垂直于地面的木棒与影子的比为:,则点,之间的距离等于______米.转动时,叶片外端离地面的最大高度等于______米.
三、解答题(本大题共8小题,共72.0分)
- 如图,正方形的对角线,相交于点,,为上一点,,连接,过点作于点,与交于点.
与相等吗?若相等,请证明;若不相等,请说明理由.
求的长.
- 已知关于的方程有实根.
当时,求解上述方程;
求的取值范围;
是否存在实数,使方程两根的倒数和为?若存在,请求出的值;若不存在,请说明理由. - 某品牌免洗洗手液按剂型分为凝胶型、液体型,泡沫型三种型号分别用,,依次表示这三种型号小辰和小安计划每人购买一瓶该品牌免洗洗手液,上述三种型号中的每一种免洗洗手液被选中的可能性均相同.
小辰随机选择一种型号是凝胶型免洗洗手液的概率是______.
请你用列表法或画树状图法,求小辰和小安选择同一种型号免洗洗手液的概率. - 如图,在中,,为中点,,且.
求证:四边形是矩形;
连接交于点,若,,求的长. - 如图,树在路灯的照射下形成投影若树高,树影,树与路灯的水平距离,求路灯的高度.
- 如图,在平面直角坐标系中,一次函数和的图象相交于点,反比例函数的图象经过点.
求反比例函数的表达式;
设一次函数的图象与反比例函数的图象的另一个交点为,连接,求的面积.
- 如图,已知四边形是矩形,点在的延长线上,与相交于点,与相交于点,.
求证:;
若,求的长;
如图,连接,求证:.
- 若关于,的二元一次方程组的解,.
求的取值范围;
若是一个直角三角形的直角边长,是其斜边长,此三角形另一条直角边的长为方程的解,求这个直角三角形的面积.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了菱形的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.
连接,如图,根据菱形的性质得,,然后利用三角形面积公式,由,得到,再整理即可得到的值.
【解答】
解:连接,如图,
四边形为菱形,菱形的周长为,
,,
,
,
.
2.【答案】
【解析】
【分析】
此题考查了概率公式的应用、不等式组的解集以及一元二次方程的解法.用到的知识点为:概率所求情况数与总情况数之比.
首先解不等式组,即可求得的取值范围,解一元二次方程,可求得可取的值,然后直接利用概率公式求解即可求得答案.
【解答】
解:,
由得:,
由得:,
,
的值是不等式组的解,
,,,,
,
,
解得:,,
不是方程的实数解,
或;
的值是不等式组的解,但不是方程的实数解的概率为:.
故选:.
3.【答案】
【解析】
【分析】
此题主要考查了利用频率估计概率,根据大量反复试验下频率稳定值即概率求解是解题的关键.由摸到白球的频率稳定在得出口袋中得到红色球的频率,进而求出球的总数即可求出白球的个数.
【解答】
解:由题意可得:红球的频率为,
球的总个数为:个,
则白球个数为:个.
故选D.
4.【答案】
【解析】
【分析】
本题考查了相似三角形的判定与性质以及平行四边形的性质,难度适中,解答本题的关键是根据平行证明∽,然后根据对应边成比例求值.首先证明∽,然后利用对应边成比例,为的中点,求出:的值,又知,即可得出:的值.
【解答】
解:在平行四边形中,,
则∽,
,
为对角线的交点,
,
又为的中点,
,
则::,
::,
,
::,
::.
故选D.
5.【答案】
【解析】解:选项的主视图和左视图为长方形,
选项不符合题意;
选项的三种视图都是圆形,
选项符合题意;
选项的主视图和左视图为等腰三角形,
选项不符合题意;
选项主视图和左视图为等腰梯形,
选项不符合题意;
综上,选项的三种视图都是圆形,
故选:.
利用三视图的知识,指出每个选项中几何体的三视图从而得出结论.
本题主要考查了简单几何体的三视图,准确指出每个几何体的三视图是解题的关键.
6.【答案】
【解析】
【分析】
本题考查一次函数与反比例函数的综合,属于中档题.
利用三角形面积相等进行转化求解是解题的关键.
【解答】
解:由题意可求,
直线与交于点,
,
设,
,
的面积与的面积相等,
,
,
,点在直线上,
,
,
故选:.
7.【答案】
【解析】
【分析】
本题考查了矩形的性质,全等三角形的判定和性质,坐标与图形的性质,正确的作出辅助线是解题的关键.
过作轴于,过作轴于,得到,根据矩形的性质得到,,根据全等三角形的性质得到,,,于是得到结论.
【解答】
解:过作轴于,过作轴于,
,
四边形是矩形,
,,
,
≌,
同理≌,
,,,
,,
,,,
,
点的坐标是,
故选:.
8.【答案】
【解析】解:连接交于,延长交轴于,连接、,如图:
四边形是正方形,
,
设,,
轴,
,,
,都在反比例函数的图象上,
,
,
,
,
在反比例函数的图象上,在的图象上,
,,
;
故选:.
连接交于,延长交轴于,连接、,设,,根据轴,可得,,即知,从而,,由在反比例函数的图象上,在的图象上,得,,即得.
本题考查反比例函数及应用,涉及正方形性质,解题的关键是用含字母的代数式表示相关点坐标.
9.【答案】
【解析】
【分析】
考查学生对三视图掌握程度和灵活运用能力,关键是由主视图和左视图确定是柱体,锥体还是球体.
由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状,确定圆锥的母线长和底面半径,从而确定其表面积.
【解答】
解:由主视图和左视图为三角形判断出是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;
根据三视图知:该圆锥的母线长为,底面圆直径为,则半径为,
故侧面积,
故选:.
10.【答案】
【解析】
【分析】
本题考查了平行线分线段成比例正确找到比例关系是解题的关键.
过点作交于,根据得到,,即可求出的值.
【解答】
解:过点作交于,
是的中线,
,
,
,,
,
,
的值.
故选D.
11.【答案】
【解析】解:画树状图如下:
共有种等可能的结果,其中满足,即的结果有、这种结果,
关于的一元二次方程没有实数根的概率为,
故选:.
画树状图,共有种等可能的结果,再找出满足的结果数,然后根据概率公式求解即可.
本题考查的是用树状图法求概率,树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.也考查了根的判别式.
12.【答案】
【解析】
【分析】此题考查了勾股定理,菱形的性质,以及等边三角形的判定与性质,熟练掌握菱形的性质是解本题的关键由四边形为菱形,得到四条边相等,对角线垂直且互相平分,根据得到三角形为等边三角形,在直角三角形中,利用勾股定理求出的长,即可确定出的长.
【解答】
解:设与的交点为,
四边形为菱形,
,,,米,
,
为等边三角形,
米,米,
在中,根据勾股定理得米,
则米.
故选A.
13.【答案】
【解析】
【分析】
本题考查了菱形的性质,线段垂直平分线的性质,熟练运用菱形的性质是本题的关键.
由菱形的性质可得,,可得,由线段垂直平分线的性质可得,即可求的值.
【解答】
解:四边形是菱形
,
是的垂直平分线
,
故答案为:
14.【答案】或或
【解析】解:,
,
,
,
则,即,
或,
解得或,
故答案为:或或.
将原方程左边变形为,再进一步因式分解得,据此得到两个关于的方程求解可得.
本题主要考查因式分解的应用,因式分解是研究代数式的基础,通过因式分解将多项式合理变形,是求代数式值的常用解题方法,具体做法是:根据题目的特点,先通过因式分解将式子变形,然后再进行整体代入.
15.【答案】
【解析】解:画树状图为:,
共有种等可能的结果数,其中个球都是黄球占种,
摸出的个球都是黄球的概率;
故答案为:.
先画出树状图展示所有种等可能的结果数,再找出个球都是黄球所占结果数,然后根据概率公式求解.
本题考查了列表法与树状图法:运用列表法或树状图法展示所有可能的结果求出,再从中选出符合事件或的结果数目,然后根据概率公式求出事件或的概率.
16.【答案】
【解析】解:如图,设与交于点,过点作于,
,
,
,
∽,
,即,
,
,
,
,
,
设,,则,
,
,
,
,
在中,,
,
,
,
,
以点为圆心,的长为半径作圆,当与共线时,叶片外端离地面的高度最大,其最大高度等于米.
故答案为:,
作辅助线,构建直角,证明∽,根据垂直于地面的木棒与影子的比为:,列比例式可得的长,由三角函数的定义可得的长,从而得,由此可解答.
本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
17.【答案】解:.
理由:,
.
四边形是正方形,
,,
,
.
在和中,
,
.
是等腰直角三角形,且,
.
,
,由勾股定理,得,
,
,
.
【解析】本题考查了正方形的性质、全等三角形的性质和判定,熟知正方形的四条边都相等,四个角都是直角,对角线互相垂直且相等平分,掌握相关的判定定理和性质定理是解题的关键.
利用正方形的性质得,,再利用等角的余角相等得到,则利用”“可判断≌,然后根据全等三角形的性质得到结论;
根据面积法列式可得的长.
18.【答案】解:,方程化为:,
,
或,
所以,;
当时,方程化为,方程有实数解;
当时,根据题意得,
解得且,
综上所述,的取值范围为;
不存在.
理由如下:
设方程的两根分别为、,
根据根与系数的关系得,,
,即,
,
,解得,
且,
不存在实数,使方程两根的倒数和为.
【解析】本题考查了根与系数的关系:若,是一元二次方程的两根时,,也考查了根的判别式.
利用因式分解法解方程即可;
讨论:当时,方程为一元一次方程,有实数解;当时,利用根的判别式的意义得到,此时满足且,然后综合两种情况得到的取值范围;
设方程的两根分别为、,根据根与系数的关系得,,再利用得到,解得,然后利用且可判断不存在实数,使方程两根的倒数和为.
19.【答案】解:;
列表如下:
| |||
由表可知,共有种等可能结果,其中小辰和小安选择同一种型号免洗洗手液有种结果,
所以小辰和小安选择同一种型号免洗洗手液的概率为.
【解析】小辰随机选择一种型号是凝胶型免洗洗手液的概率是,
故答案为:;
见答案
直接根据概率公式求解即可;
列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
20.【答案】证明:,,
四边形是平行四边形,
,为的中点,
,
,
四边形是矩形.
解:四边形是矩形,
,
,,
,
,
,
,
∽,
,
.
【解析】本题考查相似三角形的判定和性质,矩形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
先判断四边形是平行四边形,再根据有一个角是直角的平行四边形是矩形即可判断.
先由含角的直角三角形的性质求出,的长,进而得到的长,再由勾股定理求出的长,然后证明∽,推出,由此即可解决问题.
21.【答案】解:如图,可知,
则,
即,
解得.
答:路灯的高度是.
【解析】见答案
22.【答案】解:联立和并解得:,故点,
将点的坐标代入反比例函数表达式得:,解得:,
故反比例函数表达式为:;
一次函数与反比例函数表达式
联立并解得:或,
当时,,故点,
设交轴于点,过点、分别作轴的垂线交于点、,
则.
【解析】本题考查了反比例函数与一次函数的交点,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强.
联立和并解得:,故点,进而求解;
,即可求解.
23.【答案】证明:四边形是矩形,点在的延长线上,
,
又,,
,
,
,
即,
故BD,
解:四边形是矩形,
,
∽,
,
即,
设,则有,化简得,
解得或舍去,
.
如图,在线段上取点,使得,
在与中,,,,
,
,,
,
为等腰直角三角形,
.
【解析】本题是四边形综合题,考查了矩形的性质,相似三角形的判定与性质,全等三角形的判定与性质,等腰直角三角形的判定与性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
证明,得出,证得,则结论得出;
证明∽,得出,即,设,则有,化简得,解方程即可得出答案;
在线段上取点,使得,证明,得出,,证得为等腰直角三角形,可得出结论.
24.【答案】解:解方程组得
,,
解得,
的取值范围为.
,
解得,
、、分别是直角三角形的三边长,
,
解得,舍去,
,
三角形的面积为.
【解析】本题主要考查解二元一次方程组、一元一次不等式组、一元二次方程,勾股定理和三角形面积等知识的综合运用.
解关于,的二元一次方程组,根据,值大于可得关于的不等式组,解不等式组可求解;
先用配方法求得一元二次方程的解,再利用勾股定理计算可求解.
人教版初中数学九年级上册期末测试卷(标准难度)(含答案解析): 这是一份人教版初中数学九年级上册期末测试卷(标准难度)(含答案解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北师大版初中数学九年级上册期末测试卷(标准难度)(含答案解析): 这是一份北师大版初中数学九年级上册期末测试卷(标准难度)(含答案解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙教版初中数学九年级上册期末测试卷(标准难度)(含答案解析): 这是一份浙教版初中数学九年级上册期末测试卷(标准难度)(含答案解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。