北师大版初中数学九年级上册第五章《投影与视图》单元测试卷（困难）（含答案解析）

北师大版初中数学九年级上册第五章《投影与视图》单元测试卷

考试范围：第五章；考试时间：100分钟；总分：120分

学校:___________姓名：___________班级：___________考号：___________

第I卷（选择题）

一、选择题（本大题共12小题，共36.0分）

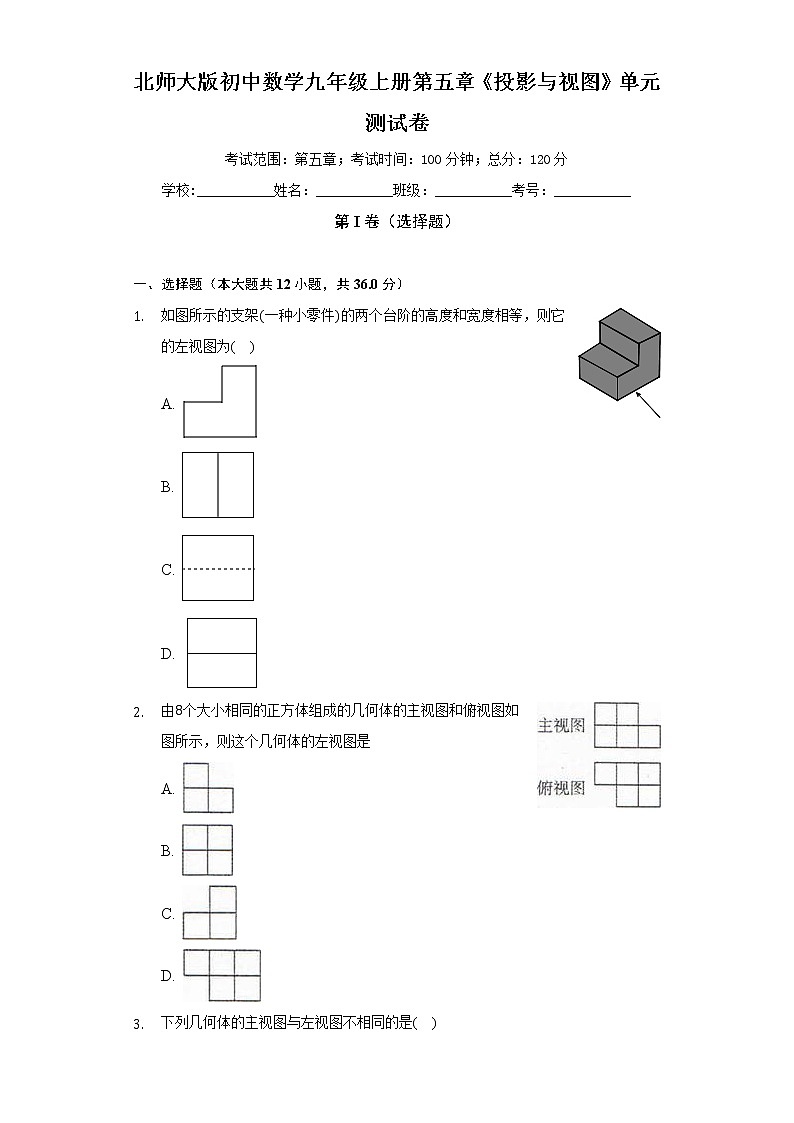
1. 如图所示的支架一种小零件的两个台阶的高度和宽度相等，则它的左视图为(    )

A.
B.
C.
D.

2. 由个大小相同的正方体组成的几何体的主视图和俯视图如图所示，则这个几何体的左视图是

A.
B.
C.
D.

3. 下列几何体的主视图与左视图不相同的是(    )

A.  B.
C.  D.

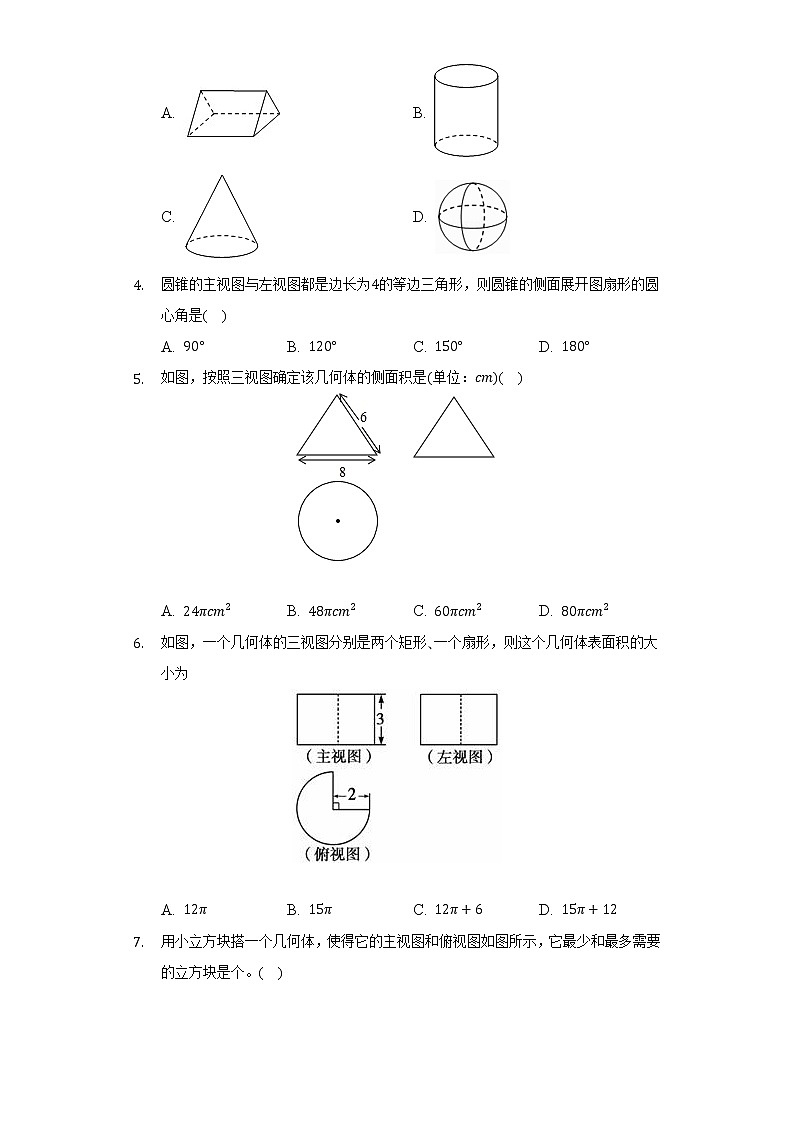
4. 圆锥的主视图与左视图都是边长为的等边三角形，则圆锥的侧面展开图扇形的圆心角是(    )

A.  B.  C.  D.

5. 如图，按照三视图确定该几何体的侧面积是单位：(    )

A.  B.  C.  D.

6. 如图，一个几何体的三视图分别是两个矩形一个扇形，则这个几何体表面积的大小为

A.  B.  C.  D.

7. 用小立方块搭一个几何体，使得它的主视图和俯视图如图所示，它最少和最多需要的立方块是个。(    )

A. 与 B. 与 C. 与 D. 无法确定

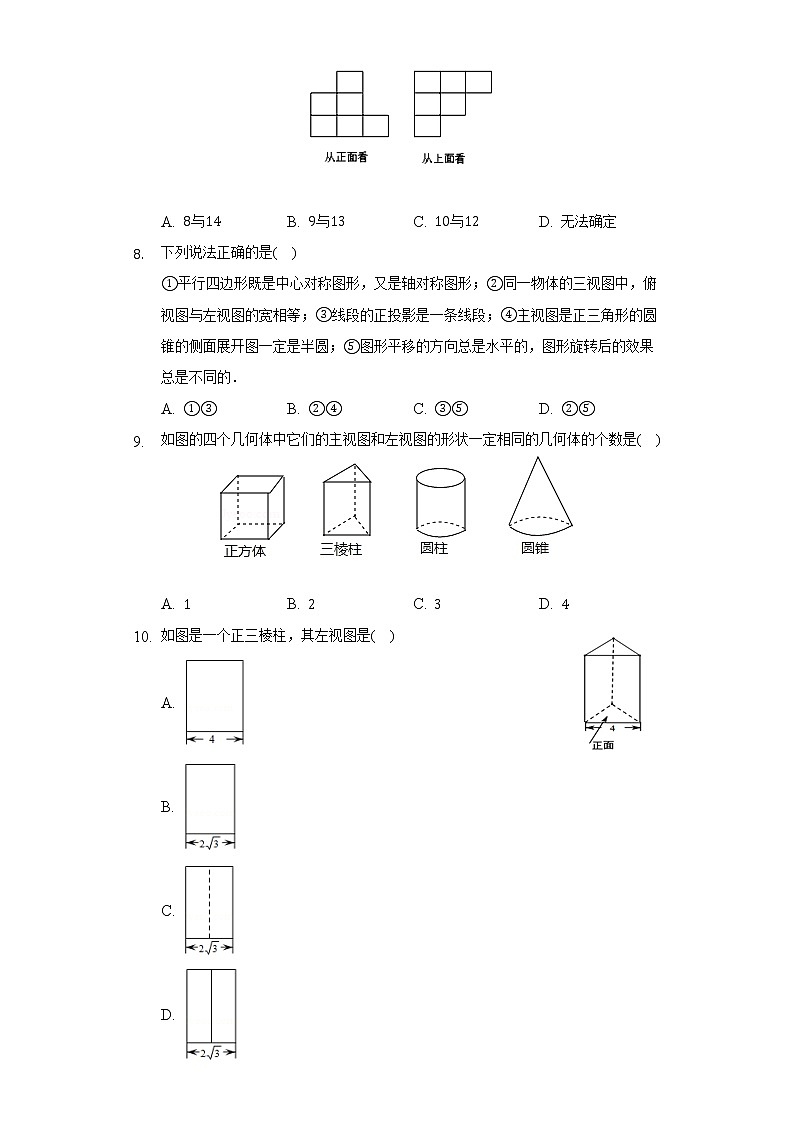
8. 下列说法正确的是(    )

平行四边形既是中心对称图形，又是轴对称图形；同一物体的三视图中，俯视图与左视图的宽相等；线段的正投影是一条线段；主视图是正三角形的圆锥的侧面展开图一定是半圆；图形平移的方向总是水平的，图形旋转后的效果总是不同的．

A.  B.  C.  D.

9. 如图的四个几何体中它们的主视图和左视图的形状一定相同的几何体的个数是(    )

A.  B.  C.  D.

10. 如图是一个正三棱柱，其左视图是(    )

A.
B.
C.
D.

11. 如图是一个长方体的三视图，若其俯视图为正方形，且所有侧面积之和为，现将该长方体的底面边长增加，则新长方体的侧面积之和比原来增加了(    )

A.
B.
C.
D.

12. 如图，数学兴趣小组的小颖想测量教学楼前的一棵树的树高，下午课外活动时她测得一根长为的竹竿的影长是，当她马上测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上如图，他先测得留在墙壁上的影高为，又测得地面的影长为，请你帮她算一下，树高是(    )

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共4小题，共12.0分）

13. 桌上摆着一个由若干个相同正方体组成的几何体，从正面看和从左面看如图所示，这个几何体最多由______个这样的正方体组成．

14. 如图，是一几何体的三视图，根据图中数据，这个几何体的侧面积是________．

15. 如图，已知小华、小强的身高分别为，，小华、小强之间的水平距离为，小华、小强在同一盏路灯下的影长分别为，，则这盏路灯的高度为          

16. 已知某几何体的三视图如图所示，其中俯视图为正六边形，则该几何体的表面积为______．

三、解答题（本大题共8小题，共72.0分）

17. 如图，广场上有两根旗杆，都垂直于地面放置．已知太阳光线与是平行的，经过测量这两根旗杆在太阳光下的影子一样长，那么这两根旗杆的高度相等吗？说说你的理由．

18. 由几个相同的边长为的小立方块搭成的几何体，从上面观察到的形状图如图，格中的数字表示该位置的小立方块的个数．
    请在下面方格纸中分别画出这个几何体从正面和左面看到的形状图．
    
    根据形状图，这个组合几何体的表面积为______个平方单位．包括底面积
    若上述小立方块搭成的几何体从上面看到的形状图不变，各位置的小立方块个数可以改变总数目不变，则搭成这样的组合几何体中的表面积最大是为______个平方单位．包括底面积
19. 如图所示，有张除了正面图案不同，其余都相同的图片．
    
    以上四张图片所示的立体图形中，主视图是矩形的有______；填字母序号
    将这四张图片背面朝上混匀，从中随机抽出一张后放回，混匀后再随机抽出一张．求两次抽出的图片所示的立体图形中，主视图都是矩形的概率．
20. 为了测量“望月阁”的高度，方法如下：如图，小芳在小亮和“望月阁”之间的直线上平放一平面镜，在镜面上做了一个标记，这个标记在直线上的对应位置为点，镜子不动，小亮看着镜面上的标记，他来回走动，走到点时，看到“望月阁”顶端点在镜面中的像与镜面上的标记重合，这时，测得小亮眼睛与地面的高度米，米，然后，在阳光下，他们用测影长的方法进行了第二次测量，方法如下：如图，小亮从点沿方向走了米，到达“望月阁”影子的末端点处，此时，测得小亮身高的影长米，米．如图，已知，，，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中提供的相关信息，求出“望月阁”的高的长度．
     

21. 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如表：

当桌子上放有个碟子时，请写出此时碟子的高度用含的式子表示；
分别从三个方向上看，如图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度．

22. 由几个相同的边长为的小立方块搭成的几何体的俯视图如图，格中的数字表示该位置的小立方块的个数．
    请在下面方格纸图中分别画出这个几何体的主视图和左视图．
    根据三视图，这个组合几何体的表面积为多少个平方单位？包括底面积
    若上述小立方块搭成的几何体的俯视图不变，如图，各位置的小立方块个数可以改变总数目不变，则搭成这样的组合几何体中的表面积最大包括底面积仿照图，将数字填写在图的正方形中．

23. 如图，路灯下，广告标杆的影子是，小明用线段表示的影子是，在处有一棵树，它的影子是．
    
    请在图中画出表示树高的线段．不写作法，保留作图痕迹
    若已知点、到路灯的底部距离相等，小明身高米，影长为米，树的影长是米，请计算树的高度．
24. 街道旁边有一根电线杆和一块半圆形广告牌，有一天，小明突然发现，在太阳光照射下，电线杆的顶端的影子刚好落在半圆形广告牌的最高处，而半圆形广告牌的影子刚好落在地面上一点，已知米，半圆形的直径为米，米．求电线杆的高度．

答案和解析

1.【答案】 

【解析】解：从左面看去，是两个有公共边的矩形，如图所示：

故选：．
找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在视图中．
本题考查了三视图的知识，左视图是从物体的左面看得到的视图．视图中每一个闭合的线框都表示物体上的一个平面，而相连的两个闭合线框常不在一个平面上．
 

2.【答案】 

【解析】

【分析】

本题考查由视图判断几何体；用到的知识点为：俯视图中正方形的个数是组合几何体最底层正方体的个数；组合几何体的最少个数是底层的正方体数加上主视图中第二层和第层正方形的个数．根据该组合体的主视图和俯视图及正方形的个数确定每层的小正方形的个数，然后确定其左视图即可．

【解答】

解：该组合体共有个小正方体，由俯视图和主视图可得
该组合体共有两层，第一层有个小正方体，第二层有三个小正方体，且全位于第二层的最左边和中间，
左视图应该是两层，每层两个，
故选B．

3.【答案】 

【解析】解：三棱柱的主视图为长方形，左视图是三角形，因此选项A符合题意；
圆柱体的主视图、左视图都是长方形，因此选项B不符合题意；
圆锥体的主视图、左视图都是三角形，因此选项C不符合题意；
球体的主视图、左视图包括俯视图都是圆形的，因此选项D不符合题意；
故选：．
分别得出三棱柱、圆柱、圆锥、球体的主视图、左视图，然后进行判断即可．
考查简单几何体的三视图，主视图、左视图、俯视图就是从正面、左面、上面三个方向看所得到的图形．
 

4.【答案】 

【解析】

【分析】
本题综合考查有关扇形和圆锥的相关计算．解题思路：解决此类问题时要紧紧抓住两者之间的两个对应关系：圆锥的母线长等于侧面展开图的扇形半径；圆锥的底面周长等于侧面展开图的扇形弧长．正确对这两个关系的记忆是解题的关键由圆锥的主视图为等边三角形知圆锥的底面圆直径为、侧面展开图扇形的半径为，据此利用弧长公式求解可得．
【解答】
解：圆锥的主视图与左视图都是边长为的等边三角形，
圆锥的母线长为、底面圆的直径为，
则圆锥的侧面展开图扇形的半径为，
设圆锥的侧面展开图扇形的圆心角是，
根据题意，得：，
解得：，
故选：．  

5.【答案】 

【解析】解：由主视图和左视图为三角形判断出是锥体，由俯视图是圆形可判断出这个几何体应该是圆锥；
根据三视图知：该圆锥的母线长为，底面半径为，
故侧面积．
故选：．
由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状，确定圆锥的母线长和底面半径，从而确定其侧面积．
此题考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．
 

6.【答案】 

【解析】

【分析】

本题主要考查由三视图判断几何体，由几何体的三视图得出该几何体是几何体是长方体与三棱柱的组合体，结合图中数据求出组合体的表面积即可．

【解答】

解：由几何体的三视图可得：该几何体是长方体、两个扇形和一个矩形的组合体，该组合体的表面积为：，

故选D．

7.【答案】 

【解析】

【分析】 

本题考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．根据三视图的知识可得，根据主视图和俯视图可得这个几何体共列，再分别求出最少和最多需要的立方块个数即可．

【解答】 

解：如果所需的立方块最少，根据主视图和俯视图可得这个几何体共列，最左边一列有个正方体，中间一列有个正方体，最右边一列有个正方体，共个；

如果所需的立方块最多，根据主视图和俯视图可得，最左边一列有个正方体，中间一列有个正方体，最右边一列有个正方体，共个．

故选B．

8.【答案】 

【解析】

【分析】
本题主要考查了平行四边形的对称性，三视图的特征，平行投影的概念以及图形的基本变换，解题时注意：画物体的三视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等．依据平行四边形的对称性，三视图的特征，平行投影的概念以及图形的基本变换进行判断，即可得到正确结论．
【解答】
解：平行四边形是中心对称图形，不是轴对称图形，故错误；
同一物体的三视图中，俯视图与左视图的宽相等，故正确；
线段的正投影是一条线段或一个点，故错误；
设底面圆的半径为，则圆锥的母线长为，底面周长，
侧面展开图是个扇形，弧长，所以．
所以主视图是正三角形的圆锥的侧面展开图一定是半圆，故正确；
图形平移的方向不一定是水平的，图形旋转后的效果不一定是不同的，故错误．
故选B．  

9.【答案】 

【解析】

【分析】
本题主要考查了简单几何体的三视图．根据主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，分别得到每个几何体的三视图，进而得到答案．
【解答】
解：正方体主视图、左视图都是正方形，故符合题意； 
三棱柱左视图和主视图虽然都是长方形，但是左视图的长方形的宽为三棱柱的底面三角形的高，主视图的长方形的宽为三棱柱的底面三角形的边长，故不符合题意； 
圆柱主视图、左视图都是长方形，故符合题意；
圆锥主视图、左视图都是是三角形，故符合题意 
符合选项的有三个．
故选C．  

10.【答案】 

【解析】解：．
从左边看到的图形是一个宽为的长方形．
故选：．
根据左视图是从左边看到的图形是解答即可．
本题考查简单的几何体的三视图，熟知左视图是从左边看到的图形是解答本题的关键．
 

11.【答案】 

【解析】

【分析】
先求出长方体的底面边长，再求出长方体的棱长，根据长方体的底面边长增加，得到新长方体的底面边长，求出新长方体的侧面积之和，即可得到答案．
此题考查了简单几何体的三视图，整式的混合运算等知识，利用三视图以及勾股定理，得出长方体各部分的长度是解决问题的关键．
【解答】
解：设长方体的底面边长为，
，
，
所有侧面积之和为，
长方体的棱长为：，
长方体的底面边长增加，
新长方体的底面边长为，
新长方体的侧面积之和为：，
，
故选A．  

12.【答案】 

【解析】

【分析】
本题考查了平行投影，解题的关键要知道在同一时刻任何物体的高与其影子的比值是相同的，利用这个结论可以求出树高．
【解答】
解：如图，设是在地面的影子，树高为，








根据竹竿的高与其影子的比值和树高与其影子的比值相同得
而，
，
树在地面的实际影子长是，
再竹竿的高与其影子的比值和树高与其影子的比值相同得
，
，
树高是．
故选A．  

13.【答案】 

【解析】解：由主视图可得组合几何体有列，由左视图可得组合几何体有行，
最底层几何体最多正方体的个数为：，
由主视图和左视图可得第二层个角各有一个正方体，
第二层共有个正方体，
该组合几何体最多共有个正方体．
故答案为：．
由主视图可得组合几何体有列，由左视图可得组合几何体有行，可得最底层几何体最多正方体的个数；由主视图和左视图可得第二层个角各有一个正方体，相加可得所求．
此题考查由视图判断几何体；得到最底层正方体的最多的个数是解决本题的突破点；用到的知识点为：最底层正方体的最多的个数行数列数．
 

14.【答案】 

【解析】

【分析】
本题考查了由三视图判断几何体、圆锥的计算以及勾股定理，由几何体的三视图可得出原几何体为圆锥是解题的关键．由几何体的三视图可得出原几何体为圆锥，根据图中给定数据求出母线的长度，再套用侧面积公式即可得出结论．
【解答】
解：由三视图可知，原几何体为圆锥，
，
．
故答案为．  

15.【答案】 

【解析】解：如图，，
∽，∽，
，，
即，，
解得：，
故答案为：．
作出图形，得到相似三角形，利用相似三角形对应边的比相等列式计算即可求解．
本题考查的是相似三角形的应用，相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
 

16.【答案】 

【解析】解：观察该几何体的三视图发现该几何体为正六棱柱，其底面边长为，高为，
故其边心距为，
所以其表面积为，
故答案为：．
观察该几何体的三视图发现该几何体为正六棱柱，然后根据提供的尺寸求得其表面积即可．
本题考查了由三视图判断几何体的知识，解题的关键是能够根据三视图判断几何体的形状及各部分的尺寸，难度不大．
 

17.【答案】解：两根旗杆的高度相等．
理由如下：太阳光线与是平行，
，
两根旗杆都垂直于地面放置，
，
两根旗杆在太阳光下的影子一样长，
，
在和中，，
≌，
，
即两根旗杆的高度相等． 

【解析】根据平行投影可得，再根据垂直可得，然后利用“角边角”证明和全等，根据全等三角形对应边相等即可得证．
本题考查了全等三角形的应用，根据题意找出三角形全等的条件，然后证明两三角形全等是解题的关键．
 

18.【答案】解：如图所示：

根据从三个方向看的形状图，这个几何体的表面积为平方单位．
故答案为：；
要使表面积最大，则需满足两正方体重合的最少，此时从上面看得到的形状图为：

这样上面共有个小正方形，下面共有个小正方形；左面共有个小正方形，右面共有个正方形；前面共有个小正方形，后面共有个正方形，
表面积为：平方单位．
故答案为：． 

【解析】主视图有列，每列小正方形数目分别为，；左视图有列，每列小正方形数目分别为，；
上面共有个小正方形，下面共有个小正方形；左面共有个小正方形，右面共有个小正方形；前面共有个小正方形，后面共有个小正方形，继而可得出表面积．
要使表面积最大，则需满足两正方体重合的最少，画出从上面看得到的形状图，计算表面积即可．
 

19.【答案】， 

【解析】解：球的主视图为圆；
长方体的主视图是矩形；
圆锥的主视图为等腰三角形；
圆柱的主视图为矩形，
故答案为：，；     

解：列表可得

分
由表可知，共有种等可能结果，其中两次抽出的图片所示立体图形的主视图都是矩形的有种，分别是，，，，所以两次抽出的图片所示立体图形的主视图都是矩形的概率为，即．
分别写出每个几何体的主视图，然后即可确定答案；
列表后将所有等可能的结果列举出来，利用概率公式求解即可；
本题考查了由三视图判断几何体、概率的计算公式等知识，解题的关键是能够写出每个几何体的主视图及利用列表法将等可能的所有结果列举出来，难度不大．
 

20.【答案】解：由题意可得：，
，，
故∽，∽，
则，，
即：：，：：，
解得：，
答：“望月阁”的高的长度为． 

【解析】此题主要考查了相似三角形的判定与性质，正确利用已知得出相似三角形是解题关键．根据镜面反射原理结合相似三角形的判定方法得出∽，∽，进而利用相似三角形的性质得出的长．
 

21.【答案】解：由题意得：；
由三视图可知共有个碟子，
叠成一摞的高度，
答：叠成一摞后的高度为． 

【解析】此题考查了图形的变化类问题及由三视图判断几何体的知识，解题的关键是具有获取信息读表、分析问题解决问题的能力．找出碟子个数与碟子高度的之间的关系式是此题的关键．
由表中给出的碟子个数与碟子高度的规律，可以看出碟子数为时，碟子的高度为；
根据三视图得出碟子的总数，由知每个碟子的高度，即可得出答案．
 

22.【答案】解：这个几何体的主视图和左视图如图所示：
俯视图知：上面共有个小正方形，下面共有个小正方形；
由左视图知：左面共有个小正方形，右面共有个正方形；
由主视图知：前面共有个小正方形，后面共有个正方形，
故可得表面积为：；
要使表面积最大，则需满足两正方体重合的最少，此时俯视图为： 

【解析】从正面看到的图形是两列，第一列有两个正方形，第二列有三个正方形；从左面看有两列，第一列有三个正方形，第二列有一个正方形．
根据三视图可以求出表面积，
要使表面积最大，则需满足两正方体重合的最少，将其中的两个位置各放个，其余都放在剩下的位置上即可．
考查简单几何体的三视图，从三个方向看物体的形状实际就是从三个方向的正投影所得到的图形．
 

23.【答案】解：如图所示：


点、到路灯的底部距离相等，
，
，，
，
∽，
小明身高米，影长为米，树的影长是米，
，即，解得米． 

【解析】根据中心投影的特点可知，连接物体和它影子的顶端所形成的直线必定经过点光源．所以分别把和的顶端和影子的顶端连接并延长可交于一点，即点光源的位置，从而可确定大树高的线段．
根据题意得出∽，再根据相似三角形的对应边成比例即可得出的长．
本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．
 

24.【答案】解：连接，过点作于，则是矩形．
，，
，．
是的切线，

．
太阳光线是平行光线，
，
又，
．
又，
∽，
，即，
解得：．
即，
答：电线杆的高度为米． 

【解析】连接，过点作于，根据勾股定理以及相似三角形的性质进行计算．
此题主要考查了相似三角形的应用，熟练运用勾股定理以及相似三角形的判定和性质是解题关键．