数学必修 第一册3.4 函数的应用（一）教案及反思

 《3.4函数的应用（一）》

  教学设计 

一．教材分析

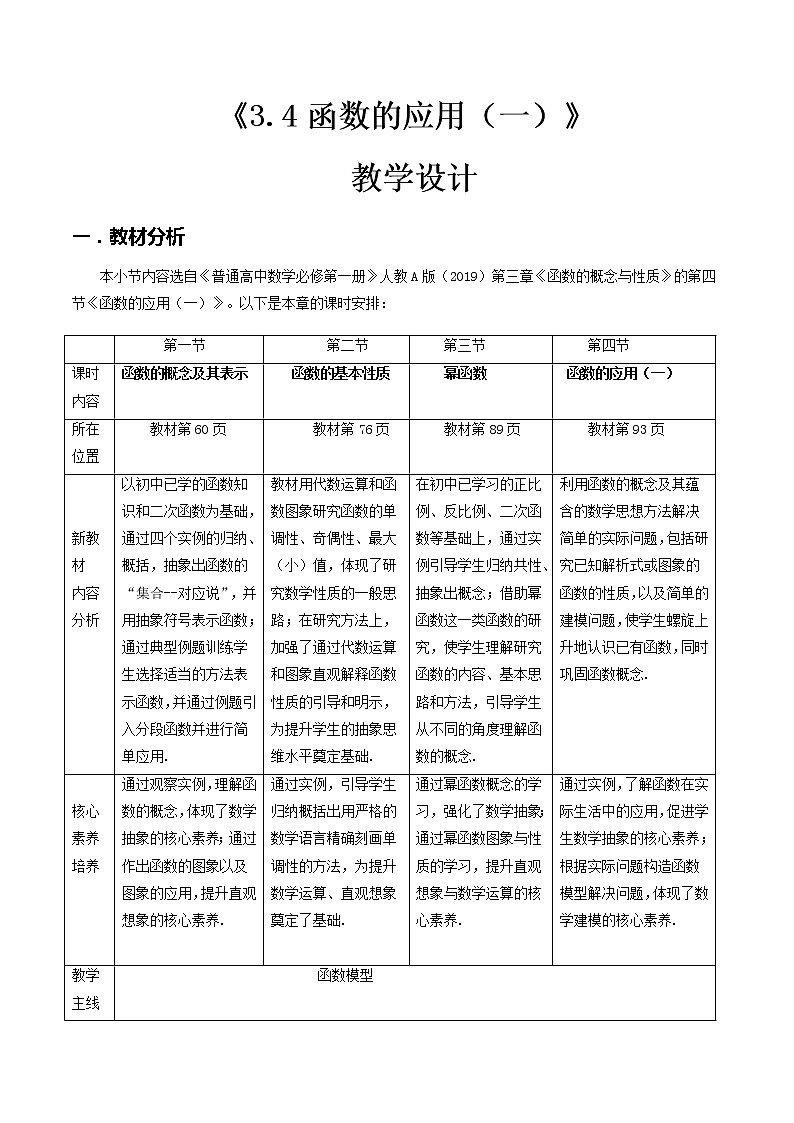
本小节内容选自《普通高中数学必修第一册》人教A版（2019）第三章《函数的概念与性质》的第四节《函数的应用（一）》。以下是本章的课时安排：

二，学情分析

    通过前面函数知识的学习，学生在知识上已经具备了一定的知识经验和基础，初步具备运用函数思想解决问题的能力，但是解题意识和思维的深刻性有待进一步加强，在探究问题的能力以及合作交流方面的发展不均衡，需要教师创设和谐平等的课堂气氛，加以调动。

三．学习目标

1、能够找出简单实际问题中的函数关系式，初步体会应用一次函数、二次函数、分段函数模型解决实际问题，培养数学建模的核心素养。

2、运用一次函数、二次函数、分段函数模型解决实际应用中的问题，提升数学运算的核心素养。

四．教学重点

重点：运用一次函数、二次函数、分段函数模型的处理实际问题；

难点：运用函数思想理解和处理现实生活和社会中的简单问题．

五．教学过程

（一）新知导入

1. 创设情境，生成问题

某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天多售出2件．于是商场经理决定每件衬衫降价15元．那么经理的决定正确吗？

2.探索交流，解决问题

【探究1】解答函数实际应用问题时,一般要分哪四步进行?

【提示】第一步:分析、联想、转化、抽象;

第二步:建立函数模型,把实际应用问题转化为数学问题;

第三步:解答数学问题,求得结果;

第四步:把数学结果转译成具体问题的结论,做出解答.

而这四步中,最为关键的是把第二步处理好.只要把函数模型建立妥当,所有的问题即可在此基础上迎刃而解.

【设计意图】通过探究，引导学生尝试用函数的知识解决实际应用问题，提高学生思考并解决问题的能力。

（二） 函数的应用

1.一次函数模型的应用

例1.为了发展电信事业，方便用户，电信公司对移动电话采用不同的收费方式，其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间x(分)与通话费用y(元)的关系如图所示．

(1)分别求出通话费用y1，y2与通话时间x之间的函数解析式；

(2)请帮助用户计算在一个月内使用哪种卡便宜．

[解析]　(1)由图象可设y1＝k1x＋29，y2＝k2x，把点B(30,35)，C(30,15)分别代入y1＝k1x＋29，y2＝k2x，得k1＝，k2＝.

∴y1＝x＋29(x≥0)，y2＝x(x≥0)．

(2)令y1＝y2，即x＋29＝x，则x＝96.

当x＝96时，y1＝y2，两种卡收费一致；

当x＜96时，y1＞y2，使用便民卡便宜；

当x＞96时，y1＜y2，使用如意卡便宜.

【类题通法】1.一次函数模型解决实际问题的原则

一次函数模型的应用层次要求不高，一般情况下按照“问什么，设什么，列什么”的原则来处理，求解过程也比较简单.

2.一次函数模型解决问题的注意点

用一次函数模型解决实际问题时，对于给出图象的应用题可先结合图象利用待定系数法求出解析式．对于一次函数y＝ax＋b(a≠0)，当a＞0时为增函数，当a＜0时为减函数．另外，要结合题目理解(0，b)或这些特殊点的意义.

【巩固练习1】某公司市场营销人员的个人月收入与其每月的销售量成一次函数关系，其图象如图所示，由图中给出的信息可知，营销人员没有销售量的收入是(　　)

A．310元   B．300元

C．290元   D．280元

解析　设y＝kx＋b(k≠0)，代入(1,800)和(2,1 300)，

则得

所以y＝500x＋300，当x＝0时，y＝300.

答案　B

2.二次函数模型的应用

例2.某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y＝－48x＋8 000，已知此生产线年产量最大为210吨．若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？

[解析]　设可获得总利润为R(x)万元，

则R(x)＝40x－y＝40x－＋48x－8 000

＝－＋88x－8 000

＝－(x－220)2＋1 680,0≤x≤210.

∵R(x)在[0,210]上是增函数，

∴当x＝210时，

R(x)max＝－(210－220)2＋1 680＝1 660(万元)．

∴年产量为210吨时，可获得最大利润1 660万元．

【类题通法】二次函数模型的应用

构建二次函数模型解决最优问题时,可以利用配方法、判别式法、换元法、讨论函数的单调性等方法求最值,也可以根据函数图象的对称轴与函数定义域的对应区间之间的位置关系讨论求解,但一定要注意自变量的取值范围.

【巩固练习2】某桶装水经营部每天的房租、人员工资等固定成本为200元，每桶水的进价是5元，销售单价与日均销售量的关系如表所示.

请根据以上数据作出分析，这个经营部怎样定价才能获得最大利润？

[解析]　由表中数据可知，销售单价每增加1元，日均销售量就减少40桶，

设在进价的基础上增加x元后，日均销售利润为y元，

在此情况下的日均销售量为480－40(x－1)＝(520－40x)(桶)．

令520－40x>0，则0<x<13.

y＝(520－40x)x－200＝－40x2＋520x－200

＝－40(x－6.5)2＋1 490,0<x<13.

易知，当x＝6.5时，y有最大值．

所以只需将销售单价定为11.5元，就可获得最大利润．

3.分段函数模型的应用

例3.某公司生产某种电子仪器的固定成本为20 000元，每生产一台仪器需增加投入100元，已知总收益满足函数：R(x)＝

(1)将利润表示为月产量的函数f(x)；

(2)当月产量为何值时，公司所获利润最大？最大利润为多少元？(总收益＝总成本＋利润)

[解析]　(1)设月产量为x台，则总成本为(20 000＋100x)元，从而

f(x)＝

(2)当0≤x≤400时，f(x)＝－(x－300)2＋25 000，

∴当x＝300时，有最大值25 000；

当x>400时，f(x)＝60 000－100x是减函数，

f(x)<60 000－100×400<25 000.

∴当x＝300时，f(x)的最大值为25 000.

即每月生产300台仪器时，利润最大，最大利润为25 000元．

【类题通法】1.分段函数的“段”一定要分得合理,不重不漏.

2.分段函数的定义域为对应每一段自变量取值范围的并集.

3.分段函数的值域求法:逐段求函数值的范围,最后比较再下结论.

【巩固练习3】某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元．

(1)当一次订购量为多少个时，零件的实际出厂单价恰降为51元？

(2)设一次订购量为x个时，零件的实际出厂单价为P元，写出函数P＝f(x)的表达式；

(3)当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1 000个时，利润又是多少元？(工厂售出一个零件的利润＝实际出厂单价－成本)

[解析]　(1)设每个零件的实际出厂单价恰好降为51元时，一次订购量为x0个，则

x0＝100＋＝550.

因此，当一次订购量为550个时，每个零件的实际出厂价格恰好降为51元．

(2)当0＜x≤100时，P＝60.

当100＜x<550时，P＝60－0.02(x－100)＝62－.

当x≥550时，P＝51，

∴P＝f(x)＝

(3)设销售商的一次订购量为x个时，工厂获得的利润为L元，则L＝(P－40)x

＝

当x＝500时，L＝6 000；当x＝1 000时，L＝11 000.

因此，当销售商一次订购500个零件时，该厂获得的利润是6 000元；如果订购1 000个时，利润是11 000元．

【设计意图】通过例题学习，使学生初步体会一次函数、二次函数、幂函数、分段函数模型的广泛应用，能运用函数思想处理现实生活中的简单应用问题．

（三）操作演练  素养提升

1.某厂日产手套总成本y(元)与手套日产量x(副)的关系式为y＝5x＋4 000，而手套出厂价格为每副10元，则该厂为了不亏本，日产手套至少为(　　)

A．200副　　　　　 B．400副

C．600副  D．800副

2.拟定从甲地到乙地通话m分钟的电话费f(m)＝1.06(0.50×[m]＋1)，其中m>0，[m]是大于或等于m的最小整数(如[3]＝3，[3.7]＝4，[5.1]＝6)．则从甲到乙地通话时间为5.5分钟的通话费为(　　)

A．3.71  B．3.97

C．4.24  D．4.77

3．用长度为24 m的材料围成一个矩形家禽养殖场，中间加两道隔墙，要使矩形面积最大，隔墙长度应为(　　)

A．3 m  B．4 m

C．5 m  D．6 m

4.随着海拔高度的升高，大气压强下降，空气中的含氧量也随之下降，且含氧量y(g/m3)与大气压强x(kPa)成正比例函数关系．当x＝36 kPa时，y＝108 g/m3，则y与x的函数关系式为(　　)

A．y＝3x(x≥0)   B．y＝3x

C．y＝x(x≥0)   D．y＝x

答案：1.D   2.C   3.A    4.A

【设计意图】通过练习巩固本节所学知识，通过学生解决问题的能力，感悟其中蕴含的数学思想，增强学生的应用意识。

（四）课堂小结，反思感悟

 1.知识总结：

2.学生反思：

（1）通过这节课，你学到了什么知识？

（2）在解决问题时，用到了哪些数学思想？

【设计意图】

通过总结，让学生进一步巩固函数的应用，树立用函数模型解决实际问题的意识。

六．布置作业

完成教材：第95页  练习     第1，2,3题

          第95 页   习题3.4  第1,2,3,4,5题