人教A版 (2019)必修 第一册5.5 三角恒等变换第2课时教案

这是一份人教A版 (2019)必修 第一册5.5 三角恒等变换第2课时教案，共14页。教案主要包含了教材分析，学情分析，学习目标，教学重点，教学过程，布置作业等内容，欢迎下载使用。

教学设计
一、教材分析
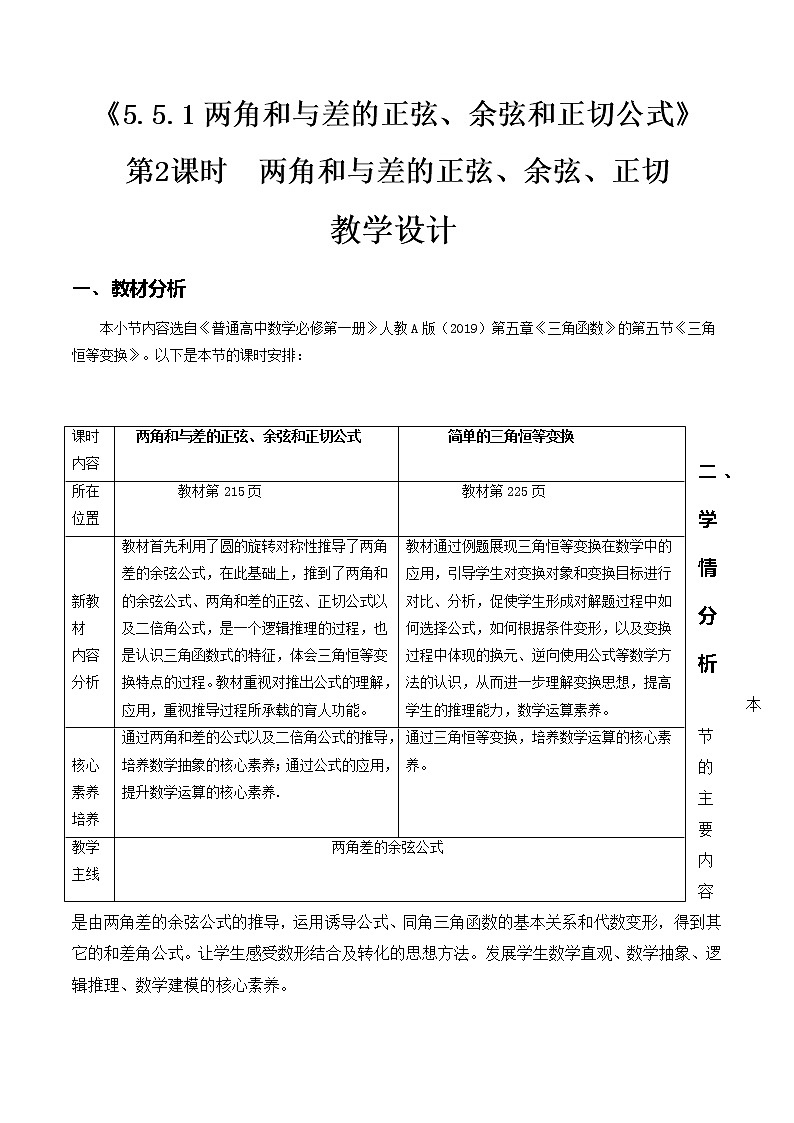
本小节内容选自《普通高中数学必修第一册》人教A版（2019）第五章《三角函数》的第五节《三角恒等变换》。以下是本节的课时安排：
二、学情分析
本节的主要内容是由两角差的余弦公式的推导，运用诱导公式、同角三角函数的基本关系和代数变形，得到其它的和差角公式。让学生感受数形结合及转化的思想方法。发展学生数学直观、数学抽象、逻辑推理、数学建模的核心素养。
三、学习目标
1.掌握由两角差的余弦公式推导出两角和的余弦公式及两角和与差的正弦、正切公式,培养数学抽象的核心素养；
2. 熟悉两角和与差的正弦、余弦、正切公式的灵活运用，了解公式的正用、逆用以及角的变换的常用方法，提升数学运算的核心素养。
四、教学重点
重点：两角和与差的正弦、余弦、正切公式的探究及公式之间的内在联系；
难点：求值过程中角的范围分析及角的变换.
五、教学过程
（一）新知导入
1. 创设情境，生成问题
坐在教室里，需要一个合适视角才能看清楚黑板；在足球比赛中，若你从所守球门附近带球过人沿直线推进，要想把球准确地踢进大门去，需要确定一个最佳位置，这些实际生活中的问题可不是仅仅一个角度就可以解决的，其中涉及到至少两个角度的因素，只有把问题分析全面，才能稳操胜券．
怎样确定两角之间的关系呢？
（二）两角和与差的正弦、余弦、正切公式
【探究1】由公式 csα−β出发 ， 你能推导出两角和的余弦公式吗？
【提示】 在公式C(α－β)中，令－β代替β，则有cs(α＋β)＝
cs αcs(－β)＋sin αsin(－β)＝cs αcs β－sin αsin β.
即cs(α＋β)＝cs αcs β－sin αsin β.(C(α＋β))
两角和的余弦公式：
csα+β=csαcsβ−sinαsinβ．简记作 C（α ＋ β ） ．
【做一做1】求cs 105°的值。
【解析】原式＝cs(60°＋45°)＝cs 60°cs 45°－sin 60°sin 45°＝eq \f(1,2)×eq \f(\r(2),2)－eq \f(\r(3),2)×eq \f(\r(2),2)＝eq \f(\r(2)－\r(6),4).
【探究2】用诱导公式五 （ 或六 ） 可以实现正弦 、 余弦的互化 ． 你能根据 Ｃ （α ＋ β ） ， Ｃ （ α － β ） 及诱导公式五 （ 或六 ）， 推导出用任意角α ， β 的正弦 、 余弦表示 sin （ α ＋ β ）， sin（ α － β ） 的公式吗 ？
【提示】运用C(α＋β)和诱导公式，有
sin(α＋β)＝cseq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)－α＋β))＝cseq \b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))－β))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))cs β＋sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))sin β＝sin αcs β＋cs αsin β.
即sin(α＋β)＝sin αcs β＋cs αsin β.(S(α＋β))
在公式S(α＋β)中用－β代替β，可以得到sin(α－β)＝sin αcs(－β)＋cs αsin(－β)＝sin αcs β－cs αsin β.
即sin(α－β)＝sin αcs β－cs αsin β.(S(α－β))
两角和差的正弦公式：
sinα+β ＝ sinαcsβ+csαsinβ，（ S（α ＋ β ） ）
sinα−β ＝ sinαcsβ−csαsinβ ; （ S（α － β ） ）
（1）两角和差的正、余弦公式的理解及其结构特点
①公式中的α,β均为任意角;
②两角和与差的正、余弦公式可以看成是诱导公式的推广,诱导公式可以看成是两角和与差的正、余弦公式的特例;
③两角和与差的正弦公式结构是“正余余正,加减相同”,两角和与差的余弦公式结构是“余余正正,加减相反”.
(2)两角和与差的正弦公式的一般使用方法
①正用:把sin(α±β)从左向右展开;
②逆用:公式的右边化简成左边的形式,当结构不具备条件时,要用相关公式调节后再逆用.
③变形应用:它涉及两个方面,一是公式本身的变形;二是角的变形,也称为角的拆分变换,如β=(α+β)-α,2α=(α+β)+(α-β).
【做一做2】已知cs α＝eq \f(1,3)，α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，sin β＝－eq \f(3,5)，β是第三象限角．求sin(α＋β)，sin(α－β)的值；
【解析】∵cs α＝eq \f(1,3)，α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，∴sin α＝eq \r(1－cs2α)＝eq \f(2,3)eq \r(2).
∵sin β＝－eq \f(3,5)，β是第三象限角，∴cs β＝－eq \r(1－sin2β)＝－eq \f(4,5).
∴sin(α＋β)＝sin αcs β＋cs αsin β＝eq \f(2,3)eq \r(2)×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4,5)))＋eq \f(1,3)×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,5)))＝－eq \f(3＋8\r(2),15).
sin(α－β)＝sin αcs β－cs αsin β＝eq \f(2,3)eq \r(2)×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4,5)))－eq \f(1,3)×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,5)))＝eq \f(3－8\r(2),15).
【重要结论】
对于形如asin x＋bcs x(a，b不同时为零)的式子可以引入辅助角变形为Asin(x＋φ)的形式．
基本思路是逆用和角的正弦公式，把它化成Asin(x＋φ)的形式，即
asin x＋bcs x＝eq \r(a2＋b2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(a,\r(a2＋b2))sin x＋\f(b,\r(a2＋b2))cs x)).
令cs φ＝eq \f(a,\r(a2＋b2))，sin φ＝eq \f(b,\r(a2＋b2))，则
原式＝eq \r(a2＋b2)(sin xcs φ＋cs xsin φ)＝eq \r(a2＋b2)sin(x＋φ)，其中tan φ＝eq \f(b,a).
【做一做3】sin x＋cs x＝eq \r(2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)sin x＋\f(\r(2),2)cs x))＝eq \r(2)eq \b\lc\(\rc\)(\a\vs4\al\c1(sin xcs \f(π,4)＋cs xsin \f(π,4)))＝eq \r(2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4))).
【探究3】 你能根据正切函数与正弦函数 、 余弦函数的关系 ， 从 Ｃ(α ± β ) ， Ｓ( α ± β ) 出发 ， 推导出用任意角 α ， β 的正切表示 tanα+β ， tanα−β 的公式吗 ？
【提示】当cs(α＋β)≠0时，将公式S(α＋β)，C(α＋β)的两边分别相除，有
tan(α＋β)＝eq \f(sinα＋β,csα＋β)＝eq \f(sin αcs β＋cs αsin β,cs αcs β－sin αsin β).
当cs αcs β≠0时，将上式的分子、分母分别除以cs α·cs β，得
tan(α＋β)＝eq \f(tanα＋tan β,1－tan αtan β).(T(α＋β))
由于tan(－β)＝eq \f(sin－β,cs－β)＝eq \f(－sin β,cs β)＝－tan β.
在T(α＋β)中以－β代替β，可得tan(α－β)＝eq \f(tan α＋tan －β,1－tan αtan－β)＝eq \f(tan α－tan β,1＋tan αtan β).
即tan(α－β)＝eq \f(tanα－tan β,1＋tan αtan β).(T(α－β))
【探究4】公式中α，β为任意实数吗？
【提示】 不是，α，β，α＋β≠kπ＋eq \f(π,2)，k∈Z.
两角和差的正切公式： tanα+β = tanα+tanβ 1− tanαtanβ T(α + β )
tanα−β = tanα−tanβ 1+ tanαtanβ T(α − β )
【做一做4】已知，，则 ．
【解析】因为，，所以．
【答案】
【变形公式】T(α±β)可变形为如下形式：
①tan α±tan β＝tan(α±β)(1∓tan αtan β)或②1∓tan αtan β＝eq \f(tan α±tan β,tanα±β).
当α±β为特殊角时，常考虑使用变形①，遇到1与切的乘积的和(或差)时常用变形②.
【做一做5】 若α＋β＝eq \f(π,4)，求(1＋tan α)(1＋tan β)的值．
【解析】 (1＋tan α)(1＋tan β)＝1＋tan α＋tan β＋tan α·tan β.
又∵α＋β＝eq \f(π,4)，∴tan(α＋β)＝eq \f(tan α＋tan β,1－tan αtan β)＝1，
∴tan α＋tan β＝1－tan α·tan β，
∴tan α＋tan β＋tan α·tan β＝1，
∴(1＋tan α)(1＋tan β)＝1＋1＝2.
公式 Ｓ (α ＋ β ) ， Ｃ(α ＋ β ) ， Ｔ(α ＋ β ) 给出了任意角 α ， β 的三角函数值与其和角 α ＋ β 的三角函数值之间的关系 ． 为方便起见 ， 我们把这三个公式都叫做 和角公式 ．
类似地 ， Ｓ(α － β ) ， Ｃ(α － β ) ， Ｔ(α － β )都叫做 差角公式 ．
C(α－β)、C(α＋β)、S(α－β)、S(α＋β)、T(α－β)、T(α＋β)之间可以利用换角、诱导公式、同角关系式推导而来，其最基本公式为C(α－β)．
它们之间的关系为：
（三）典型例题
1.给角求值
例1. 求值：(1)sin 14°cs 16°＋sin 76°cs 74°；
(2)sin eq \f(π,12)－eq \r(3)cs eq \f(π,12)；
(3)eq \f(1＋tan 75°,1－tan 75°).
【解析】(1)原式＝sin 14°cs 16°＋sin(90°－14°)cs(90°－16°)＝sin 14°cs 16°＋cs 14°sin 16°
＝sin(14°＋16°)＝sin 30° ＝eq \f(1,2).
(2)法一：原式＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin \f(π,12)－\f(\r(3),2)cs \f(π,12)))＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(sin \f(π,6)sin \f(π,12)－cs \f(π,6)cs \f(π,12)))
＝－2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)＋\f(π,12)))＝－2cs eq \f(π,4)＝－eq \r(2).
法二：原式＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin \f(π,12)－\f(\r(3),2)cs \f(π,12)))＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(cs \f(π,3)sin \f(π,12)－sin \f(π,3)cs \f(π,12)))
＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)－\f(π,3)))＝－2sin eq \f(π,4)＝－eq \r(2).
(3)原式＝eq \f(tan 45°＋tan 75°,1－tan 45°tan 75°)＝tan(45°＋75°)＝tan 120°＝－eq \r(3).
【类题通法】给角求值，其中角一般为非特殊角，求值时将非特殊角转化为特殊角，或者通过化简结合公式正用、逆用、变形用求值；
提醒:在逆用两角的和与差的正弦和余弦公式时,首先要注意结构是否符合公式特点,其次注意角是否满足要求.
【巩固练习1】求下列各式的值．
(1)sin 347°cs 148°＋sin 77°cs 58°；
(2)eq \r(3)sin eq \f(π,12)＋cs eq \f(π,12)；
(3)tan 10°＋tan 50°＋eq \r(3)tan 10°tan 50°.
【解析】(1)原式＝sin(360°－13°)cs(180°－32°)＋sin(90°－13°)·cs(90°－32°)
＝sin 13°cs 32°＋cs 13°sin 32°＝sin(13°＋32°)＝sin 45°＝eq \f(\r(2),2).
(2)原式＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)sin \f(π,12)＋\f(1,2)cs \f(π,12)))＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(sin \f(π,12)cs \f(π,6)＋sin \f(π,6)cs \f(π,12)))
＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)＋\f(π,6)))＝2sin eq \f(π,4)＝eq \r(2).
(3)∵tan 60°＝tan(10°＋50°)＝eq \f(tan 10°＋tan 50°,1－tan 10°tan 50°)，
∴tan 10°＋tan 50°＝tan 60°(1－tan 10°tan 50°)，
∴原式＝tan 60°(1－tan 10°tan 50°)＋eq \r(3)tan 10°tan 50°
＝eq \r(3)－eq \r(3)tan 10°tan 50°＋eq \r(3)tan 10°tan 50°＝eq \r(3).
2.给值求值
例2. 已知eq \f(π,4)<β<α【解析】∵eq \f(π,4)<β<α又∵sin(α＋β)＝－eq \f(3,5)，∴π<α＋β∵cs(α－β)＝eq \f(12,13)，∴sin(α－β)＝eq \f(5,13).
∴sin 2α＝sin[(α＋β)＋(α－β)]＝sin(α＋β)cs(α－β)＋cs(α＋β)sin(α－β)
＝－eq \f(3,5)×eq \f(12,13)＋eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4,5)))×eq \f(5,13)＝－eq \f(56,65).
【类题通法】解此类问题的关键是把“所求角”用“已知角”表示出来．①当“已知角”有两个时，“所求角”一般表示为两个“已知角”的和或差的形式，如本题．②当“已知角”有一个时，此时应着眼于“所求角”与“已知角”的关系，然后应用诱导公式把“所求角”变成“已知角”．③角的拆分方法不唯一，可根据题目合理地选择拆分方式．如α＝(α＋β)－β＝β－(β－α)，α＝eq \f(α＋β,2)＋eq \f(α－β,2)，β＝eq \f(α＋β,2)－eq \f(α－β,2)，2α＝(α＋β)＋(α－β)，2β＝(α＋β)－(α－β)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)＋α))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)＋β))＝eq \f(π,2)＋(α＋β)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)＋α))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－β))＝eq \f(π,2)＋(α－β)．
【巩固练习2】已知tan(α＋β)＝eq \f(3,5)，taneq \b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,3)))＝eq \f(1,3)，求taneq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,3)))的值．
【解析】 taneq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,3)))＝taneq \b\lc\[\rc\](\a\vs4\al\c1(α＋β－\b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,3)))))＝eq \f(tanα＋β－tan\b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,3))),1＋tanα＋βtan\b\lc\(\rc\)(\a\vs4\al\c1(β－\f(π,3)))) ＝eq \f(\f(3,5)－\f(1,3),1＋\f(3,5)×\f(1,3))＝eq \f(2,9).
3.辅助角公式的应用
例3.(1)当－eq \f(π,2)≤x≤eq \f(π,2)时，函数f(x)＝sin x＋eq \r(3)cs x的最大值为________，最小值为________．
(2)函数y＝eq \f(\r(2),4)sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－x))＋eq \f(\r(6),4)cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－x)).的最小正周期是________．
【解析】 (1)f(x)＝sin x＋eq \r(3)cs x＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin x＋\f(\r(3),2)cs x))＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(sin xcs \f(π,3)＋cs xsin \f(π,3)))＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3))).
∵－eq \f(π,2)≤x≤eq \f(π,2)，∴－eq \f(π,6)≤x＋eq \f(π,3)≤eq \f(5,6)π，∴－eq \f(1,2)≤sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))≤1，即－1≤f(x)≤2.
(2)∵y＝eq \f(\r(2),2)eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,2)sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－x＋\f(\r(3),2)cs\f(π,4)－x))))
＝eq \f(\r(2),2)eq \b\lc\[\rc\](\a\vs4\al\c1(sin \f(π,6)sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－x))＋cs \f(π,6)cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－x))))
＝eq \f(\r(2),2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－x－\f(π,6)))＝eq \f(\r(2),2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)－x))＝eq \f(\r(2),2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(5π,12))).
∴T＝2π
【答案】(1) 2 －1 (2)2π
【类题通法】对于形如asin x＋bcs x(a，b不同时为零)的式子可以引入辅助角变形为Asin(x＋φ)的形式．
【巩固练习3】化简：(1)eq \r(2)(cs x－sin x)；
(2)3eq \r(15)sin x＋3eq \r(5)cs x.
【解析】 (1)eq \r(2)(cs x－sin x)＝eq \r(2)×eq \r(2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)cs x－\f(\r(2),2)sin x))
＝2(cs eq \f(π,4)cs x－sin eq \f(π,4)sin x)＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)＋x)).
(2)3eq \r(15)sin x＋3eq \r(5)cs x＝6eq \r(5)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)sin x＋\f(1,2)cs x))
＝6eq \r(5)eq \b\lc\(\rc\)(\a\vs4\al\c1(sin \f(π,3)sin x＋cs \f(π,3)cs x))＝6eq \r(5)cseq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3))).
4.给值求角
例4.已知sin α＝eq \f(\r(5),5)，sin β＝eq \f(\r(10),10)，且α，β为锐角，求α＋β的值．
【解析】∵sin α＝eq \f(\r(5),5)，α为锐角，∴cs α＝eq \r(1－sin2α)＝eq \f(2,5)eq \r(5).
又sin β＝eq \f(\r(10),10)，β为锐角，∴cs β＝eq \r(1－sin2β)＝eq \f(3,10)eq \r(10).
∴cs(α＋β)＝cs αcs β－sin αsin β＝eq \f(2\r(5),5)×eq \f(3\r(10),10)－eq \f(\r(5),5)×eq \f(\r(10),10)＝eq \f(\r(2),2).
又α、β∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，∴0<α＋β<π，因此α＋β＝eq \f(π,4).
【探究】若把本例题的过程改为求 sin(α+β)，如何求角 α＋β 的大小．
【解析】由sin(α＋β)＝sin αcs β+csαsin β
＝
∵sin α＝55<22，α为锐角,∴α∈(0,π4), 又sin β＝1010<22，β为锐角，∴β∈(0,π4 )
∴α+β∈(0,π2 )∴α+β＝π4 .
【类题通法】1．求解该类问题常犯的错误是对角的范围讨论程度过大(小)，导致求出的角不合题意或者漏解．
2．求角的大小，要解决两点：(1)确定所求角的范围，(2)求角的某一三角函数值，特别是要根据角的范围确定取该角的哪一种三角函数值,正弦、余弦、正切的选取原则是：
【巩固练习4】已知tan(α－β)＝eq \f(1,2)，tan β＝－eq \f(1,7)，且α，β∈(0，π)，求2α－β的值．
【解析】 tan α＝tan[(α－β)＋β]＝eq \f(tanα－β＋tan β,1－tanα－βtan β)＝eq \f(1,3)>0.而α∈(0，π)，故α∈(0，eq \f(π,2))．
∵tan β＝－eq \f(1,7)，0<β<π，∴eq \f(π,2)<β<π.
∴－π<α－β<0.而tan(α－β)＝eq \f(1,2)>0，∴－π<α－β<－eq \f(π,2).
∴2α－β＝α＋(α－β)∈(－π，0)．
∵tan(2α－β)＝tan[α＋(α－β)]＝eq \f(tan α＋tanα－β,1－tan αtanα－β)＝1，∴2α－β＝－eq \f(3π,4).
证明恒等式
例5.已知sin(2α＋β)＝3sin β，求证：tan(α＋β)＝2tan α.
【证明】 sin(2α＋β)＝3sin β⇒sin[(α＋β)＋α]＝3sin[(α＋β)－α]
⇒sin(α＋β)cs α＋cs(α＋β)sin α＝3sin(α＋β)cs α－3cs(α＋β)sin α
⇒2sin(α＋β)cs α＝4cs(α＋β)sin α
⇒tan(α＋β)＝2tan α.
所以等式成立。
【类题通法】证明三角恒等式一般采用“由繁到简”、“等价转化”、“往中间凑”等办法，证明时要注意，灵活进行三角变换，有效地沟通条件中的角与问题结论中的角之间的联系，选用恰当的公式快捷求解.
【巩固练习5】证明：eq \f(sin2α＋β,sin α)－2cs(α＋β)＝eq \f(sin β,sin α).
【证明】左边= eq \f(sin2α＋β,sin α)－2cs(α＋β)
＝eq \f(sin2α＋β－2sin αcsα＋β,sin α)
＝eq \f(sin[α＋β＋α]－2sin αcsα＋β,sin α)
＝eq \f(sinα＋βcs α＋csα＋βsin α－2sin αcsα＋β,sin α)
＝eq \f(sinα＋βcs α－csα＋βsin α,sin α)＝eq \f(sin β,sin α)= 右边。
所以等式成立。
（四）操作演练 素养提升
1．已知α是锐角，sin α＝eq \f(3,5)，则cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)＋α))等于( )
A．－eq \f(\r(2),10) B.eq \f(\r(2),10) C．－eq \f(\r(2),5) D.eq \f(\r(2),5)
2.sin 245°sin 125°＋sin 155°sin 35°的值是( )
A．－eq \f(\r(3),2) B．－eq \f(1,2) C.eq \f(1,2) D.eq \f(\r(3),2)
3.已知cs α＝－eq \f(4,5)，且α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))，则tan eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－α))等于( )
A．－eq \f(1,7) B．－7 C.eq \f(1,7) D．7
4..eq \f(1＋tan 12°tan 72°,tan 12°－tan 72°)＝________.
【答案】1.B 2.B 3.D 4.－eq \f(\r(3),3)
【设计意图】通过练习巩固本节所学知识，通过学生解决问题的能力，感悟其中蕴含的数学思想，增强学生的应用意识。
（五）课堂小结，反思感悟
1.知识总结：
2.学生反思：
（1）通过这节课，你学到了什么知识？


（2）在解决问题时，用到了哪些数学思想？


【设计意图】
通过总结，让学生进一步巩固本节所学内容，提高概括能力,提高学生的数学运算能力和逻辑推理能力。
六、布置作业
完成教材：第220页 练习 第1，2，3,4,5题
第229 页 习题3.1 第4,6,9,12,13,14题
课时内容
两角和与差的正弦、余弦和正切公式
简单的三角恒等变换
所在位置
教材第215页
教材第225页
新教材
内容
分析
教材首先利用了圆的旋转对称性推导了两角差的余弦公式，在此基础上，推到了两角和的余弦公式、两角和差的正弦、正切公式以及二倍角公式，是一个逻辑推理的过程，也是认识三角函数式的特征，体会三角恒等变换特点的过程。教材重视对推出公式的理解，应用，重视推导过程所承载的育人功能。
教材通过例题展现三角恒等变换在数学中的应用，引导学生对变换对象和变换目标进行对比、分析，促使学生形成对解题过程中如何选择公式，如何根据条件变形，以及变换过程中体现的换元、逆向使用公式等数学方法的认识，从而进一步理解变换思想，提高学生的推理能力，数学运算素养。
核心素养培养
通过两角和差的公式以及二倍角公式的推导，培养数学抽象的核心素养；通过公式的应用，提升数学运算的核心素养.
通过三角恒等变换，培养数学运算的核心素养。
教学主线
两角差的余弦公式