高中数学人教A版 (2019)选择性必修 第一册2.1 直线的倾斜角与斜率导学案

这是一份高中数学人教A版 (2019)选择性必修 第一册2.1 直线的倾斜角与斜率导学案，共9页。学案主要包含了学习目标，自主学习，小试牛刀，经典例题，跟踪训练，当堂达标，参考答案等内容，欢迎下载使用。

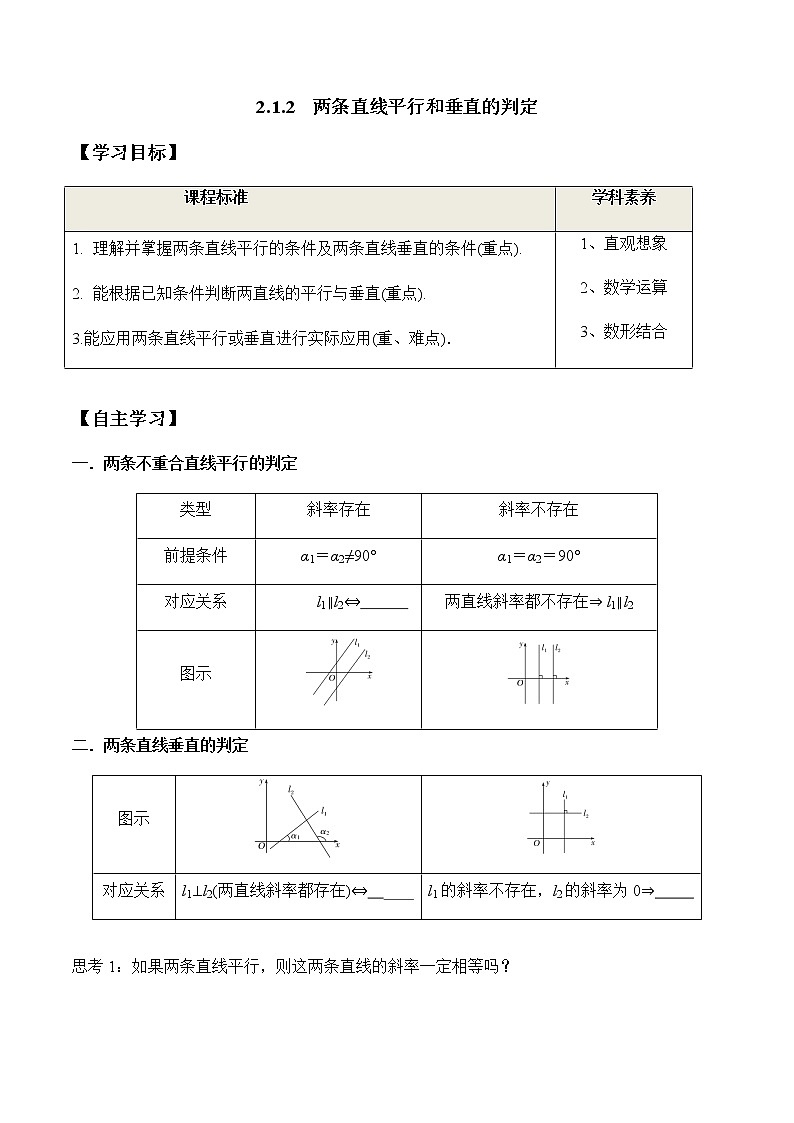
【自主学习】
一．两条不重合直线平行的判定
二．两条直线垂直的判定
思考1：如果两条直线平行，则这两条直线的斜率一定相等吗？
思考2：如果两条直线垂直，则它们的斜率的积一定等于－1吗？
【小试牛刀】
思辨解析(对的打“√”，错的打“×”).
（1）若两条直线的斜率相等，则这两条直线平行.( )
（2）若l1∥l2，则k1＝k2.( )
（3）若两条直线中有一条直线的斜率不存在,另一条直线的斜率存在,则这两条直线垂直.( )
（4）若两条直线的斜率都不存在且两直线不重合，则这两条直线平行.( )
【经典例题】
题型一 两条直线平行的判定
点拨：判断两条不重合的直线是否平行的方法
注意：区分平行与重合，必须强调不共线才能确定平行，因为两直线重合也可以推出两条直线的斜率相等．
例1 下列直线l1与直线l2(l1与l2不重合)平行的有________.(填序号)
①l1经过点A(2,1)，B(－3,5)，l2经过点C(3，－3)，D(8，－7)；
②l1的斜率为2，l2经过点A(1,1)，B(2,2)；
③l1的倾斜角为60°，l2经过点M(1，eq \r(3))，N(－2，－2eq \r(3))；
④l1经过点E(2,6)，F(2,3)，l2经过点P(－3，－3)，Q(－3，－6).
【跟踪训练】1 已知△ABC中，A(0，3)，B(2，－1)，E，F分别为AC，BC的中点，求直线EF的斜率．
题型二 两条直线垂直的判定
点拨：判断两条直线是否垂直的依据是：在这两条直线都有斜率的前提下，只需看它们的斜率之积是否等于－1即可，但应注意有一条直线与x轴垂直，另一条直线与x轴平行或重合时，这两条直线也垂直.
例2 判断下列各题中l1与l2是否垂直.
(1)l1经过点A(－3，－4)，B(1,3)，l2经过点M(－4，－3)，N(3，1)；
(2)l1的斜率为－10，l2经过点A(10,2)，B(20,3)；
(3)l1经过点A(3,4)，B(3,10)，l2经过点M(－10,40)，N(10,40).
【跟踪训练】2已知定点A(－1,3)，B(4,2)，以AB为直径作圆，与x轴有交点C，则交点C的坐标是________．
题型三 平行与垂直的综合应用
点拨：(1)利用直线的斜率判定平面图形的形状一般要运用数形结合的方法，先由图形作出猜测，然后利用直线的斜率关系进行判定.
(2)由几何图形的形状求参数(一般是点的坐标)时，要根据图形的特征确定斜率之间的关系，既要考虑斜率是否存在，又要考虑到图形可能出现的各种情形.
(3)明确运算对象，探究运算思路，是对数学运算的数学核心素养的考查.
例3 已知A(－4，3)，B(2，5)，C(6，3)，D(－3，0)四点，若顺次连接A，B，C，D四点，试判定图形ABCD的形状．
【跟踪训练】3 已知四边形ABCD的顶点B(6，－1)，C(5,2)，D(1,2).若四边形ABCD为直角梯形，求A点坐标.(A，B，C，D按逆时针方向排列)
【当堂达标】
1.过点A(2,5)和点B(－4,5)的直线与直线y＝3的位置关系是( )
A.相交 B.平行 C.重合 D.以上都不对
2.已知两条直线l1,l2的斜率是方程3x2＋mx－3＝0(m∈R)的两个根,则l1与l2的位置关系是( )
A.平行 B.垂直
C.可能重合 D.无法确定
3.(多选)设点P(－4，2)，Q(6，－4)，R(12，6)，S(2，12)，则有( )
A．PQ∥SR B．PQ⊥PS
C．PS∥QS D．PR⊥QS
4.若不同两点P，Q的坐标分别为(a，b)，(3－b,3－a)，则线段PQ的垂直平分线的斜率为________.
5.已知平行四边形ABCD的三个顶点的坐标分别为A(0，1)，B(1，0)，C(4，3)，求顶点D的坐标．
6.已知△ABC的顶点为A(5，－1)，B(1,1)，C(2，m)，若△ABC为直角三角形，求m的值.
【参考答案】
【自主学习】
1.k1＝k2
2.k1·k2＝－1 l1⊥l2
思考1：在两条直线的斜率都存在的情况下，斜率一定相等．
思考2：不一定．它们的斜率也可能一个是0，另一个不存在．
【小试牛刀】
× × × √
【经典例题】
例1 ①③④ 解析 ①∵kAB＝eq \f(5－1,－3－2)＝－eq \f(4,5)，kCD＝eq \f(－7＋3,8－3)＝－eq \f(4,5)，∴kAB＝kCD，∴l1∥l2.
②∵＝eq \f(2－1,2－1)＝1≠＝2，∴l1不平行于l2.
③∵＝tan 60°＝eq \r(3)，＝eq \f(\r(3)＋2\r(3),1＋2)＝eq \r(3)，∴＝，∴l1∥l2.
④l1，l2的斜率均不存在，∴l1∥l2.
【跟踪训练】1 解 ∵E，F分别为AC，BC的中点，
∴EF∥AB，∴kEF＝kAB＝eq \f(－1－3,2－0)＝－2.故直线EF的斜率为－2.
例2 解 (1)k1＝eq \f(3－－4,1－－3)＝eq \f(7,4)，k2＝eq \f(1－－3,3－－4)＝eq \f(4,7)，k1k2＝1，∴l1与l2不垂直.
(2)k1＝－10，k2＝eq \f(3－2,20－10)＝eq \f(1,10)，k1k2＝－1，∴l1⊥l2.
(3)l1的倾斜角为90°，则l1⊥x轴；k2＝eq \f(40－40,10－－10)＝0，则l2∥x轴，∴l1⊥l2.
【跟踪训练】2 (1,0)或(2,0) 解析 设以A、B为直径的圆与x轴的交点为P(x,0)，
∵kPB≠0，kPA≠0，∴kPA·kPB＝－1，即eq \f(0－3,x＋1)·eq \f(0－2,x－4)＝－1，
∴(x＋1)(x－4)＝－6，而x2－3x＋2＝0.∴x＝1或x＝2，∴P点坐标为(1,0)或(2,0)．
例3 解 A，B，C，D四点在坐标平面内的位置如图：
由斜率公式可得
kAB＝eq \f(5－3,2－（－4）)＝eq \f(1,3)，kCD＝eq \f(0－3,－3－6)＝eq \f(1,3)，kAD＝eq \f(0－3,－3－（－4）)＝－3，kBC＝eq \f(3－5,6－2)＝－eq \f(1,2)，
∴kAB＝kCD，由图可知AB与CD不重合，∴AB∥CD.
由kAD≠kBC，∴AD与BC不平行．又kAB·kAD＝eq \f(1,3)×(－3)＝－1，∴AB⊥AD.
故四边形ABCD为直角梯形．
【跟踪训练】3 解 ①若∠A＝∠D＝90°，如图(1)，
由已知AB∥DC，AD⊥AB，而kCD＝0，故A(1，－1).
②若∠A＝∠B＝90°，如图(2).
设A(a，b)，则kBC＝－3，kAD＝eq \f(b－2,a－1)，kAB＝eq \f(b＋1,a－6).
由AD∥BC，得kAD＝kBC，即eq \f(b－2,a－1)＝－3；①
由AB⊥BC，得kAB·kBC＝－1，即eq \f(b＋1,a－6)·(－3)＝－1.②
由①②得eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝\f(12,5)，,b＝－\f(11,5)，))故Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(12,5)，－\f(11,5))).
综上所述，A点坐标为(1，－1)或eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(12,5)，－\f(11,5))).
【当堂达标】
1. B 解析：斜率都为0且不重合，所以平行.
2.B 解析：由方程3x2＋mx－3＝0，知Δ＝m2－4×3×(－3)＝m2＋36>0恒成立.
故方程有两相异实根，即l1与l2的斜率k1，k2均存在.设两根为x1，x2，则k1k2＝x1x2＝－1，所以l1⊥l2.
3.ABD 解析：由斜率公式知，kPQ＝ eq \f(－4－2,6＋4) ＝－ eq \f(3,5) ，kSR＝ eq \f(12－6,2－12) ＝－ eq \f(3,5) ，
kPS＝ eq \f(12－2,2＋4) ＝ eq \f(5,3) ，kQS＝ eq \f(12＋4,2－6) ＝－4，kPR＝ eq \f(6－2,12＋4) ＝ eq \f(1,4) ，所以PQ∥SR，PQ⊥PS，PR⊥QS.而kPS≠kQS，所以PS与QS不平行．
4.－1 解析 由kPQ＝eq \f(3－a－b,3－b－a)＝1，得线段PQ的垂直平分线的斜率为－1.
5．解 设D(m，n)，由题意，得AB∥DC，AD∥BC，则有kAB＝kDC，kAD＝kBC.
∴eq \b\lc\{(\a\vs4\al\c1(\f(0－1,1－0)＝\f(3－n,4－m)，,\f(n－1,m－0)＝\f(3－0,4－1)，))解得eq \b\lc\{(\a\vs4\al\c1(m＝3，,n＝4.))∴顶点D的坐标为(3，4)．
6.解 若∠A为直角，则AC⊥AB，∴kAC·kAB＝－1，即eq \f(m＋1,2－5)·eq \f(1＋1,1－5)＝－1，解得m＝－7；
若∠B为直角，则AB⊥BC，∴kAB·kBC＝－1，即eq \f(1＋1,1－5)·eq \f(m－1,2－1)＝－1，解得m＝3；
若∠C为直角，则AC⊥BC，∴kAC·kBC＝－1，即eq \f(m＋1,2－5)·eq \f(m－1,2－1)＝－1，解得m＝±2.
综上所述，m＝－7或m＝3或m＝±2.课程标准
学科素养
理解并掌握两条直线平行的条件及两条直线垂直的条件(重点).
能根据已知条件判断两直线的平行与垂直(重点).
3.能应用两条直线平行或垂直进行实际应用(重、难点)．
1、直观想象
2、数学运算
3、数形结合
类型
斜率存在
斜率不存在
前提条件
α1＝α2≠90°
α1＝α2＝90°
对应关系
l1∥l2⇔
两直线斜率都不存在⇒ l1∥l2
图示
图示
对应关系
l1⊥l2(两直线斜率都存在)⇔
l1的斜率不存在，l2的斜率为0⇒