选择性必修 第一册第二章 直线和圆的方程2.2 直线的方程学案

这是一份选择性必修 第一册第二章 直线和圆的方程2.2 直线的方程学案，共7页。学案主要包含了学习目标，自主学习，小试牛刀，经典例题，跟踪训练，当堂达标，参考答案等内容，欢迎下载使用。

【自主学习】
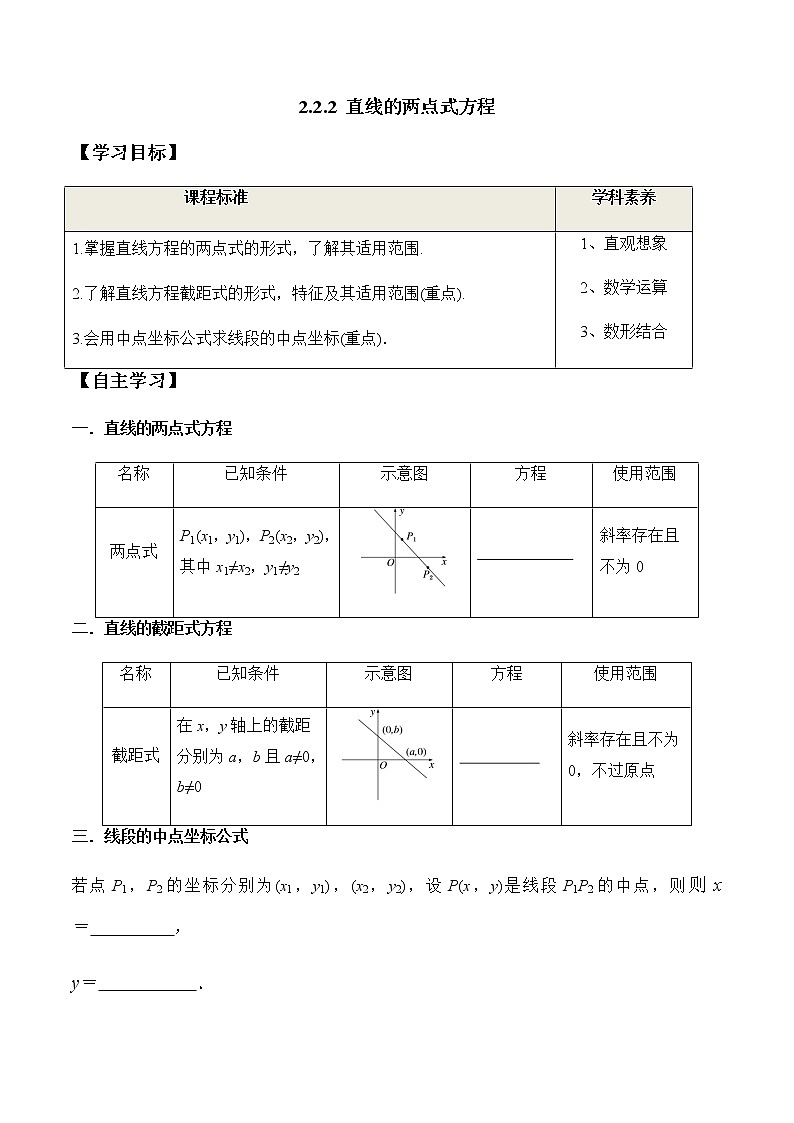
一．直线的两点式方程
二．直线的截距式方程
三．线段的中点坐标公式
若点P1，P2的坐标分别为(x1，y1)，(x2，y2)，设P(x，y)是线段P1P2的中点，则则x＝ ，
y＝ ．
思考1： 过点(1，3)和(1，5)的直线能用两点式表示吗？为什么？过点(2，3)，(5，3)的直线呢？
思考2： 截距式方程能否表示过原点的直线？
【小试牛刀】
思考辨析(正确的打“√”，错误的打“×”)
（1）不经过原点的直线都可以用方程eq \f(x,a)＋eq \f(y,b)＝1表示.( )
（2）能用两点式方程表示的直线也可用点斜式方程表示.( )
（3）能用截距式方程表示的直线都能用两点式表示.( )
（4）直线y＝x在x轴和y轴上的截距均为0.( )
【经典例题】
题型一 直线的两点式方程
点拨：当已知两点坐标，求过这两点的直线方程时，首先要判断是否满足两点式方程的适用条件：两点的连线不平行于坐标轴.若满足，则考虑用两点式求方程.
例1 如图，已知A(1,2)，B(－1,4)，C(5,2).
①求线段AB中点D的坐标；
②求△ABC的边AB上的中线所在的直线方程.
【跟踪训练】1 (1)过(1，1)，(2，－1)两点的直线方程为( )
A．2x－y－1＝0 B．x－2y＋3＝0
C．2x＋y－3＝0 D．x＋2y－3＝0
经过M(3,2)与N(6,2)两点的直线方程为( )
A.x＝2 B.y＝2 C.x＝3 D.x＝6
题型二 直线的截距式方程
点拨： (1)如果问题中涉及直线与两坐标轴相交，则可考虑选用直线截距式的方程，用待定系数法确定其系数即可.
(2)选用直线截距式的方程时，必须首先考虑直线能否过原点以及能否与两坐标轴垂直.
零截距：如果题目中出现直线在两坐标轴上的“截距相等”、“截距互为相反数”、“在一坐标轴上的截距是另一坐标轴上截距的m倍(m>0)”等条件时，采用截距式求直线方程，一定要注意考虑“零截距”的情况．
例2 求过点A(3，4)，且在两坐标轴上的截距截距相等的直线l的方程。
【跟踪训练】2 (1)求过点A(4，2)，且在两坐标轴上的截距的绝对值相等的直线l的方程．
(2)已知直线l过点A(1,2)，且与两坐标轴的正半轴围成的三角形的面积是4，求直线l的方程.
【当堂达标】
1.(多选)下列说法正确的是( )
A.不经过原点的直线都可以表示为eq \f(x,a)＋eq \f(y,b)＝1
B.若直线与两轴交点分别为A、B且AB的中点为(4,1)则直线l的方程为eq \f(x,8)＋eq \f(y,2)＝1
C.过点(1,1)且在两轴上截距相等的直线方程为y＝x或x＋y＝2
D.直线3x－2y＝4的截距式方程为eq \f(x,\f(4,3))＋eq \f(y,－2)＝1
2.过两点(－2，1)和(1，4)的直线方程为( )
A．y＝x＋3 B．y＝－x＋1 C．y＝x＋2 D．y＝－x－2
3.过点P(4，－3)且在坐标轴上截距相等的直线有( )
A．1条 B．2条 C．3条 D．4条
4.已知点A(3,2)，B(－1,4)，则经过点C(2,5)且经过线段AB的中点的直线方程为________.
5.过点P(1,2)且在两坐标轴上截距的和为0的直线方程为____________________.
6.直线l经过点A(－3，4)，且在x轴上的截距是在y轴上的截距的2倍，求该直线的方程．
【参考答案】
【自主学习】
eq \f(y－y1,y2－y1)＝eq \f(x－x1,x2－x1) eq \f(x,a)＋eq \f(y,b)＝1
思考1：不能，因为1－1＝0，而0不能做分母．过点(2，3)，(5，3)的直线也不能用两点式表示．
思考2：不能，因为ab≠0，即有两个非零截距．
【小试牛刀】
× √ √ √
【经典例题】
例1 解 ①因为A(1,2)，B(－1,4)，所以线段AB中点D的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1＋－1,2)，\f(2＋4,2)))，即D(0,3).
②△ABC的边AB上的中线即线段CD，因为C(5,2)，D(0,3).所以线段CD所在的直线方程为eq \f(y－3,2－3)＝eq \f(x－0,5－0)，化简可得x＋5y－15＝0.
【跟踪训练】1 (1) C 解析 ∵直线过两点(1，1)和(2，－1)，∴直线的两点式方程为eq \f(y－（－1）,1－（－1）)＝eq \f(x－2,1－2)，整理得2x＋y－3＝0，故选C.
(2)B 解析 由M，N两点的坐标可知，直线MN与x轴平行，所以直线方程为y＝2，故选B.
例2 解 (1)当截距不为0时，设直线l的方程为eq \f(x,a)＋eq \f(y,a)＝1，又知l过(3，4)，
∴eq \f(3,a)＋eq \f(4,a)＝1，解得a＝7，∴直线l的方程为x＋y－7＝0.
(2)当截距为0时，直线方程为y＝eq \f(4,3)x，即4x－3y＝0.
综上，直线l的方程为x＋y－7＝0或4x－3y＝0.
【跟踪训练】2（1）解 当直线过原点时，它在x轴、y轴上的截距都是0，满足题意．
此时，直线的斜率为eq \f(1,2)，所以直线l的方程为y＝eq \f(1,2)x，即x－2y＝0.
当直线不过原点时，由题意可设直线方程为eq \f(x,a)＋eq \f(y,b)＝1.
又因为过点A，所以eq \f(4,a)＋eq \f(2,b)＝1. ①
因为直线在两坐标轴上的截距的绝对值相等，所以|a|＝|b|. ②
由①②联立方程组，
解得eq \b\lc\{(\a\vs4\al\c1(a＝6，,b＝6))或eq \b\lc\{(\a\vs4\al\c1(a＝2，,b＝－2.))所以所求直线的方程为eq \f(x,6)＋eq \f(y,6)＝1或eq \f(x,2)＋eq \f(y,－2)＝1，
化简得直线l的方程为x＋y＝6或x－y＝2，即直线l的方程为x＋y－6＝0或x－y－2＝0，
综上，直线l的方程为x－2y＝0或x＋y－6＝0或x－y－2＝0.
（2）解 设l：eq \f(x,a)＋eq \f(y,b)＝1(a>0，b>0)，则eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(1,2)ab＝4，,\f(1,a)＋\f(2,b)＝1.))a2－4a＋4＝0，解得a＝2，所以b＝4.
直线l：eq \f(x,2)＋eq \f(y,4)＝1，所以l：2x＋y－4＝0.
【当堂达标】
1.BCD解析：A中，与坐标轴垂直的直线也不能用截距式表示，故A错；B中，AB的中点为(4,1)，那么A(8,0)，B(0,2)的直线方程为eq \f(x,8)＋eq \f(y,2)＝1，故B对；C中过原点时，直线为y＝x，不过原点时直线为x＋y＝2，故C对；D中，方程3x－2y＝4可化为eq \f(x,\f(4,3))＋eq \f(y,－2)＝1，故D对．
2. A 解析：代入两点式得直线方程eq \f(y－1,4－1)＝eq \f(x＋2,1＋2)，整理得y＝x＋3.
B 解析：当直线过原点时显然符合条件；当直线不过原点时，设所求直线的方程为eq \f(x,a)＋eq \f(y,a)＝1，把点P(4，－3)代入方程得a＝1.因而所求直线有2条．
4.2x－y＋1＝0 解析：AB的中点坐标为(1,3)，由直线的两点式方程可得eq \f(y－3,5－3)＝eq \f(x－1,2－1)，
即2x－y＋1＝0.
5.2x－y＝0或x－y＋1＝0 解析：当直线过原点时，得直线方程为2x－y＝0；
当在坐标轴上的截距不为零时，可设直线方程为eq \f(x,a)－eq \f(y,a)＝1，
将x＝1，y＝2代入方程可得a＝－1，得直线方程为x－y＋1＝0.
∴直线方程为2x－y＝0或x－y＋1＝0.
6.解：当直线经过原点时，直线方程为：y＝－eq \f(4,3)x.
当直线不经过原点时，设直线方程为：eq \f(x,2a)＋eq \f(y,a)＝1，
把点A(－3，4)代入，得eq \f(－3,2a)＋eq \f(4,a)＝1，解得a＝eq \f(5,2).
∴直线方程为x＋2y＝5.
综上可得直线方程为：4x＋3y＝0或x＋2y－5＝0.课程标准
学科素养
1.掌握直线方程的两点式的形式，了解其适用范围.
2.了解直线方程截距式的形式，特征及其适用范围(重点).
3.会用中点坐标公式求线段的中点坐标(重点)．
1、直观想象
2、数学运算
3、数形结合
名称
已知条件
示意图
方程
使用范围
两点式
P1(x1，y1)，P2(x2，y2)，其中x1≠x2，y1≠y2

斜率存在且不为0
名称
已知条件
示意图
方程
使用范围
截距式
在x，y轴上的截距分别为a，b且a≠0，b≠0

斜率存在且不为0，不过原点