统考版高考物理一轮复习第一章运动的描述匀变速直线运动的研究第2讲匀变速直线运动的规律含答案（试卷）

这是一份统考版高考物理一轮复习第一章运动的描述匀变速直线运动的研究第2讲匀变速直线运动的规律含答案（试卷），共20页。试卷主要包含了匀变速直线运动的规律，自由落体运动和竖直上抛运动等内容，欢迎下载使用。
必备知识·自主排查
一、匀变速直线运动的规律
1．定义和分类
(1)定义：沿着一条直线，且________不变的运动叫做匀变速直线运动．
(2)分类：匀加速直线运动：a、v方向________．匀减速直线运动：a、v方向________．
2．基本规律
(1)速度公式：v＝________．
(2)位移公式：x＝________．
(3)速度位移关系式：v2−v02＝______．
3．三个重要推论
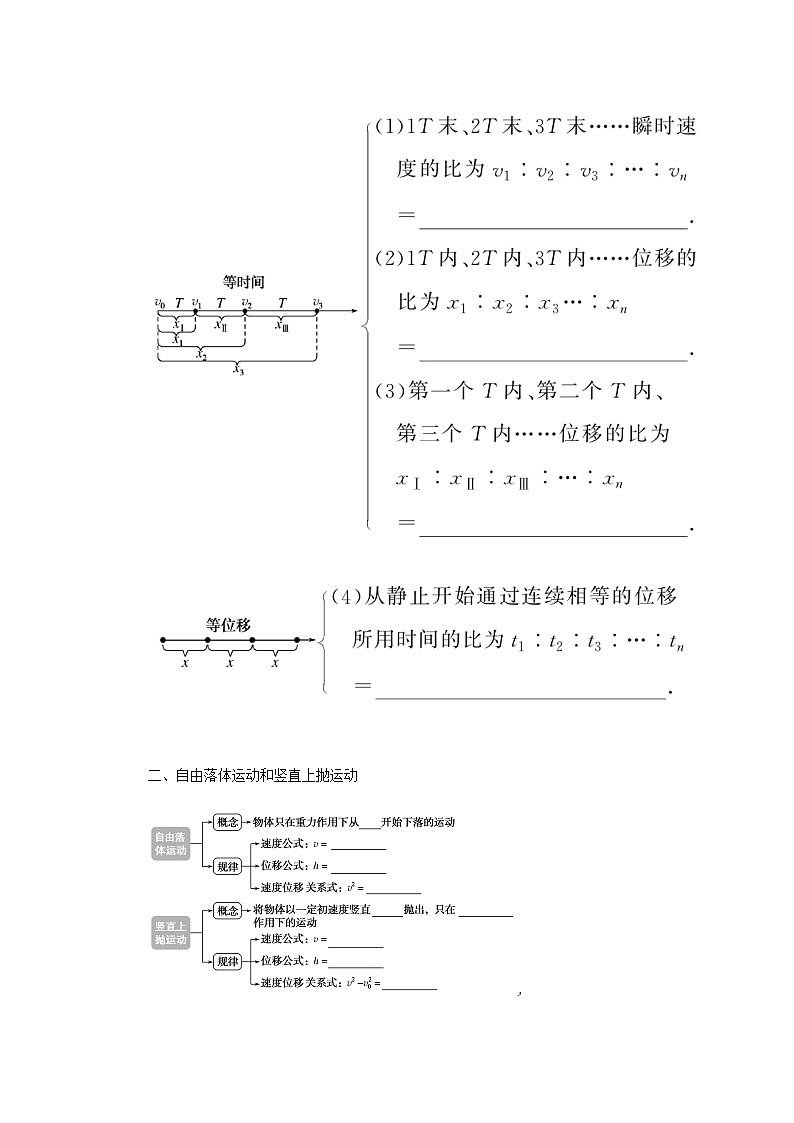
4．初速度为零的匀变速直线运动的四个推论
二、自由落体运动和竖直上抛运动
,
生活情境
1.一辆汽车从静止出发，在交通灯变绿时从A点以2.0 m/s2的加速度在平直的公路上做匀加速直线运动，经一段时间运动到B点，速度达20 m/s，则
(1)汽车在运动过程中，速度是均匀增加的．( )
(2)汽车在运动过程中，位移是均匀增加的．( )
(3)汽车在运动过程中，在任意相等的时间内，速度的变化量是相等的．( )
(4)汽车从A点运动到B点所用时间为10 s，位移为100 m．( )
(5)汽车从A点运动到B点，中间时刻的速度为10 m/s.( )
(6)汽车从A点运动到B点，位移中点的速度为102 m/s.( )
教材拓展
2.[鲁科版必修1P36T1改编]关于匀变速直线运动，下列说法正确的是( )
A．在相等时间内位移的变化相同
B．在相等时间内速度的变化相同
C．在相等时间内加速度的变化相同
D．在相等路程内速度的变化相同
3．[人教版必修1P43T3改编]某航母跑道长160 m，飞机发动机产生的最大加速度为5 m/s2，起飞需要的最低速度为50 m/s，飞机在航母跑道上起飞的过程可以简化为做匀加速直线运动，若航母沿飞机起飞方向以某一速度匀速航行，为使飞机安全起飞，航母匀速运动的最小速度为( )
A．10 m/s B．15 m/s
C．20 m/s D．30 m/s
关键能力·分层突破
考点一 匀变速直线运动规律的应用
1．运动学公式中符号的规定
一般规定初速度的方向为正方向，与初速度同向的物理量取正值，反向的物理量取负值．若v0＝0，一般以a的方向为正方向．
2．匀变速直线运动公式的选用
一般问题用两个基本公式可以解决，以下特殊情况下用导出公式会提高解题的速度和准确率；
(1)不涉及时间，选择v2−v02＝2ax；
(2)不涉及加速度，用平均速度公式，比如纸带问题中运用vt2＝v＝xt求瞬时速度；
(3)处理纸带问题时用Δx＝x2－x1＝aT2，xm－xn＝(m－n)aT2求加速度．
角度1基本公式的应用
例1 ETC是电子不停车收费系统的简称，汽车分别通过ETC通道和人工收费通道的流程如图所示．假设汽车以v1＝12 m/s的速度朝收费站沿直线行驶，如果过ETC通道，需要在距收费站中心线前d＝10 m处正好匀减速至v2＝4 m/s，匀速通过中心线后，再匀加速至v1正常行驶；如果过人工收费通道，需要恰好在中心线处匀减速至零，经过t0＝20 s缴费成功后，再启动汽车匀加速至v1正常行驶，设汽车加速和减速过程中的加速度大小均为1 m/s2.求：
(1)汽车过ETC通道时，从开始减速到恢复正常行驶过程中的位移大小；
(2)汽车过人工收费通道时，应在离收费站中心线多远处开始减速；
(3)汽车过ETC通道比过人工收费通道节约的时间．
教你解决问题
(1)读题审题——获取信息
(2)思维转化——模型建构
①过ETC通道时经历三个运动阶段：
②过人工收费通道经历两个运动阶段：
角度2 推论的应用
例2.如图所示，哈大高铁运营里程为921 km，设计时速为350 km.某列车到达大连北站时刹车做匀减速直线运动，开始刹车后第5 s内的位移是57.5 m，第10 s内的位移是32.5 m，已知10 s末列车还未停止运动，则下列说法正确的是( )
A．在研究列车从哈尔滨到大连所用时间时不能把列车看成质点
B．921 km是指位移
C．列车做匀减速直线运动时的加速度大小为6.25 m/s2
D．列车在开始刹车时的速度为80 m/s
[思维方法]
解决运动学问题的基本思路：
跟进训练
1.(多选)一名消防队员在模拟演习训练中，沿着长为12 m的竖立在地面上的钢管从顶端由静止先匀加速再匀减速下滑，滑到地面时速度恰好为零．如果他加速时的加速度大小是减速时加速度大小的2倍，下滑的总时间为3 s，那么该消防队员( )
A．下滑过程中的最大速度为4 m/s
B．加速与减速运动过程的时间之比为1∶2
C．加速与减速运动过程中平均速度之比为1∶1
D．加速与减速运动过程的位移大小之比为1∶4
2．[2022·河南模拟]如图所示，物体自O点由静止开始做匀加速直线运动，A、B、C、D为其运动轨迹上的四点，测得AB＝2 m，BC＝4 m，且物体通过AB、BC、CD所用的时间均为t＝1 s，求物体的加速度大小a和OD之间的距离．
考点二 自由落体运动和竖直上抛运动
角度1自由落体运动(一题多变)
例3.如图所示，屋檐上水滴下落的过程可以近似地看作是自由落体运动．假设水滴从10 m高的屋檐上无初速度滴落，水滴下落到地面时的速度大约是多大？(g取10 m/s2)
【考法拓展】在[例3]中水滴下落过程中经过2 m高的窗户所需时间为0.2 s．那么窗户上沿到屋檐的距离为多少？
角度2竖直上抛运动(一题多解)
例4. 气球以10 m/s的速度匀速上升，当它上升到离地175 m的高处时，一重物从气球上脱落，则重物需要经过多长时间才能落到地面？到达地面时的速度是多大？(g取10 m/s2)
[思维方法]
竖直上抛运动的研究方法
(1)分段研究法：
(2)整体研究法：
取初速度的方向为正方向，全过程为初速度为v0，加速度大小为g的匀变速直线运动．
其规律符合h＝v0t－12gt2 v＝v0−gt，v2−v02＝－2gh.
拓展点 刹车类问题和双向可逆类问题
1.刹车类问题中的两点提醒
(1)分清运动时间与刹车时间之间的大小关系．
(2)确定能否使用逆向思维法，所研究阶段的末速度为零，一般都可应用逆向思维法．
2．双向可逆运动的特点
这类运动的速度减到零后，以相同加速度反向加速．如竖直上抛、沿光滑斜面向上滑动．
例5. (多选)一物体以5 m/s的初速度在光滑斜面上向上做匀减速运动，其加速度大小为2ms2，设斜面足够长，经过t时间物体位移的大小为4 m，则时间t可能为( )
A．1 s B．3 s C．4 s D．5+412 s
跟进训练
3.如图所示，在离地面一定高度处把4个水果以不同的初速度竖直上抛，不计空气阻力，若1 s后4个水果均未着地，则1 s后速率最大的是(g取10 m/s2)( )
4．有一辆汽车在能见度较低的雾霾天气里以54 km/h的速度匀速行驶，司机突然看到正前方有一辆静止的故障车，该司机刹车的反应时间为0.6 s，刹车后汽车匀减速前进．刹车过程中加速度大小为5 m/s2，最后停在故障车后1.5 m处，避免了一场事故，以下说法正确的是( )
A．司机发现故障车后，汽车经过3 s停下
B．司机发现故障车时，汽车与故障车的距离为33 m
C．从司机发现故障车到停下来的过程，汽车的平均速度为7.5 m/s
D．从司机发现故障车到停下来的过程，汽车的平均速度为10.5 m/s
考点三 匀变速直线运动中的STSE问题素养提升
匀变速运动与交通、体育和生活等紧密联系，常见的匀变速直线运动STSE问题有行车安全、交通通行和体育运动等，解决这类问题的关键：
(1)建模——建立运动的模型(列出运动方程)；
(2)分段——按照时间顺序，分阶段研究运动．
情境1 “智能物流机器人”
(多选)
为解决疫情下“最后500米”配送的矛盾，将“人传人”的风险降到最低，目前一些公司推出了智能物流机器人．机器人运动的最大速度为1 m/s，当它过红绿灯路口时，发现绿灯时间是20 s，路宽是19.5 m，它启动的最大加速度是0.5ms2，下面是它过马路的安排方案，既能不闯红灯，又能安全通过的方案是( )
A．在停车线等绿灯亮起，以最大加速度启动
B．在距离停车线1 m处，绿灯亮起之前2 s，以最大加速度启动
C．在距离停车线2 m处，绿灯亮起之前2 s，以最大加速度启动
D．在距离停车线0.5 m处，绿灯亮起之前1 s，以最大加速度启动
情境2 酒驾
(多选)酒后驾驶会导致许多安全隐患，这是因为驾驶员的反应时间变长．反应时间是指驾驶员从发现情况到采取制动的时间．下表中“思考距离”是指驾驶员发现情况到采取制动的时间内汽车的行驶距离，“制动距离”是指驾驶员发现情况到汽车停止行驶的距离．(假设汽车制动加速度都相同)
分析上表可知，下列说法正确的是( )
A．驾驶员正常情况下反应时间为0.5 s
B．驾驶员酒后反应时间比正常情况慢0.5 s
C．驾驶员采取制动措施后汽车加速度大小为3.75 m/s2
D．当车速为25 m/s时，发现前方60 m处有险情，酒驾者不能安全停车
拓展点 有关汽车行驶的几个概念
1.反应时间：人从发现情况到采取相应的行动经过的时间叫反应时间．
2．反应距离：驾驶员发现前方有危险时，必须先经过一段反应时间后才能做出制动动作，在反应时间内汽车以原来的速度行驶，所行驶的距离称为反应距离．
3．刹车距离：从制动刹车开始到汽车完全停下来，汽车做匀减速直线运动，所通过的距离叫刹车距离．
4．停车距离：反应距离和刹车距离之和就是停车距离．
5．安全距离：指在同车道行驶的机动车，后车与前车保持的最短距离，安全距离包含反应距离和刹车距离两部分．
情境3 机动车礼让行人
[2021·浙江6月，19]机动车礼让行人是一种文明行为．如图所示，质量m＝1.0×103 kg的汽车以v1＝36 km/h的速度在水平路面上匀速行驶，在距离斑马线s＝20 m处，驾驶员发现小朋友排着长l＝6 m的队伍从斑马线一端开始通过，立即刹车，最终恰好停在斑马线前．假设汽车在刹车过程中所受阻力不变，且忽略驾驶员反应时间．
(1)求开始刹车到汽车停止所用的时间和所受阻力的大小；
(2)若路面宽L＝6 m，小朋友行走的速度v0＝0.5 m/s，求汽车在斑马线前等待小朋友全部通过所需的时间；
(3)假设驾驶员以v2＝54 km/h超速行驶，在距离斑马线s＝20 m处立即刹车，求汽车到斑马线时的速度．
[思维方法]
解决STSE问题的方法
在解决生活和生产中的实际问题时．
(1)根据所描述的情景 分析 物理过程 建构 物理模型．
(2)分析各阶段的物理量．
(3)选取合适的匀变速直线运动规律求解．
第2讲 匀变速直线运动的规律
必备知识·自主排查
一、
1．（1）加速度 （2）相同 相反
2．（1）v0＋at （2）v0t＋12at2 （3）2ax
4．（1）1∶2∶3∶…∶n
（2）12∶22∶32∶…∶n2
（3）1∶3∶5∶…∶（2n－1）
（4）1∶（2－1）∶（3－2）∶…∶（n－n−1）
二、
静止 gt 12gt2 2gh 向上 重力 v0－gt v0t－12gt2 －2gh
生活情境
1．（1）√ （2）× （3）√ （4）√ （5）√ （6）√
教材拓展
2．答案：B
3．答案：A
关键能力·分层突破
例1 解析：（1）过ETC通道时，减速的位移和加速的位移相等，则
x1＝ eq \f(v eq \\al(\s\up1(2),\s\d1(1)) －v eq \\al(\s\up1(2),\s\d1(2)) ,2a) ＝64 m
故总的位移x总1＝2x1＋d＝138 m
（2）过人工收费通道时，开始减速时距离中心线为
x2＝ eq \f(v eq \\al(\s\up1(2),\s\d1(1)) ,2a) ＝72 m
（3）过ETC通道的时间
t1＝ eq \f(v1－v2,a) ×2＋ eq \f(d,v2) ＝18.5 s
过人工收费通道的时间
t2＝ eq \f(v1,a) ×2＋t0＝44 s
x总2＝2x2＝144 m
二者的位移差Δx＝x总2－x总1＝6 m
在这段位移内汽车以正常行驶速度做匀速直线运动，则Δt＝t2－ eq \b\lc\(\rc\)(\a\vs4\al\c1(t1＋\f(Δx,v1))) ＝25 s
答案：（1）138 m （2）72 m （3）25 s
例2 解析：因列车的长度远小于哈尔滨到大连的距离，故研究列车行驶该路程所用时间时可以把列车视为质点，选项A错误；由位移与路程的意义知921 km是指路程，选项B错误；由xn－xm＝（n－m）aT2，解得加速度a＝ eq \f(32.5 m－57.5 m,5×（1 s）2) ＝－5 m/s2，即加速度大小为5 m/s2，选项C错误；匀变速直线运动中平均速度等于中间时刻的瞬时速度，则第4.5 s末列车速度为57.5 m/s，由速度公式可得v0＝v－at＝57.5 m/s－（－5 m/s2×4.5 s）＝80 m/s，选项D正确．
答案：D
1．解析：钢管长L＝12 m，运动总时间t＝3 s，加速过程加速度大小2a、时间t1、位移x1、最大速度v，减速过程加速度大小a、时间t2、位移x2.加速和减速过程中平均速度均为v2， vt2＝L，得v＝8 m/s，A项错误，C项正确；v＝2at1＝at2，t1∶t2＝1∶2，B项正确；x1＝vt12，x2＝vt22，x1∶x2＝1∶2，D项错误．
答案：BC
2．解析：由匀变速直线运动的推论Δx＝aT2
可得a＝ΔxT2＝Δxt2＝2 m/s2
由于CD－BC＝BC－AB
代入数据有CD＝6 m
由中间时刻的瞬时速度等于这段时间内的平均速度，可以得到B点的速度vB＝2＋42×1 m/s＝3 m/s
由2ax＝v2－v02
得OB＝vB2−02×a＝322×1 m＝2.25 m
故OD＝OB＋BC＋CD＝（2.25＋4＋6） m＝12.25 m
故物体的加速度大小a和OD之间的距离分别为2 m/s2，12.25 m.
答案：2 m/s2 12.25 m
例3 解析：选取水滴最初下落点为位移的起点，竖直向下为正方向，由自由落体运动规律知x＝12gt2，v＝gt
联立得v＝2gx
代入数据得v＝2×10×10m/s≈14 m/s
即水滴下落到地面的瞬间，速度大约是14 m/s.
答案：14 m/s
[考法拓展] 解析：设水滴下落到窗户上沿时的速度为v0，则由x＝v0t＋12gt2得，2＝v0×0.2＋12×10×0.22
解得v0＝9 m/s
根据v02＝2gx，得
窗户上沿到屋檐的距离x＝v022g＝922×10 m＝4.05 m.
答案：4.05 m
例4 解析：方法一 把竖直上抛运动过程分段研究
设重物离开气球后，经过t1时间上升到最高点，
则t1＝v0g＝1010 s＝1 s.
上升的最大高度
h1＝ eq \f(v eq \\al(\s\up1(2),\s\d1(0)) ,2g) ＝ eq \f(102,2×10) m＝5 m. 12
故重物离地面的最大高度为
H＝h1＋h＝5 m＋175 m＝180 m.
重物从最高处自由下落，落地时间和落地速度分别为
t2＝ eq \r(\f(2H,g)) ＝ eq \r(\f(2×180,10)) s＝6 s.
v＝gt2＝10×6 m/s＝60 m/s.
所以重物从气球上脱落至落地共历时
t＝t1＋t2＝7 s.
方法二 取全过程作一整体进行研究
从物体自气球上脱落计时，经时间t落地，规定初速度方向为正方向，画出运动草图如图所示，则物体在时间t内的位移
h＝－175 m.
由位移公式
h＝v0t－12gt2有，
－175＝10t－12×10t2，
解得t＝7 s和t＝－5 s（舍去），
所以重物落地速度为
v1＝v0－gt＝10 m/s－10×7 m/s＝－60 m/s.
其中负号表示方向向下，与初速度方向相反．
方法三 对称法
根据速度对称知，重物返回脱离点时，具有向下的速度v0＝10 m/s，设落地速度为v，则v2－v eq \\al(\s\up11(2),\s\d4(0)) ＝2gh.
解得v＝60 m/s，方向竖直向下．
经过h历时Δt＝ eq \f(v－v0,g) ＝5 s.
从最高点到落地历时t1＝ eq \f(v,g) ＝6 s.
由时间对称可知，重物脱落后至落地历时t＝2t1－Δt＝7 s.
答案：7 s 60 m/s
例5 解析：以沿斜面向上为正方向，当物体的位移为4 m时，
根据x＝v0t＋12at2得
4＝5t－12×2t2
解得t1＝1 s，t2＝4 s
当物体的位移为－4 m时，
根据x＝v0t＋12at2得
－4＝5t－12×2t2
解得t3＝5＋412s，故A、C、D正确，B错误．
答案：ACD
3．解析：根据v＝v0＋at，v0A＝－3 m/s.代入解得vA＝7 m/s，同理解得vB＝5 m/s，vC＝0 m/s，vD＝－5 m/s.由于|vA|>|vB|＝|vD|>|vC|，故A正确，B、C、D错误．
答案：A
4．解析：v0＝54 km/h＝15 m/s，汽车刹车时间t2v0a＝3 s，故汽车运动总时间t＝t1＋t2＝0.6 s＋3 s＝3.6 s，故A项错误；司机发现故障车时，汽车与故障车的距离为x＝v0t1＋ eq \f(v0,2) t2＋1.5 m＝15×0.6 m＋ eq \f(15,2) ×3 m＋1.5 m＝33 m，故B项正确；汽车的平均速度 eq \(v,\s\up6(－)) ＝ eq \f(v0t1＋\f(v0,2)t2,t1＋t2) ＝ eq \f(9＋22.5,3.6) m/s＝8.75 m/s，故C、D两项错误，故选B项．
答案：B
情境1 解析：机器人在停车线等绿灯亮起后，需要t1＝va＝10.5s＝2 s达到最大速度，位移是x1＝12at12＝1 m，匀速运动的位移x2＝l－x1＝18.5 m，需要时间为t2＝x2v＝18.5 s，两次运动时间之和为20.5 s，不安全，故A不对；在距离停车线1 m处以最大加速度启动2 s，正好绿灯亮，机器人也正好到了停车线，再经过19.5 s，过了马路，这个方案是可以的，故B对；在距离停车线2 m处，机器人启动2 s后，走了1 m，距离停车线还有1 m，这时绿灯亮起，机器人距离马路另外一端还有20.5 m，需要20.5 s通过，而绿灯时间为20 s，所以不安全，故C不对；在距离停车线0.5 m处，1 s后绿灯亮起，其位移为x＝12at2＝0.25 m，小于0.5 m，故没有闯红灯，继续前进0.75 m，达到最大速度，共用去了2 s，绿灯还有19 s，这时剩下的距离还有19 m，正好通过马路，故D对．
答案：BD
情境2 解析：反应时间＝思考距离÷车速，因此正常情况下反应时间为0.5 s，酒后反应时间为1 s，故A、B正确；设汽车从开始制动到停车的位移为x，则x＝x制动－x思考，根据匀变速直线运动公式v2＝2ax，解得a＝7.5 m/s2，C错误；根据表格知，车速为25 m/s时，酒后制动距离为66.7 m>60 m，故不能安全停车，D正确．
答案：ABD
情境3 解析：（1）设汽车刹车过程的加速度大小为a，所用时间为t1，所受阻力大小为Ff
由运动学公式得v12＝2as①
v1＝at1②
由牛顿第二定律得Ff＝ma③
联立①②③解得t1＝4 s④
Ff＝2.5×103 N⑤
（2）设汽车等待时间为t，小朋友匀速过马路所用时间为t2
则由运动学公式得l＋L＝v0t2⑥
t＝t2－t1⑦
联立④⑥⑦解得t＝20 s⑧
（3）设汽车到斑马线时的速度为v，在汽车刹车过程中
由运动学有v22－v2＝2as⑨
联立①⑤⑨解得v＝55 m/s⑩
答案：（1）4 s 2.5×103 N （2）20 s （3）55 m/s关键词句
获取信息
汽车以v1＝12 m/s的速度朝收费站沿直线行驶
开始时汽车匀速正常行驶
过ETC通道，需要在距收费站中心线前d＝10 m处正好匀减速至v2＝4 m/s，匀速通过中心线后
先匀减速，然后匀速运动10 m
再匀加速至v1正常行驶
加速运动后匀速
如果过人工收费通道……正常行驶
匀减速到速度为零，停20 s，再加速
汽车加速和减速过程中的加速度大小均为1 m/s2
加速度大小已知
速度(m/s)
思考距离(m)
制动距离(m)
正常
酒后
正常
酒后
15
7.5
15.0
22.5
30.0
20
10.0
20.0
36.7
46.7
25
12.5
25.0
54.2
66.7