福建省漳州市2021-2022学年八年级下学期期末教学质量检测（华师大版B卷）数学试题（含答案）

这是一份福建省漳州市2021-2022学年八年级下学期期末教学质量检测（华师大版B卷）数学试题（含答案），共9页。试卷主要包含了选择题等内容，欢迎下载使用。
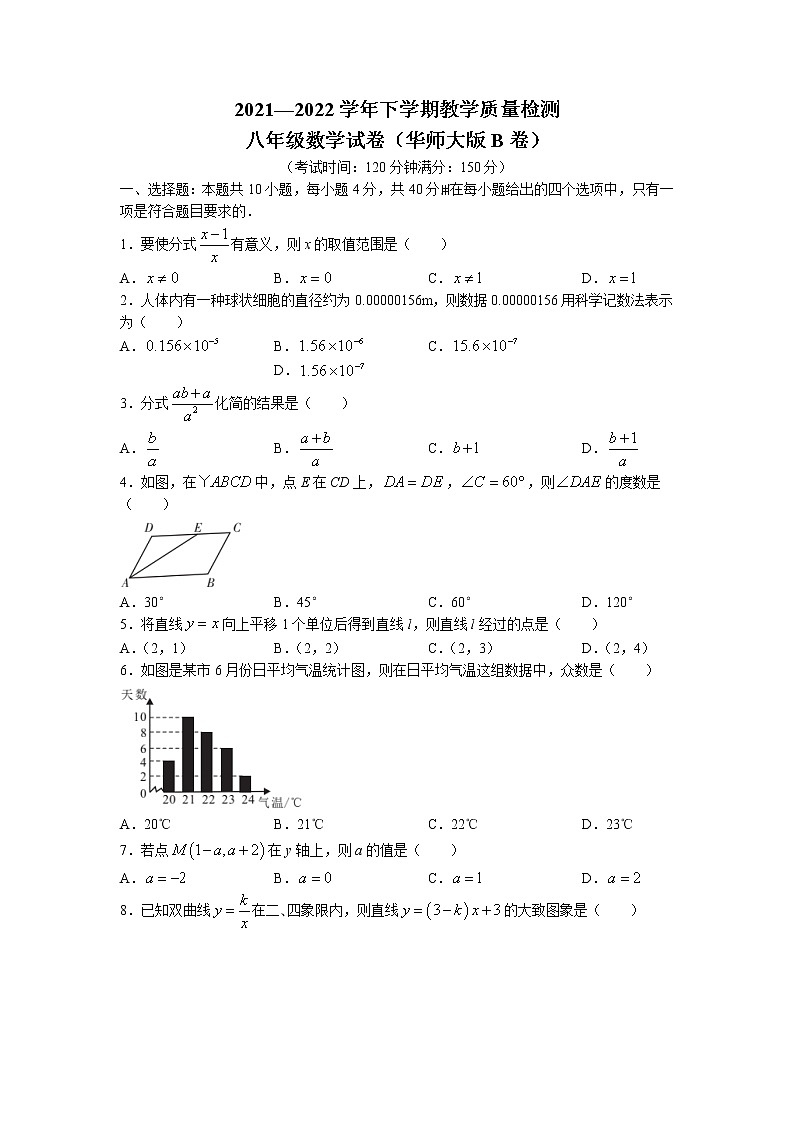
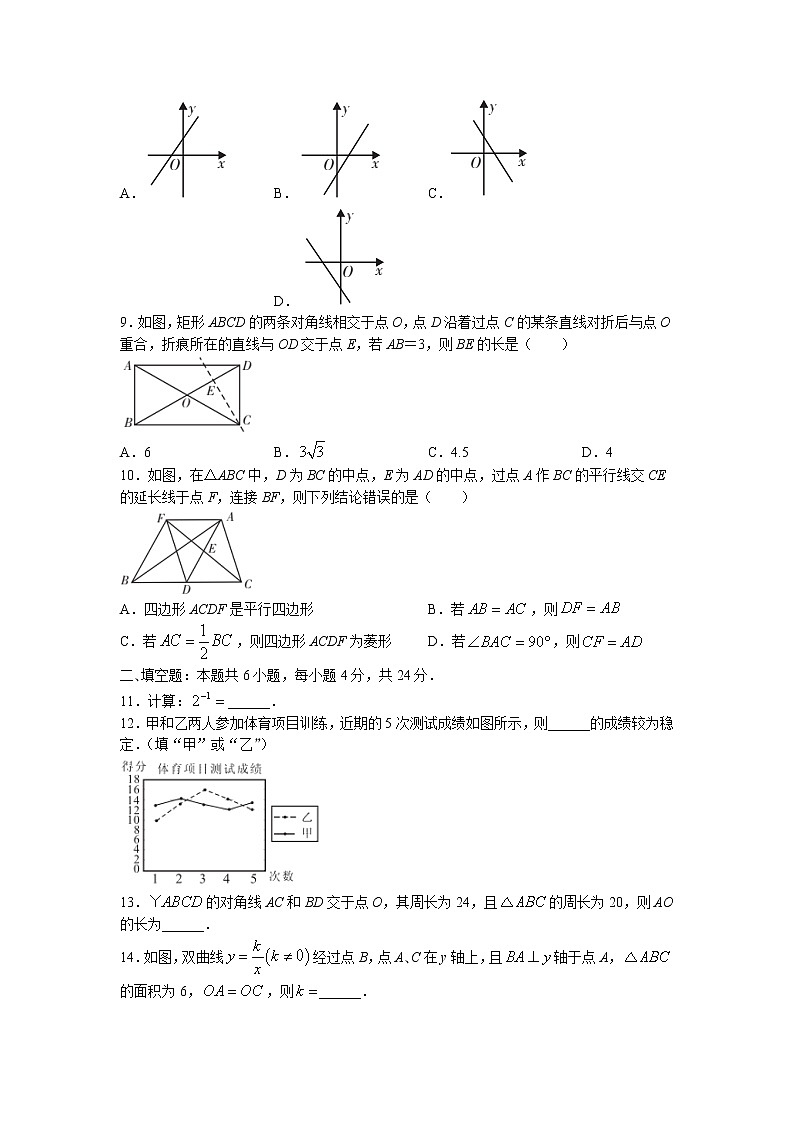
2021—2022学年下学期教学质量检测八年级数学试卷（华师大版B卷）（考试时间：120分钟满分：150分）一、选择题：本题共10小题，每小题4分，共40分ꎮ在每小题给出的四个选项中，只有一项是符合题目要求的．1．要使分式有意义，则x的取值范围是（    ）A． B． C． D．2．人体内有一种球状细胞的直径约为0.00000156m，则数据0.00000156用科学记数法表示为（    ）A． B． C． D．3．分式化简的结果是（    ）A． B． C． D．4．如图，在中，点E在CD上，，，则的度数是（    ）A．30° B．45° C．60° D．120°5．将直线向上平移1个单位后得到直线l，则直线l经过的点是（    ）A．（2，1） B．（2，2） C．（2，3） D．（2，4）6．如图是某市6月份日平均气温统计图，则在日平均气温这组数据中，众数是（    ）A．20℃ B．21℃ C．22℃ D．23℃7．若点在y轴上，则a的值是（    ）A． B． C． D．8．已知双曲线在二､四象限内，则直线的大致图象是（    ）A． B． C． D．9．如图，矩形ABCD的两条对角线相交于点O，点D沿着过点C的某条直线对折后与点O重合，折痕所在的直线与OD交于点E，若AB＝3，则BE的长是（    ）A．6 B． C．4.5 D．410．如图，在△ABC中，D为BC的中点，E为AD的中点，过点A作BC的平行线交CE的延长线于点F，连接BF，则下列结论错误的是（    ）A．四边形ACDF是平行四边形 B．若，则C．若，则四边形ACDF为菱形 D．若，则二､填空题：本题共6小题，每小题4分，共24分．11．计算：______．12．甲和乙两人参加体育项目训练，近期的5次测试成绩如图所示，则______的成绩较为稳定．（填“甲”或“乙”）13．的对角线AC和BD交于点O，其周长为24，且的周长为20，则AO的长为______．14．如图，双曲线经过点B，点A､C在y轴上，且轴于点A，的面积为6，，则______．15．如图，在菱形ABCD中，CD边的垂直平分线EF恰好经过点A，交CD于点E，连接BE，若，则AE的长为______．16．如图，点E在正方形ABCD的边BC上，BE＝2，EC＝4，将△ABE沿AE折叠得到△AFE，延长EF交DC于点G，连接AG．现给出以下结论：①②③④其中正确的结论是______．（写出所有正确结论的序号）三､解答题：本题共9小题，共86分。解答应写出文字说明､证明过程或演算步骤。17．（8分）解方程：．18．（8分）如图，在中，点E､F在对角线AC上，且AE＝CF．求证：∠ABE＝∠CDF．19．（8分）先化简，再求值：，其中．20．（8分）如图，双曲线经过的顶点和顶点．（1）求m的值．（2）求直线AB的函数表达式．21．（8分）网课期间，为提高教学质量，某校对所有班级进行线上教学评比，最终决定从甲､乙两班中选出一个线上教学先进班集体，下表是这两个班级在四个方面的得分（单位：分）．班级课堂质量线上答疑作业提交师生互动甲班10710a乙班9b98已知甲班在四个方面得分的中位数为9.5分，乙班在四个方面得分的平均数为9分．（1）填空：______，______；（2）如果以上四个方面的重要性之比为3∶2∶2∶3，请你通过计算判断，哪个班级被选为线上教学先进班集体？22．（10分）如图，矩形ABCD的两条对角线相交于点O．（1）在CD边上求作点E，使得；（要求：尺规作图，保留作图痕迹，不写作法）（2）在（1）的条件下，延长EO交AB于点F，连接DF，求证：四边形BEDF是菱形．23．（10分）某企业准备购买一批防护服赠送一线抗疫人员，经了解，购进5套甲种防护服和4套乙种防护服需要2000元，购进10套甲种防护服和3套乙种防护服需要3000元．（1）求甲种防护服和乙种防护服每套各多少元?（2）实际购买时，厂家推出优惠方案：购买甲种防护服超过40套时，超过的部分按原价的8折付款，乙种防护服没有优惠．该企业打算购买这两种防护服共300套，已知甲种防护服的数量超过40套，但不超过乙种防护服的数量的2倍．①求该企业所花的费用w（元）与甲种防护服的数量a（套）的函数关系式；②求该企业所花费用的最小值．24．（12分）已知直线．（1）求当和时，两条直线的交点A的坐标；（2）若反比例函数的图象与直线交于点A和另外一点．①求b的值；②若m､n均为整数，求a的值．25．（14分）【性质探究】（1）如图1，在中，，AB＝AC，点D在斜边BC上，将△ABD绕点A逆时针旋转90°得到△ACE．①直线BD与CE的位置关系为______；②若点F为BE的中点，连接AF，请探究线段AF与CD的数量关系，并给予证明．【拓展应用】（2）如图2，已知点E是正方形ABCD的边BC上任意一点，以AE为边作正方形AEFG，连接BG，点H为BG的中点，连接AH．若AB＝4，BE＝3，求AH的长． 2021—2022学年下学期教学质量检测八年级数学参考答案及评分意见（华师大版B卷）一､选择题（共10小题，每小题4分，满分40分）题号12345678910答案ABDACBCACD二､填空题：本题共6小题，每小题4分，共24分。11．12．甲    13．4    14．6    15．    16．①②③三､解答题：本题共9小题，共86分ꎮ17．（8分）解：3x－3＝2x．3x－2x＝3．x＝3．经检验，x＝3是原方程的解．∴原方程的解是x＝3．18．（8分）证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∴∠DAC＝∠BCA，又AE＝CF，∴△ADE≌△CBF，∴DF＝BE，∠DFA＝∠BEC，∴，∴四边形BEDF是平行四边形．19．（8分）解：原式．当时，原式．20．（8分）解：（1）将点代入，得；（2）∵m＝12，∴双曲线为．∵点B在双曲线上，∴，解得，∴点B为．设直线AB的函数表达式为，根据题意，得解这个方程组，得∴直线AB的函数表达式为．21．（8分）解：（1）a＝9，b＝10；（2）甲班得分：．乙班得分：∵，∴甲班被选为线上教学先进班集体．22．（10分）解：（1）正确完成作图．∴点E为所求作的点．（2）∵四边形ABCD是矩形，∴DO＝OB，，∴∠CDB＝∠ABD，又∠DOE＝∠BOF，∴△DOE≌△BOF．∴DE＝BF，∴四边形BEDF是平行四边形．由（1）得EF⊥BD，∴是菱形．23．（10分）解：（1）设甲种防护服每套x元，乙种防护服每套y元．根据题意，得解得答：甲种防护服每套240元，乙种防护服每套200元．4分（2）①．∴w与a的函数关系式是．②∵甲种防护服的数量超过40套，但不超过乙种防护服的数量的2倍，∴解得．∵，，∴w随a的增大而减少．∴当时，w取得最小值为60320．答：该企业所花费用的最小值为60320元．24．（12分）解：（1）当时，直线为．当时，直线为．解方程组得∴点A的坐标为．（2）①∵反比例函数的图象经过点A，∴，解得b＝2．②∵b＝2，∴反比例函数为．∵点在反比例函数的图象上，∴．∵m､n均为整数，∴m＝1，n＝2或m＝2，n＝1或m＝－2，n＝－1或m＝－1，n＝－2．当m＝1，n＝2时，2＝a＋a－2，解得a＝2，当m＝2，n＝1时，1＝2a＋a－2，解得a＝1，当m＝－2，n＝－1时，－1＝－2a＋a－2，解得a＝－1，当m＝－1，n＝－2时，与点A重合，不合题意，舍去．∴a的值为2或1或－1．25．（14分）解：（1）①
②延长BA至点G，使AG＝AB，连接GE，∵将△ABD绕点A逆时针旋转90°得到△ACE，∴∠DAE＝∠BAC＝90°，AE＝AD，AC＝AB＝AG，又∠DAC=90°－∠CAE=∠GAE，∴△ADC≌△AEG，∴CD＝GE．延长FA至点Q，使AQ＝AF，连接GQ，∵AG＝AB，∠BAF＝∠GAQ，∴△ABF≌△AGQ，∴∠BFA＝∠GQA，BF＝GQ，∴，即．∵点F为BE的中点，∴EF＝BF＝GQ，∴四边形EFQG是平行四边形，∴QF＝GE．∵，CD＝GE，∴．（2）如图，连接DE､DG，∵四边形ABCD和四边形AEFG为正方形，∴AB＝AD，AE＝AG，∠BAD＝∠EAG＝90°，又∠BAE＝90°－∠EAD＝∠DAG，∴△BAE≌△DAG，∴△DAG可以由△BAE绕点A逆时针旋转90°得到．∵AB＝4，BE＝3，∴CE＝1，CD＝4．由（1）中②可知，∴．