2022年人教版北京朝阳区第12章 全等三角形章末检测有答案

这是一份2022年人教版北京朝阳区第12章 全等三角形章末检测有答案，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
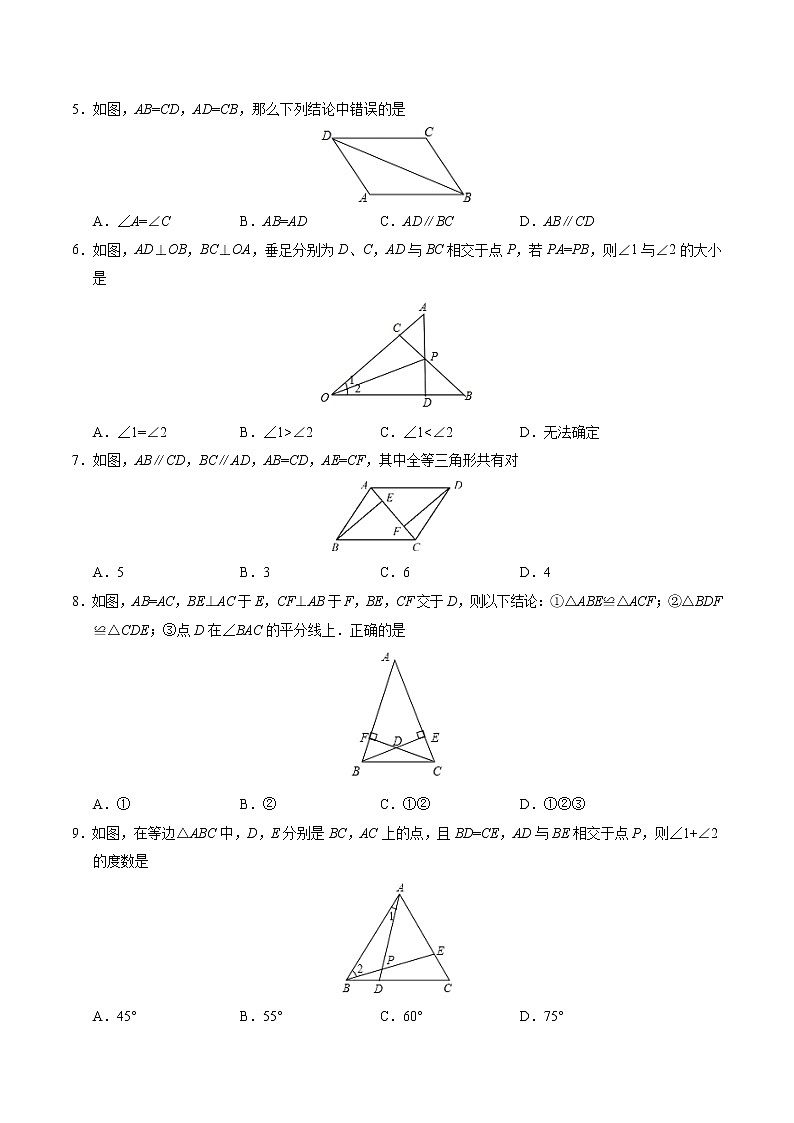
(时间：90分钟  满分：120分)一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．下列作图属于尺规作图的是A．用量角器画出∠AOB，使∠AOB等于已知角αB．用圆规和直尺作线段AB，使AB等于已知线段αC．用刻度尺作出线段AB等于2倍的已知线段mD．用三角板作45°的角2．如图，某同学不小心把一块三角形玻璃打碎成三块，现在要到玻璃店配一块与原来完全相同的玻璃，最省事的方法是A．带①和②去       B．只带②去C．只带③去        D．都带去3．山脚下有A、B两点，要测出A、B两点间的距离．在地上取一个可以直接到达A、B点的点C，连接AC并延长到D，使CD=CA．连接BC并延长到E，使CE=CB，连接DE．可以证△ABC≌△DEC，得DE=AB，因此，测得DE的长就是AB的长，判定△ABC≌△DEC的理由是A．SSS    B．ASA    C．SAS    D．AAS4．下列条件中，能判定△ABC≌△DEF的是A．AB=DE，BC=EF，∠A=∠E    B．∠A=∠E，AB=EF，∠B=∠DC．∠A=∠D，∠B=∠E，∠C=∠F   D．∠A=∠D，∠B=∠E，AC=DF5．如图，AB=CD，AD=CB，那么下列结论中错误的是A．∠A=∠C   B．AB=AD   C．AD∥BC   D．AB∥CD6．如图，AD⊥OB，BC⊥OA，垂足分别为D、C，AD与BC相交于点P，若PA=PB，则∠1与∠2的大小是A．∠1=∠2   B．∠1>∠2   C．∠1<∠2   D．无法确定7．如图，AB∥CD，BC∥AD，AB=CD，AE=CF，其中全等三角形共有对A．5     B．3    C．6    D．48．如图，AB=AC，BE⊥AC于E，CF⊥AB于F，BE，CF交于D，则以下结论：①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上．正确的是A．①    B．②    C．①②    D．①②③9．如图，在等边△ABC中，D，E分别是BC，AC上的点，且BD=CE，AD与BE相交于点P，则∠1+∠2的度数是A．45°    B．55°    C．60°    D．75°10．如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，则下列结论：①DA平分∠CDE；②∠BAC=∠BDE；③DE平分∠ADB；④BE+AC=AB，其中正确的有A．4个         B．3个C．2个         D．1个二、填空题（本大题共10小题，每小题3分，共30分）11．若△ABC≌△A′B′C′，AB=3，∠A′=30°，则A′B′=__________，∠A=__________°．12．如图，为的平分线，，，则点到射线的距离为__________．13．已知△ABC≌△DEF，且△ABC的三边长分别为3，4，5，则△DEF的周长为__________．14．如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是__________．15．如图，在Rt△ABC中，∠ACB=90°，BC=2 cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F．若EF=8 cm，则AE=__________cm．16．如图，△ABC中，D是AB的中点，DE⊥AB，∠ACE+∠BCE=180°，EF⊥AC交AC于F，AC=12，BC=8，则AF=________．17．如图，Rt△ABC中，∠C=90°，BD平分∠ABC交边AC于点D，CD=4，△ABD的面积为10，则AB的长是__________．18．如图，AB=AC，AD=AE，∠BAC=∠DAE，点D在线段BE上．若∠1=25°，∠2=30°，则∠3=__________．19．如图，五边形ABCDE中，∠B=∠E=90°，AB=CD=AE=BC+DE=2，则这个五边形ABCDE的面积是__________．20．如图，Rt△中，，分别是上的动点，且，当=__________时，才能使和全等．三、解答题（本大题共8小题，共60分．解答应写出文字说明、证明过程或演算步骤）21．如图，已知∠1=∠2，∠B=∠D，求证：CB=CD．    22．如图，点E，F在AB上，CE与DF交于点G，AD=BC，∠A=∠B，AE=BF．求证：GE=GF．    23．如图，．求证：．    24．如图，在Rt△ABC中，∠C=90°．作∠BAC的平分线AP交边BC于点D．（保留作图痕迹，不写作法）．若∠BAC=28°，求∠ADB的度数．   25．如图，是的平分线，点在上，且，交于点．试说明：平分．   26．如图，在△BCE中，AC⊥BE，AB=AC，点A、点F分别在BE、CE上，BE、CF相交于点D，BD=CE．求证：AD=AE．    27．如图，四边形ABCD中，对角线AC、BD交于点O，AB=AC，点E是BD上一点，且AE=AD，∠EAD=∠BAC．（1）求证：∠ABD=∠ACD；（2）若∠ACB=65°，求∠BDC的度数．    28．如图，△ABC是边长为5 cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿射线AB，BC运动，且它们的速度都为2 cm/s．设点P的运动时间为t（s）．（1）当t为何值时，△ABQ≌△CBP；（2）连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．     3．【答案】C【解析】因为CD=CA，CE=CB，，所以△ABC≌△DEC（SAS）．故选C．4．【答案】D 【解析】A．AB=DE，BC=EF，∠A=∠E，SSA不能确定全等；B．∠A=∠E，AB=EF，∠B=∠D，AB和EF不是对应边，不能确定全等；C．∠A=∠D，∠B=∠E，∠C=∠F，AAA不能确定全等；D．∠A=∠D，∠B=∠E，AC=DF，根据AAS，能判断△ABC≌△DEF．故选D．5．【答案】B【解析】∵在△ABD和△CDB中，，∴△ABD≌△CDB，∴∠ADB=∠CBD，∠ABD=∠CDB，∠A=∠C，∴AD∥BC，AB∥CD，∴A、C、D选项正确．故选B．6．【答案】A【解析】∵AD⊥OB，BC⊥OA，垂足分别为D、C，AD与BC相交于点P，PA=PB，∠CPA=∠DPB，∴△CPA≌△∠DPB（AAS），∴PC=PD，∴∠1=∠2，故选A．7．【答案】B【解析】根据AB=CD，AE=CF，∠BAE=∠DCF可得：△ABE≌△CDF；根据CE=AF，∠DAF=∠BCE，∠DFA=∠BEC可得：△ADF≌△CBE；根据∠DAC=∠BCA，∠BAC=∠DCA，AC=CA可得：△ACD≌△CAB，共有3对全等三角形，故选B．8．【答案】D∵△ABE≌△ACF，∴AE=AF，∵△BDF≌△CDE，∴DF=DE，∵在△AFD和△AED中，，∴△AFD≌△AED（SSS），∴∠FAD=∠EAD，∴AD平分∠BAC，即点D在∠BAC的平分线上．综上所述，在本题给出的结论中，正确的是①②③．故选D．9．【答案】C【解析】∵在等边△ABC中，∠ABC=∠C=60°，AB=BC，BD=CE，∴△ABD≌△BCE，∴∠CBE=∠1，而∠CBE+∠2=60°，∴∠1+∠2=60°．故选C．10．【答案】B【解析】根据题中条件，结合图形及角平分线的性质得到：∵AD平分∠BAC，∴∠DAC=∠DAE，∵∠C=90°，DE⊥AB，∴∠C=∠E=90°，∵AD=AD，∴△DAC≌△DAE，∴∠CDA=∠EDA，∴①AD平分∠CDE正确；无法证明∠BDE=60°，∴③DE平分∠ADB错误；∵BE+AE=AB，AE=AC，∴BE+AC=AB，∴④BE+AC=AB正确；∵∠BDE=90°-∠B，∠BAC=90°-∠B，∴∠BDE=∠BAC，∴②∠BAC=∠BDE正确．故选B．11．【答案】3；30【解析】由对应角相等，对应边相等，A′B′=AB，∠A=30°．故答案为：3；30．12．【答案】3【解析】如图，过C作CF⊥AO．∵OC为∠AOB的平分线，CM⊥OB，∴CM=CF．∵CM=3，∴CF=3．故答案为：3．角的余角相等），在△FCE和△ABC中，，∴△ABC≌△FCE（ASA），∴AC=EF，∵AE=AC-CE，BC=2 cm，EF=8 cm，∴AE=8-2=6 cm，故答案为：6．16．【答案】10【解析】如图，连接AE，BE，过E作EG⊥BC于G，∵D是AB的中点，DE⊥AB，∴DE垂直平分AB，∴AE=BE，∵∠ACE+∠BCE=180°，∠ECG+∠BCE=180°，∴∠ACE=∠ECG，又∵EF⊥AC，EG⊥BC，∴EF=EG，∠FEC=∠GEC，∵CF⊥EF，CG⊥EG，∴CF=CG，在Rt△AEF和Rt△BEG中，，∴Rt△AEF≌Rt△BEG（HL），∴AF=BG，设CF=CG=x，则AF=AC-CF=12-x，BG=BC+CG=8+x，∴12-x=8+x，解得x=2，∴AF=12-2=10．故答案为：10．17．【答案】5【解析】如图，过点D作DE⊥AB于点E．∵BD平分∠ABC．又∵DE⊥AB，DC⊥BC，∴DE=DC=4．∵△ABD的面积=·AB·DE=×AB×4=10，∴AB=5．故答案为：5．20．【答案】3或8【解析】分为两种情况：①当AP=3时，∵BC=3，∴AP=BC，∵∠C=90°，AE⊥AC，∴∠C=∠QAP=90°，∴在Rt△ABC和Rt△QAP中，，∴Rt△ABC≌Rt△PQA（HL）；②当AP=8时，∵AC=8，∴AP=AC，∵∠C=90°，AE⊥AC，∴∠C=∠QAP=90°，∴在Rt△ABC和Rt△QAP中，，∴Rt△ABC≌Rt△QAP（HL），故答案为：3或8． 22．【解析】∵AE=BF，∴AE+EF=BF+EF，∴AF=BE，在△ADF与△BCE中，，∴△ADF≌△BCE（SAS），∴∠CEB=∠DFA，∴GE=GF．23．【解析】∵，∴，即，在和中，，∴≌（SAS），∴．24．【解析】（1）如下图所示，AD为所求的角平分线：（2）∵∠BAC的平分线AP，∠BAC=28°，∴∠CAD=BAD=14°，又∵∠C=90°，∠ADB=∠C+∠CAD，∴∠ADB=90°+14°=104°．26．【解析】∵AC⊥BE，∴∠BAD=∠CAE=90°，在Rt△ABD和Rt△ACE中，，∴Rt△ABD≌Rt△ACE（HL），∴AD=AE．27．【解析】（1）∵∠BAC=∠EAD，∴∠BAC-∠EAC=∠EAD-∠EAC，即：∠BAE=∠CAD，在△ABE和△ACD中，，28．【解析】（1）∵△ABQ≌△CBP，∴BQ=BP，∴2t=5-2t，∴t=，∴t= s时，△ABQ≌△CBP，（2）结论：∠CMQ=60°不变，理由：∵△ABC是等边三角形，∴∠ABQ=∠CAP，AB=CA，又∵点P，Q运动速度相同，∴AP=BQ，在△ABQ与△CAP中，， ∴△ABQ≌△CAP（SAS），∴∠BAQ=∠ACP，∵∠QMC=∠ACP+∠MAC，∴∠CMQ=∠BAQ+∠MAC=∠BAC=60°．