数学必修 第一册3.2 函数的基本性质第2课时导学案

这是一份数学必修 第一册3.2 函数的基本性质第2课时导学案，文件包含321单调性与最大小值第2课时导学案原卷版docx、321单调性与最大小值第2课时导学案答案版docx等2份学案配套教学资源，其中学案共17页， 欢迎下载使用。
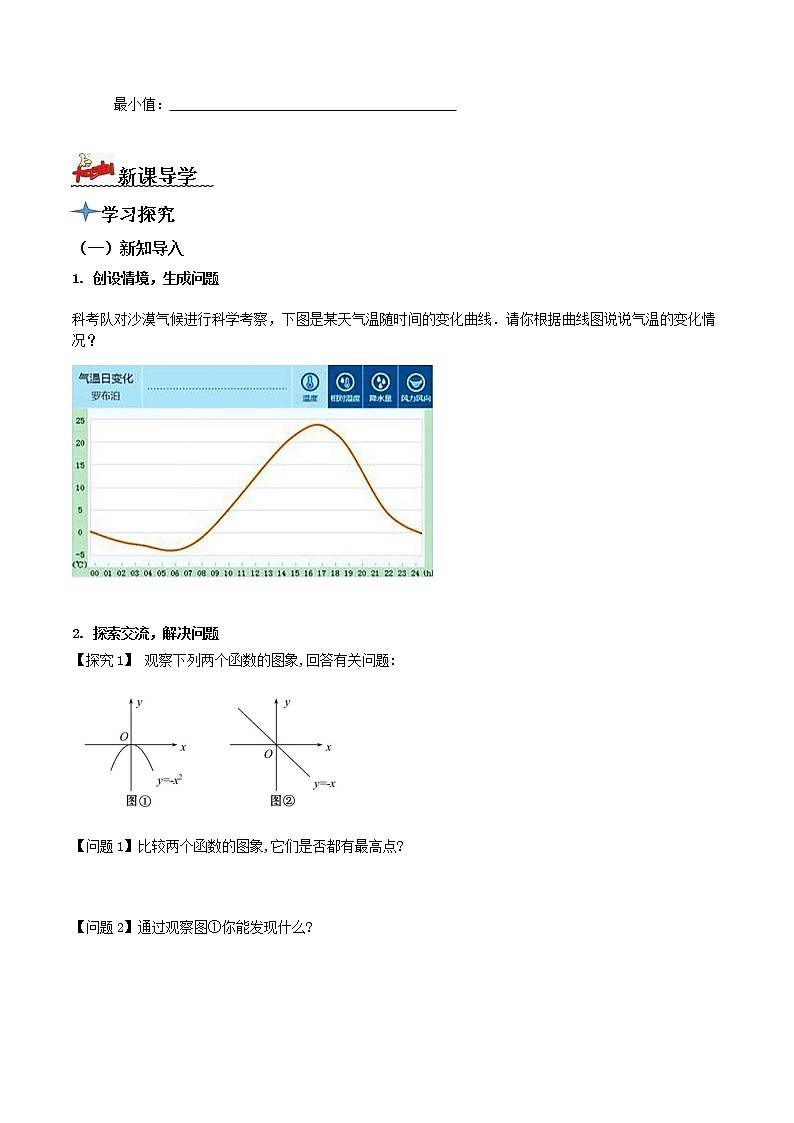
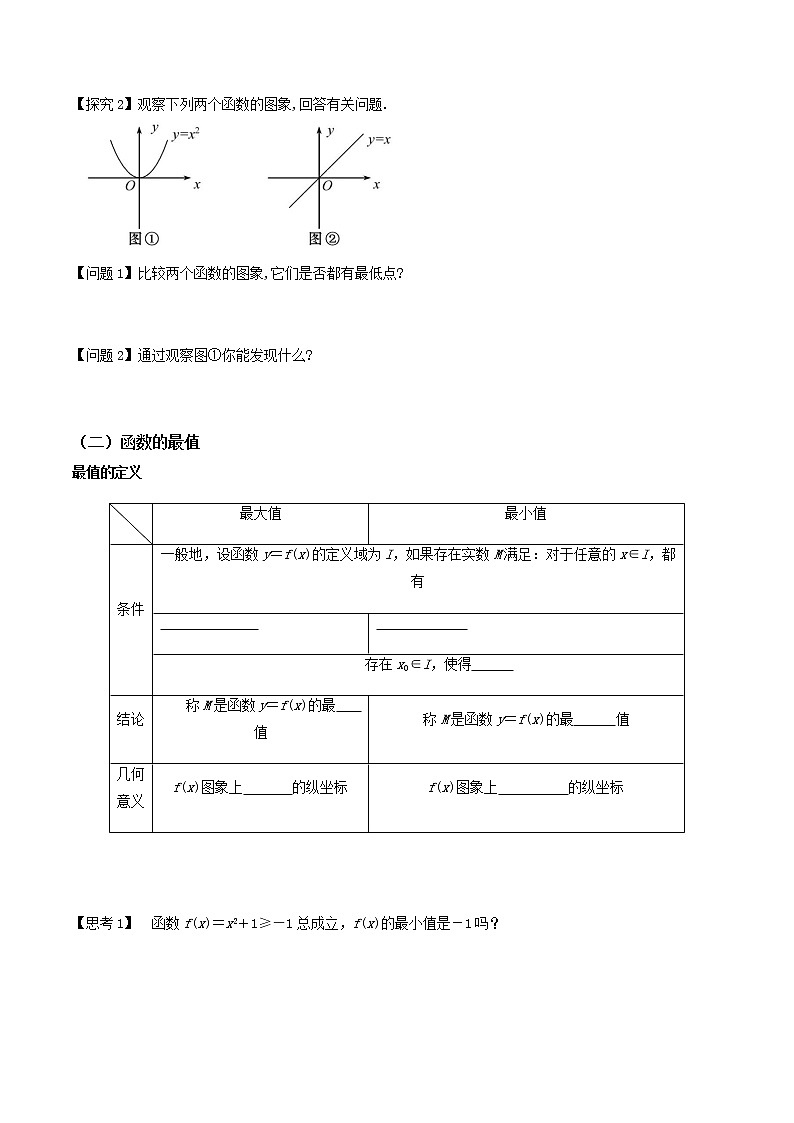
《3.2.1单调性与最大（小）值》第2课时  函数的最值 导学案         参考答案新课导学  （一）新知导入【提示】气温从0时逐渐降底，6时气温达到最低，从6时到17时，气温逐渐升高，17时气温达到最高，从17时到24时，气温逐渐降低。 【问题1】图①中函数y=的图象上有一个最高点;图②中函数y=-x的图象上没有最高点.【问题2】对任意x∈R,都有f(x)≤f(0)，f(0)是最大值。【问题3】图①中函数y=的图象有一个最低点.图②中函数y=x的图象没有最低点. 【问题4】对任意x∈R都有f(x)≥f(0)，f(0)是最小值。（二）函数的最值最值的定义   f(x)≤M        f(x0)＝M      大     最高点       f(x)≥M        小       最低点  【思考1】　　f(x)的最小值不是－1，因为f(x)取不到－1.  （三）利用图象求函数的最值【例1】【解】　作出f(x)的图象如图：由图象可知，当x＝2时，f(x)取最大值为2；当x＝时，f(x)取最小值为－.所以f(x)的最大值为2，最小值为－.根据图象可知，函数在区间(－∞，－1]，[0,1]上是增函数；函数在区间(－1,0)，(1，＋∞)上是减函数．  【巩固练习1】  【解】　y＝－|x－1|＋2＝图象如图所示，由图象知，函数y＝－|x－1|＋2的最大值为2，没有最小值，所以其值域为(－∞，2]．（四）利用单调性求最值例2. 【解】　设x1，x2是[－4,0]上的任意两个实数，且x1＜x2，则f(x1)－f(x2)＝－x1－＋x2  ＝＋x2－x1.∵－4≤x1＜x2≤0，∴x1－x2＜0，x1＋x2＜0，x2－x1＞0，∴f(x1)－f(x2)＞0，即f(x1)＞f(x2)，∴f(x)在[－4,0]上是减函数．∴f(x)min＝f(0)＝3，f(x)max＝f(－4)＝9.[巩固练习2]  【解】法一：设x1，x2是区间[－3，－2]上的任意两个实数，且x1＜x2，则f(x1)－f(x2)＝－＝＝.由于－3≤x1＜x2≤－2，则x1－x2＜0，x1＋1＜0，x2＋1＜0.所以f(x1)－f(x2)＜0，f(x1)＜f(x2)．所以函数y＝，x∈[－3，－2]是增函数．又因为f(－2)＝4，f(－3)＝3，所以函数的最大值是4，最小值是3.法二：f(x)＝＝＝2＋，所以f(x)图象的对称中心是(－1,2)，在(－∞，－1)，(－1，＋∞)是增函数，图象如图：由图象可知f(x)在[－3，－2]的值域为[3,4]，最小值为f(－3)＝3，最大值为f(－2)＝4.（五）利用单调性比较大小、解不等式例3.　(1) 【解】由题意知，f(x)的对称轴为x＝2，故f(1)＝f(3)．∵f(x)＝x2＋bx＋c，∴f(x)在[2，＋∞)上为增函数．∴f(2)＜f(3)＜f(4)，即f(2)＜f(1)＜f(4)．(2) 【解】由题意可得解得0＜a＜1.①又f(x)在(－1,1)上是减函数，且f(1－a)＜f(2a－1)，∴1－a＞2a－1，即a＜.②由①②可知，0＜a＜， 即所求a的取值范围是.【巩固练习3】【解】∵f(x)是定义在(0，＋∞)上的减函数，且f(x)<f(2x－3)，∴解得<x<3.（六）函数最值的实际应用例4. 【解】　(1)由题意得G(x)＝2.8＋x，所以f(x)＝R(x)－G(x)＝(2)当x>5时，因为函数f(x)单调递减，所以f(x)<f(5)＝3.2(万元)，当0≤x≤5时，函数f(x)＝－0.4(x－4)2＋3.6，当x＝4时，f(x)有最大值为3.6(万元)，所以当工厂生产4百台产品时，可使盈利最大为3.6万元．【巩固练习4 】　将进货单价为40元的商品按50元一个出售时，能卖出500个，已知这种商品每涨价1元，其销售量就减少10个，为得到最大利润，售价应为多少元？最大利润为多少？【解】设售价为x元，利润为y元，单个涨价(x－50)元，销量减少10(x－50)个，销量为500－10(x－50)＝(1 000－10x)个，则y＝(x－40)(1 000－10x)＝－10(x－70)2＋9 000≤9 000.故当x＝70时，ymax＝9 000.即售价为70元时，利润最大值为9 000元．（七）二次函数最值问题例5.  【解】（1）f(x)=-2x+3=-4,对称轴为x=1,开口向上.f(x)在[-2,1]上递减,在[1,3]上递增,所以f(x)min=f(1)=-4,又因为f(-2)>f(3),所以f(x)max=f(-2)=5.（2）∵对称轴x＝1，①当1≥t＋2即t≤－1时，f(x)在[t，t＋2]上为减函数，∴f(x)min＝f(t＋2)＝(t＋2)2－2(t＋2)－3＝t2＋2t－3.②当t≤1<t＋2，即－1<t≤1时，f(x)min＝f(1)＝－4.③当1<t，即t>1时，f(x)在[t，t＋2]上为增函数，f(x)min＝f(t)＝t2－2t－3.设函数f(x)的最小值为g(t)，则有g(t)＝【巩固练习5】【解】因为f(x)=+2-,所以此二次函数图象的对称轴为x=a.(1)当a∈(-∞,-1)时,f(x)在[-1,+∞)上单调递增,所以f(x)min=f(-1)=2a+3.要使f(x)≥a恒成立,只需f(x)min≥a,即2a+3≥a,解得a≥-3,即-3≤a<-1.(2)当a∈[-1,+∞)时,f(x)min=f(a)=2-.要使f(x)≥a恒成立,只需f(x)min≥a,即2-≥a,解得-2≤a≤1,即-1≤a≤1.综上所述,实数a的取值范围为[-3,1]. （八）操作演练  素养提升[答案]  1.B   2.B   3.C    4.2