

江苏省苏州市吴中区2021-2022学年六年级下学期期末数学试卷(含答案)
展开
这是一份江苏省苏州市吴中区2021-2022学年六年级下学期期末数学试卷(含答案),共25页。试卷主要包含了判断题,选择题,计算题,填空题,操作题,解决问题等内容,欢迎下载使用。
2022年江苏省苏州市吴中区小升初数学试卷
一、判断题。(10分)
1.在一次植树活动中,种了100棵树,成活了93棵;后来又补种了7棵,全部成活。在这次活动中,树苗的成活率是100%。
2.一个等腰三角形,已知其中两条边的长度分别是6厘米和12厘米,则这个等腰三角形的周长可能是30厘米,也可能是24厘米。
3.一件商品出售时先降价20%,后又提价25%,现价和原价一样。
4.若甲×=乙÷=丙×(甲,乙、丙均不为0),那么最小的是丙。
5.一个三位小数,四舍五入到百分位是9.00,这个数最小是8.995。
6.甲、乙、丙三人分一箱水果,若按1:2:3或3:2:5的比分配都可以刚好分完,则这两种分法中,乙分得的一样多。
7.小明在教室里的位置可以用数对 (5,3)表示,他正前面的一个同学的位置用数对(4,3)表示. .
8.把一个平行四边形框架拉成一个长方形后,它的面积和周长都变大了。
9.两个圆锥的底面半径的比是1:2,高的比也是1:2,它们的体积比是1:4。
10.小琪抛一枚质地均匀的硬币,抛了10次,7次正面朝上,3次反面朝上,那么第11次抛硬币,正面朝上的可能性大。
二、选择题。(10分)
11.一个梯形如图,已知阴影部分的面积是12平方厘米,则梯形的面积是( )平方厘米。
A.16 B.18 C.20 D.28
12.一个圆柱和一个圆锥等底等高,若圆锥的高增加18分米,则圆柱和圆锥体积相等,原来圆柱的高是( )分米。
A.4 B.9 C.12 D.6
13.在含盐40%的盐水里,加入40克盐和100克水,这时盐水的含盐率( )
A.大于40% B.小于40% C.等于40% D.无法比较
14.小刚和小军买了相同价格的文具后,小刚还剩自己零花钱的,小军还剩自己零花钱的75%,小刚和小军两人原来的零花钱相比较,( )
A.小刚比小军多 B.小军比小刚多
C.一样多 D.无法比较
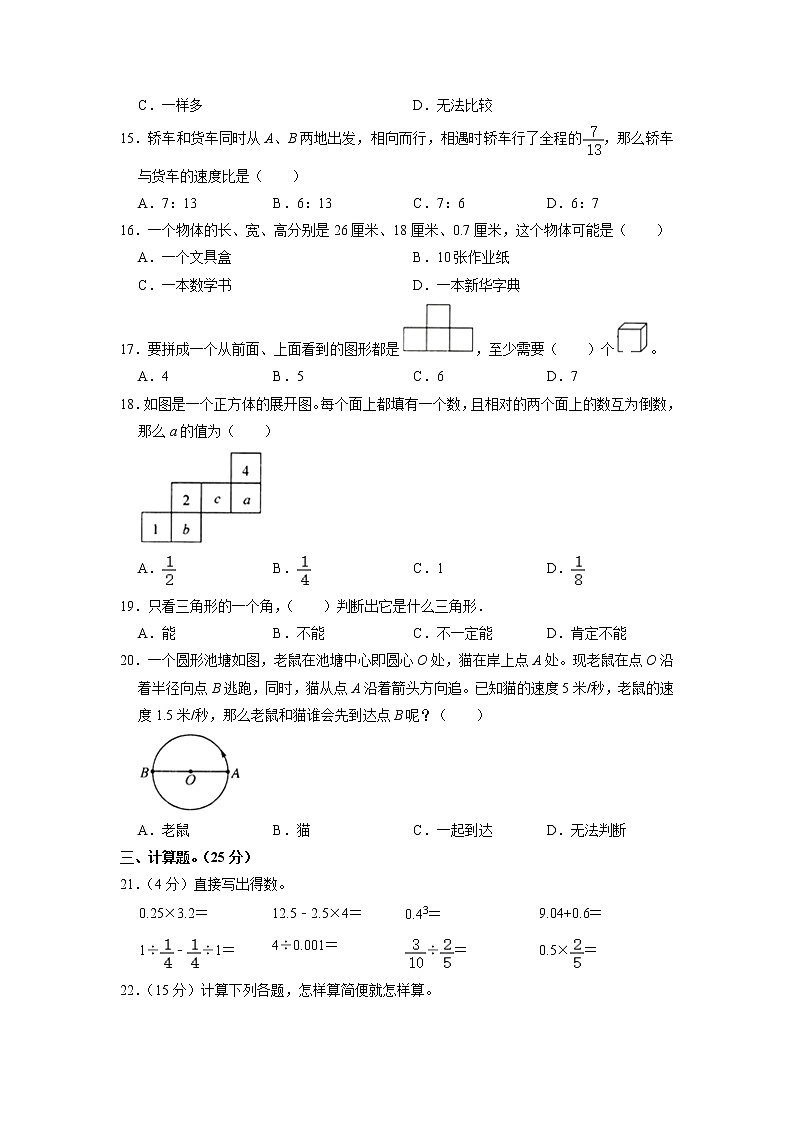
15.轿车和货车同时从A、B两地出发,相向而行,相遇时轿车行了全程的,那么轿车与货车的速度比是( )
A.7:13 B.6:13 C.7:6 D.6:7
16.一个物体的长、宽、高分别是26厘米、18厘米、0.7厘米,这个物体可能是( )
A.一个文具盒 B.10张作业纸
C.一本数学书 D.一本新华字典
17.要拼成一个从前面、上面看到的图形都是,至少需要( )个。
A.4 B.5 C.6 D.7
18.如图是一个正方体的展开图。每个面上都填有一个数,且相对的两个面上的数互为倒数,那么a的值为( )
A. B. C.1 D.
19.只看三角形的一个角,( )判断出它是什么三角形.
A.能 B.不能 C.不一定能 D.肯定不能
20.一个圆形池塘如图,老鼠在池塘中心即圆心O处,猫在岸上点A处。现老鼠在点O沿着半径向点B逃跑,同时,猫从点A沿着箭头方向追。已知猫的速度5米/秒,老鼠的速度1.5米/秒,那么老鼠和猫谁会先到达点B呢?( )
A.老鼠 B.猫 C.一起到达 D.无法判断
三、计算题。(25分)
21.(4分)直接写出得数。
0.25×3.2=
12.5﹣2.5×4=
0.43=
9.04+0.6=
1÷﹣÷1=
4÷0.001=
÷=
0.5×=
22.(15分)计算下列各题,怎样算简便就怎样算。
﹣+﹣
9×(+)﹣
×2+26÷
÷[(﹣)×]
(+﹣)
23.(6分)求未知数x。
x+=
x﹣25%x=15
x:18=:
四、填空题。(23分)
24.(4分)下面是一则关于月球的介绍,请你把“384401”、“﹣183”、“46亿”与“”填入相应的括号内;月球俗称月亮,在距今 年前就已经存在,它距离地球的平均距离为 千米;月球的昼夜温度差别很大,白天温度可达150℃;夜晚温度降到 ;月球引力仅相当于地球引力的 .
25.(2分)中秋节妈妈买了a盒月饼孝敬长辈,每盒75元,付给售货员500元,应找回 元,a的最大值是 。
26.(2分)如图中阴影部分占全长的,是 米。
27.(2分)中国农历中的“夏至”是一年中白昼最长、黑夜最短的一天.这一天,泰兴的白昼与黑夜时间比是7:5.这一天,泰兴的白昼是 小时,白昼时间比黑夜时间长 %.
28.(3分)45: =10÷8== %
29.(2分)一根绳子如果剪去它的,还剩4米,这根绳子原来长 米;如果这根绳子减去米,还剩 米。
30.用一根长60厘米的铁丝,搭一个长方体框架,搭成的长方体框架的长、宽、高是三个连续的自然数,那么搭成的长方体的体积是 立方厘米。
31.一个三角形三个内角的度数比是1:1:2,如果其中较短的边长5厘米,则这个三角形的面积是 平方厘米.
32.(2分)小明家果园里的枇杷树和杨梅树共有480棵,其中杨梅树的棵数是枇杷树的。枇杷树有 棵,杨梅树有 棵。
33.(2分)在一幅比例尺是1:3000000的地图上,量得A、B两地的距离是5厘米,A、B两地相距 千米。一辆轿车和一辆客车同时从两地相对开出,经过2小时相遇,轿车每小时行驶45千米,则客车每小时行 千米。
34.(2分)将如图1的正方形进行如下操作:第1次,分别连接对边中点,得到如图2的5个正方形;第2次,将图2左上角正方形按上述方法再分割,得到如图3的9个正方形。依此类推,第4次,同样的操作后会得到 个正方形。根据以上操作,若要得到101个正方形,需要操作 次。
五、操作题。(6分)
35.(2分)如图中一个小格的边长表示1千米,A点表示一家餐厅的位置。这家餐厅的送餐广告上说:本餐厅周边3千米的范围内免费送餐。
(1)请在图中表示出这家餐厅的送餐范围。
(2)小明家的位置用数对表示是(7,5),小红家的位置用数对表示是(5,9)。这家餐厅可以给 家免费送餐。(填“小明”或“小红”)
36.(4分)如图是一个长4厘米、宽2厘米的长方形。
(1)在长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形。
(2)这个梯形的面积是 平方厘米。
(3)以等腰直角三角形的一条直角边所在的直线为轴,将三角形旋转一周,可以形成一个 。
六、解决问题。(26分)
37.(4分)只列式或方程,不计算。
(1)王叔叔把20000元年终奖存入银行,定期两年,年利率为2.25%,到期后王叔叔一共可以取回多少元?
(2)眨眼有助于缓解眼睛疲劳,人在正常状态下每分钟眨眼30次,玩手机游戏时眨眼次数比正常状态下减少。玩手机游戏时每分钟眨眼多少次?
38.(4分)新冠疫情期间,某消毒液生产厂接到一批消毒液订单。工厂生产一周后,已完成与未完成的数量比为2:3,如果再生产18吨,那么正好完成这批订单的一半。这批消毒液订单一共有多少吨?
39.(4分)根据如图中提供的信息,求小花和小明各看了多少页。(列方程解答)
40.(4分)李师傅要制作一个无盖的圆柱形水桶,用下图所示的长方形铁皮做侧面,要使水桶的容积尽可能大。
(1)应该选用哪张正方形铁皮制作底面?(通过计算说明理由)
(2)这个水桶最多能装水多少升?
41.(4分)有64位同学去公园坐船,一共租了12条船,每条大船坐6人,每条小船坐4人,正好坐满。大船和小船各租了多少条?
42.(6分)学校环保志愿者对全校师生开展了“垃圾分类、从我做起”的抽样问卷调查,调查结果分析整理后,制作成以下两张统计图。其中丢垃圾行为分为以下几类:
A:能做到垃圾分类投放,并能向周边同学宣传垃圾分类相关知识。
B:能做到垃圾分类投放。
C:能把垃圾放垃圾桶,但不注意分类。
D:存在随手乱丢垃圾的行为。
请根据以上信息,解答下列问题。
(1)学校环保志愿者共调查了多少人?
(2)请将条形统计图补充完整。
(3)如果学校共有师生2200人,则存在随手乱丢垃圾行为的约有多少人?
2022年江苏省苏州市吴中区小升初数学试卷
参考答案与试题解析
一、判断题。(10分)
1.在一次植树活动中,种了100棵树,成活了93棵;后来又补种了7棵,全部成活。在这次活动中,树苗的成活率是100%。 ×
【分析】成活率=成活数量÷总数量×100%,据此计算即可。
【解答】解:(93+7)÷(100+7)×100%
=100÷107×100%
≈93%
答:树苗的成活率是93%。
故答案为:×。
2.一个等腰三角形,已知其中两条边的长度分别是6厘米和12厘米,则这个等腰三角形的周长可能是30厘米,也可能是24厘米。 ×
【分析】根据三角形的任意两边之和大于第三边,解答此题即可。
【解答】解:因为6+6=12,所以6厘米的边不能是腰。
12+12+6=30(厘米)
答:这个等腰三角形的周长是30厘米。
所以题干说法是错误的。
故答案为:×。
3.一件商品出售时先降价20%,后又提价25%,现价和原价一样。 √
【分析】一种商品先降价20%,把原价看作单位“1”,降价后是原价的(1﹣20%),再提价25%,是把降价后的价钱(1﹣20%)看作单位“1”,现价是原价的(1﹣20%)×(1+25%),据此解答即可。
【解答】解:(1﹣20%)×(1+25%)
=0.8×1.25
=1
因为1=1,所以现价和原价相等。
故答案为:√。
4.若甲×=乙÷=丙×(甲,乙、丙均不为0),那么最小的是丙。 ×
【分析】将甲×=乙÷=丙×化成甲×=乙×=丙×,再根据积的变化规律判断即可。
【解答】解:因为甲×=乙÷=丙×
所以甲×=乙×=丙×
<<,最小,所以乙最大。
原题说法错误。
故答案为:×。
5.一个三位小数,四舍五入到百分位是9.00,这个数最小是8.995。 √
【分析】要考虑9.00是一个三位小数的近似数,有两种情况:“四舍”得到的9.00最大是9.004,“五入”得到的9.00最小是8.995,由此解答问题即可。
【解答】解:“五入”得到的9.00最小是8.995。
所以原题说法正确。
故答案为:√。
6.甲、乙、丙三人分一箱水果,若按1:2:3或3:2:5的比分配都可以刚好分完,则这两种分法中,乙分得的一样多。 ×
【分析】单位”1“相同,在第一次分配中,乙占三分之一。第二次乙占五分之一。
【解答】解:1+2+3=6 2:6==
3+2+5=10 2:10==
>
故不一样多。
7.小明在教室里的位置可以用数对 (5,3)表示,他正前面的一个同学的位置用数对(4,3)表示. × .
【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,可知,小明在教室的位置是第5列,第3行,他前面的同学与他同列,行数减1,据此即可用数对表示出该同学的位置.
【解答】解:小明在教室的位置用数对表示是(5,3),他前面的一个同学的位置用数对表示是(5,2),所以原题说法错误.
故答案为:×.
8.把一个平行四边形框架拉成一个长方形后,它的面积和周长都变大了。 ×
【分析】把一个平行四边形框架拉成一个长方形,它的底没变,但是高变长了,所以面积变大了,四条边的长度没有变化,所以周长不变。
【解答】解:把一个平行四边形框架拉成一个长方形后,它的面积变大,周长不变。
所以题干说法是错误的。
故答案为:×。
9.两个圆锥的底面半径的比是1:2,高的比也是1:2,它们的体积比是1:4。 ×
【分析】半径比的平方是面积比,圆锥体积=底面积×高÷3,据此写出两个圆锥的体积比,化简即可。
【解答】解:12:22=1:4
(1×1÷3):(4×2÷3)=:=1:8
所以两个圆锥的底面半径的比是1:2,高的比也是1:2,它们的体积比是1:8;原题说法错误。
故答案为:×。
10.小琪抛一枚质地均匀的硬币,抛了10次,7次正面朝上,3次反面朝上,那么第11次抛硬币,正面朝上的可能性大。 ×
【分析】一枚硬币只有两个面,任意抛一次硬币,落地后正面朝上的可能性与反面朝上的可能性始终是相等的,所以无论前面几次的结果如何,第11次抛硬币,正面朝上的可能性与反面朝上的可能性相等。
【解答】解:因为任意抛一次硬币,落地后正面朝上的可能性与反面朝上的可能性始终是相等的,所以第11次抛硬币,正面朝上的可能性大,此题说法错误。
故答案为:×。
二、选择题。(10分)
11.一个梯形如图,已知阴影部分的面积是12平方厘米,则梯形的面积是( )平方厘米。
A.16 B.18 C.20 D.28
【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,把数据代入公式求出阴影部分三角形的高(梯形的高),再根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:12×2÷6
=24÷6
=4(厘米)
(8+6)×4÷2
=14×4÷2
=28(平方厘米)
答:梯形的面积是28平方厘米。
故选:D。
12.一个圆柱和一个圆锥等底等高,若圆锥的高增加18分米,则圆柱和圆锥体积相等,原来圆柱的高是( )分米。
A.4 B.9 C.12 D.6
【分析】根据体积与底面积都相等的圆锥的高是圆柱的高的3倍,解答此题即可。
【解答】解:18÷(3﹣1)
=18÷2
=9(厘米)
答:原来圆柱的高是9厘米。
故选:B。
13.在含盐40%的盐水里,加入40克盐和100克水,这时盐水的含盐率( )
A.大于40% B.小于40% C.等于40% D.无法比较
【分析】含盐率=盐的质量÷盐水质量×100%。求出加入盐水的含盐率,再与40%比较即可知道含盐率是上升还是下降。
【解答】解:40÷(40+100)×100%
=40÷140×100%
≈28.6%
28.6%<40%
答:这时盐水的含盐率小于40%。
故选:B。
14.小刚和小军买了相同价格的文具后,小刚还剩自己零花钱的,小军还剩自己零花钱的75%,小刚和小军两人原来的零花钱相比较,( )
A.小刚比小军多 B.小军比小刚多
C.一样多 D.无法比较
【分析】设文具价格为1,分别求出二人原有的零花钱即可。
【解答】解:设文具价格为1,则:
小刚原有的零花钱:1÷(1﹣)=
小军原有的零花钱:1÷(1﹣75%)=4
<4
所以小军原有的零花钱多。
故选:B。
15.轿车和货车同时从A、B两地出发,相向而行,相遇时轿车行了全程的,那么轿车与货车的速度比是( )
A.7:13 B.6:13 C.7:6 D.6:7
【分析】相遇时轿车行了全程的,货车行了全程的1﹣=,因为相遇时用的时间一样,所以轿车与货车的速度比等于它们所行的路程比:,货成最简整数比即可。
【解答】解::(1﹣)
=:
=7:6
答:轿车与货车的速度比是7:6。
故选:C。
16.一个物体的长、宽、高分别是26厘米、18厘米、0.7厘米,这个物体可能是( )
A.一个文具盒 B.10张作业纸
C.一本数学书 D.一本新华字典
【分析】根据长方体的特征,以及生活经验可知,一个物体的长、宽、高分别是26cm、18cm、0.7cm,这个物体可能数学书。据此解答。
【解答】解:一个长26厘米、宽18厘米、高0.7厘米的物体,最有可能是数学书。
故选:C。
17.要拼成一个从前面、上面看到的图形都是,至少需要( )个。
A.4 B.5 C.6 D.7
【分析】从正面、上面看到的形状都是,则下层至少4个,上层至少1个小正方体,在中间一列2个小正方体的任意一个上面均可。
【解答】解:4+1=5(个)
答:至少需要5个小正方体。
故选:B。
18.如图是一个正方体的展开图。每个面上都填有一个数,且相对的两个面上的数互为倒数,那么a的值为( )
A. B. C.1 D.
【分析】根据正方体的展平面展开图分析,可知a与2是两个相对的面,再根据题意和倒数的定义:乘积为1两个数互为倒数,分数里分子和分母相倒并且两数乘积为1的数就叫做倒数,即可求解。
【解答】解:根据正方体的展平面展开图分析,可知a与2互为倒数,2×=1,所以a是。
故选:A。
19.只看三角形的一个角,( )判断出它是什么三角形.
A.能 B.不能 C.不一定能 D.肯定不能
【分析】如果这个角大于或等于90°,就可以判定是钝角或者直角三角形;如果小于90°,则不能;进而得出结论.
【解答】解:由分析知:只看三角形的一个角,不一定能判断出它是什么三角形;
故选:C.
20.一个圆形池塘如图,老鼠在池塘中心即圆心O处,猫在岸上点A处。现老鼠在点O沿着半径向点B逃跑,同时,猫从点A沿着箭头方向追。已知猫的速度5米/秒,老鼠的速度1.5米/秒,那么老鼠和猫谁会先到达点B呢?( )
A.老鼠 B.猫 C.一起到达 D.无法判断
【分析】根据圆的周长公式:C=2πr,把数据代入公式求出圆周长的一半,也就是猫需要跑的距离,老鼠跑的距离就是圆的半径,根据时间=路程÷速度,分别求出各自需要的时间,然后进行比较,用时间少先到达。
【解答】解:设圆形水池的半径为r米,
πr÷5=(秒)
r÷1.5=r(秒)
<r
答:猫会先到达B点。
故选:B。
三、计算题。(25分)
21.(4分)直接写出得数。
0.25×3.2=
12.5﹣2.5×4=
0.43=
9.04+0.6=
1÷﹣÷1=
4÷0.001=
÷=
0.5×=
【分析】根据小数乘法、小数除法、数的立方、小数加法、分数乘法、除法以及分数、小数四则混合运算的法则直接写出得数即可。
【解答】解:
0.25×3.2=0.8
12.5﹣2.5×4=2.5
0.43=0.064
9.04+0.6=9.64
1÷﹣÷1=3
4÷0.001=400
÷=
0.5×=0.2
22.(15分)计算下列各题,怎样算简便就怎样算。
﹣+﹣
9×(+)﹣
×2+26÷
÷[(﹣)×]
(+﹣)
【分析】(1)根据加法交换律和减法的性质进行简算;
(2)根据乘法分配律和加法结合律进行简算;
(3)根据乘法分配律进行简算;
(4)先算小括号里的减法,再算中括号里的乘法,最后算括号外的除法;
(4)根据乘法分配律进行简算。
【解答】解:(1)
=()﹣()
=
=
(2)9×()﹣
=9×
=8+()
=8+1
=9
(3)
=×
=
=
=8
(4)÷[(﹣)×]
=÷[×]
=
=4
(5)(+﹣)
=(+﹣)×24
=
=8+6﹣4
=10
23.(6分)求未知数x。
x+=
x﹣25%x=15
x:18=:
【分析】(1)首先根据等式的性质,两边同时减去,然后两边再同时乘即可。
(2)首先化简,然后根据等式的性质,两边同时除以0.75即可。
(3)首先根据比例的基本性质化简,然后根据等式的性质,两边同时乘即可。
【解答】解:(1)x+=
x+﹣=﹣
x=
x×=×
x=
(2)x﹣25%x=15
0.75x=15
0.75x÷0.75=15÷0.75
x=20
(3)x:18=:
x=18×
x=12
x×=12×
x=
四、填空题。(23分)
24.(4分)下面是一则关于月球的介绍,请你把“384401”、“﹣183”、“46亿”与“”填入相应的括号内;月球俗称月亮,在距今 46亿 年前就已经存在,它距离地球的平均距离为 384401 千米;月球的昼夜温度差别很大,白天温度可达150℃;夜晚温度降到 ﹣183℃ ;月球引力仅相当于地球引力的 .
【分析】根据生活经验、对计量单位大小的认识和数据的大小,可知月球在距今46亿年前就已经存在,月球距离地球的平均距离为384401千米;月球上白天温度可达150℃,夜晚温度降到﹣183℃;月球引力仅相当于地球引力的.据此进行选择并填空即可.
【解答】解:月球俗称月亮,在距今46亿年前就已经存在,它距离地球的平均距离为384401千米;
月球的昼夜温度差别很大,白天温度可达150℃,夜晚温度降到﹣183℃;
月球引力仅相当于地球引力的.
故答案为:46亿,384401,﹣183,.
25.(2分)中秋节妈妈买了a盒月饼孝敬长辈,每盒75元,付给售货员500元,应找回 (500﹣75a) 元,a的最大值是 6 。
【分析】先根据“单价×数量=总价”求得花的钱数,再根据“付出的钱数﹣花的钱数=找回的钱数”进行解答即可。求a的最大值用500除以75求出的结果用去尾法求值。
【解答】解:500﹣75×a=500﹣75a(元)
a的最大值是:500÷75=6(个)≈6(个)
答:应找回(500﹣75a)元,则a的最大值是6。
故答案为:(500﹣75a),6。
26.(2分)如图中阴影部分占全长的,是 米。
【分析】把4m看作单位“1”,把它平均分成5份,其中的1份是,再根据一个数乘分数的意义,用4m乘,可以计算出阴影部分的长度。
【解答】解:如图中阴影部分占全长的。
答:图中阴影部分占全长的,是m。
故答案为:;。
27.(2分)中国农历中的“夏至”是一年中白昼最长、黑夜最短的一天.这一天,泰兴的白昼与黑夜时间比是7:5.这一天,泰兴的白昼是 14 小时,白昼时间比黑夜时间长 40 %.
【分析】泰兴的白昼与黑夜时间比是7:5,把白昼的时间看成7份,黑夜的时间看成5份,先求出白昼时间与黑时间的总份数,用24小时除以总份数,求出每份是多少小时,再乘7,即可求出白昼是多少小时;然后用白昼的份数减去黑夜的份数,求出白昼比黑夜长几份,再用长的分数除以黑夜的份数即可求解.
【解答】解:7+5=12
24÷12×7
=2×7
=14(小时)
(7﹣5)÷5
=2÷5
=40%
答:泰兴的白昼是 14小时,白昼时间比黑夜时间长 40%.
故答案为:14,40.
28.(3分)45: 36 =10÷8== 125 %
【分析】根据分数与除法的关系,10÷8=,将此分数化简是;根据比与分数的关系,=5:4,再根据比的基本性质比的前、后项都乘9就是45:36;10÷8=1.25,把1.25的小数点向右移动两位添上百分号就是125%。
【解答】解:45:36=10÷8==125%
故答案为:36,5,125。
29.(2分)一根绳子如果剪去它的,还剩4米,这根绳子原来长 10 米;如果这根绳子减去米,还剩 9.4 米。
【分析】把这根绳子原来的长看作单位“1”,剪去它的,还剩(1﹣),已知还剩4米,根据分数除法的意义,用4米除以(1﹣),就是这根绳子原来的长度;再用这根绳子原来的长度减米,就是还剩的长度。
【解答】解:4÷(1﹣)
=4÷
=10(米)
10﹣=9.4(米)
答:这根绳子原来长10米;如果这根绳子减去米,还剩9.4米。
故答案为:10,9.4。
30.用一根长60厘米的铁丝,搭一个长方体框架,搭成的长方体框架的长、宽、高是三个连续的自然数,那么搭成的长方体的体积是 120 立方厘米。
【分析】先用棱长总和除以4求出长、宽、高的和,已知长、宽、高是三个连续的自然数,据此求出长、宽、高,再根据长方体的体积公式:v=abh,把数据代入公式解答即可。
【解答】解:长、宽、高的和是:60÷4=15(厘米),
所以长、宽、高分别是6厘米、5厘米、4厘米,
6×5×4=120(立方厘米)
答:搭成的长方体的体积是120立方厘米。
故答案为:120。
31.一个三角形三个内角的度数比是1:1:2,如果其中较短的边长5厘米,则这个三角形的面积是 12.5 平方厘米.
【分析】依据三角形的内角和是180度,利用按比例分配的方法求出角的度数,即可判定三角形的类别,再据三角形的面积公式即可求解.
【解答】解:180°×=90°,
另外两个角的度数相等,即都等于90÷2=45°,
所以这个三角形是等腰直角三角形;
则其两条直角边都等于5厘米,
所以其面积为:5×5÷2,
=25÷2,
=12.5(平方厘米);
答:这个三角形的面积是12.5平方厘米.
故答案为:12.5.
32.(2分)小明家果园里的枇杷树和杨梅树共有480棵,其中杨梅树的棵数是枇杷树的。枇杷树有 400 棵,杨梅树有 80 棵。
【分析】把枇杷树的棵数看作单位“1”,则杨梅的棵数是,两种树的总棵数是(1+),根据分数除法的意义,用480棵除以(1+),就是枇杷树的棵数;再根据分数乘法的意义,用480棵乘(或用两种树的总棵数减枇杷树的棵数),就是杨梅树的棵数。
【解答】解:480÷(1+)
=480÷
=400(棵)
400×=80(棵)
答:枇杷树有400棵,杨梅树有80棵。
故答案为:400,80。
33.(2分)在一幅比例尺是1:3000000的地图上,量得A、B两地的距离是5厘米,A、B两地相距 150 千米。一辆轿车和一辆客车同时从两地相对开出,经过2小时相遇,轿车每小时行驶45千米,则客车每小时行 30 千米。
【分析】已知比例尺和图上距离求实际距离,求出实际距离,再根据:路程÷相遇时间=速度和,速度和﹣甲车速度=乙车速度,解决问题。
【解答】解:5÷=15000000(厘米)
15000000厘米=150千米
150÷2﹣45
=75﹣45
=30(千米/小时);
答:客车每小时行30千米。
故答案为:150,30。
34.(2分)将如图1的正方形进行如下操作:第1次,分别连接对边中点,得到如图2的5个正方形;第2次,将图2左上角正方形按上述方法再分割,得到如图3的9个正方形。依此类推,第4次,同样的操作后会得到 17 个正方形。根据以上操作,若要得到101个正方形,需要操作 25 次。
【分析】第1次得到5个正方形,即4×1+1;
第2次得到9个正方形,即4×2+1;
第3次得到13个正方形,即4×3+1;
……
第n次得到正方形的个数为:4n+1。
【解答】解:4×4+1
=16+1
=17(个)
4n+1=101
4n=100
n=25
答:第4次会得到17个正方形。若要得到101个正方形,需要操作25次。
故答案为:17,25。
五、操作题。(6分)
35.(2分)如图中一个小格的边长表示1千米,A点表示一家餐厅的位置。这家餐厅的送餐广告上说:本餐厅周边3千米的范围内免费送餐。
(1)请在图中表示出这家餐厅的送餐范围。
(2)小明家的位置用数对表示是(7,5),小红家的位置用数对表示是(5,9)。这家餐厅可以给 小明 家免费送餐。(填“小明”或“小红”)
【分析】(1)以点A为圆心,以3格(3千米)为半径画圆,在圆上、圆内的点均为免费送餐的范围。
(2)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可在图中标出小明家、小红家的位置,再看小明家、小红家是在圆外,还是在圆上或圆内。
【解答】解:在图中表示出这家餐厅的送餐范围。
这家餐厅可以给小明家免费送餐。
故答案为:小明。
36.(4分)如图是一个长4厘米、宽2厘米的长方形。
(1)在长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形。
(2)这个梯形的面积是 6 平方厘米。
(3)以等腰直角三角形的一条直角边所在的直线为轴,将三角形旋转一周,可以形成一个 圆锥 。
【分析】(1)要把这个长方形分成一个最大等腰直角三角形和一个梯形,则所画的等腰直角三角形的腰等于长方形的宽,据此画出即可;
(2)通过画图可知,梯形的上底为(4﹣2)厘米,下底为4厘米,高为2厘米,依据梯形的面积=(上底+下底)×高÷2,即可求得梯形的面积。
(3)以等腰直角三角形的一条直角边所在的直线为轴,将三角形旋转一周,可以形成一个圆锥。
【解答】解:(1)如图:
(2)(4﹣2+4)×2÷2
=6×2÷2
=6(平方厘米)
答:这个梯形的面积是6平方厘米。
(3)以等腰直角三角形的一条直角边所在的直线为轴,将三角形旋转一周,可以形成一个圆锥。
故答案为:6平方厘米;圆锥。
六、解决问题。(26分)
37.(4分)只列式或方程,不计算。
(1)王叔叔把20000元年终奖存入银行,定期两年,年利率为2.25%,到期后王叔叔一共可以取回多少元?
(2)眨眼有助于缓解眼睛疲劳,人在正常状态下每分钟眨眼30次,玩手机游戏时眨眼次数比正常状态下减少。玩手机游戏时每分钟眨眼多少次?
【分析】(1)根据本息和=本金+本金×利率×存期,代入数据解答即可。
(2)玩手机游戏时眨眼次数比正常状态下减少,也就是正常状态下的(1﹣),用乘法即可求出玩手机游戏时每分钟眨眼多少次。
【解答】解:(1)20000+20000×2×2.25%
=20000+900
=20900(元)
答:到期后王叔叔一共可以取回20900元。
(2)30×(1﹣)
=30×0.4
=12(次)
答:玩手机游戏时每分钟眨眼12次。
38.(4分)新冠疫情期间,某消毒液生产厂接到一批消毒液订单。工厂生产一周后,已完成与未完成的数量比为2:3,如果再生产18吨,那么正好完成这批订单的一半。这批消毒液订单一共有多少吨?
【分析】已完成与未完成的数量比为2:3,则已经完成了总数的,如果再生产18吨,那么正好完成这批订单的一半,所以18吨占全部的﹣,根据分数除法的意义,用18吨除以其占全部吨数的分率,即得共有多少吨。
【解答】解:18÷(﹣)
=18÷
=180(吨)
答:这批消毒液订单一共有180吨。
39.(4分)根据如图中提供的信息,求小花和小明各看了多少页。(列方程解答)
【分析】根据题意,这道题的等量关系是:小花看的页数﹣小明看的页数=60页,根据这个等量关系,列方程解答。
【解答】解:设小花看了x页。
x﹣x=60
x=100
(页)
答:小花看了100页,小明看了40页。
40.(4分)李师傅要制作一个无盖的圆柱形水桶,用下图所示的长方形铁皮做侧面,要使水桶的容积尽可能大。
(1)应该选用哪张正方形铁皮制作底面?(通过计算说明理由)
(2)这个水桶最多能装水多少升?
【分析】(1)根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,根据圆的周长公式:C=πd,那么d=C÷π,据此求出圆柱的底面直径,然后与四张铁皮进行比较即可解答。
(2)根据圆柱的容积(体积)公式:V=πr2h,把数据代入公式解答。
【解答】解:(1)62.8÷3.14=20(厘米)
所以选择边长是20厘米铁皮作这个水桶的底。
(2)3.14×(62.8÷3.14÷2)2×20
=3.14×20×20
=1256(立方厘米)
1256立方厘米=1.256立方分米
1.256立方分米=1.26升
答:这个水桶最多能装水1.256升。
41.(4分)有64位同学去公园坐船,一共租了12条船,每条大船坐6人,每条小船坐4人,正好坐满。大船和小船各租了多少条?
【分析】假设全部租大船,12条船能坐6×12=72(人),比实际多算了:72﹣64=8(人),因为把小船看作了大船,每条小船多算了6﹣4=2(人),所以小船的条数是(8÷2)条,进而求出大船的条数,据此解答即可。
【解答】解:假设全部租大船,小船的条数为:
(12×6﹣64)÷(6﹣4)
=8÷2
=4(条)
大船的条数为:12﹣4=8(条)
答:大船租8条,小船租4条。
42.(6分)学校环保志愿者对全校师生开展了“垃圾分类、从我做起”的抽样问卷调查,调查结果分析整理后,制作成以下两张统计图。其中丢垃圾行为分为以下几类:
A:能做到垃圾分类投放,并能向周边同学宣传垃圾分类相关知识。
B:能做到垃圾分类投放。
C:能把垃圾放垃圾桶,但不注意分类。
D:存在随手乱丢垃圾的行为。
请根据以上信息,解答下列问题。
(1)学校环保志愿者共调查了多少人?
(2)请将条形统计图补充完整。
(3)如果学校共有师生2200人,则存在随手乱丢垃圾行为的约有多少人?
【分析】(1)把调查的总人数看作单位“1”,能做到垃圾分类投放的有50人,占调查总人数的10%,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(2)根据减法的意义,用减法求出能做到垃圾分类投放,并能向周边同学宣传垃圾分类相关知识的有多少人,据此完成条形统计图。
(3)把该校师生总人数看作单位“1”,存在随手乱丢垃圾的行为的占5%,根据求一个数的百分之几是多少,用乘法解答。
【解答】解:(1)50÷10%
=50÷0.1
=500(人)
答:学校环保志愿者共调查了500人。
(2)500﹣(50+25+25)
=500﹣100
=400(人)
作图如下:
(3)2200×5%=110(人)
答:存在随手乱丢垃圾行为的约有110人。
相关试卷
这是一份2024年江苏省苏州市吴中区小升初模拟数学试卷附答案解析,共16页。
这是一份2024年江苏省苏州市吴中区小升初模拟数学试卷,共17页。试卷主要包含了用心思考,我会填,仔细推敲,我会选,火眼金睛,我会判,细心审题,我能算,心灵手巧,我会画,我会解决问题等内容,欢迎下载使用。
这是一份江苏省苏州市吴中区2023-2024学年一年级上学期期末数学试卷,共8页。试卷主要包含了算一算,填一填,选一选,看图列式,画一画,解决问题等内容,欢迎下载使用。









