2020-2021学年12.2 一次函数备课ppt课件

这是一份2020-2021学年12.2 一次函数备课ppt课件，共23页。PPT课件主要包含了学习目标及重难点，课程导入，ykx，正比例函数，一次函数，课程讲授，新课推进，①列表，②描点，③连线等内容，欢迎下载使用。

1. 掌握一次函数图象的画法并清楚b的含义；(重点)2. 掌握一次函数y=kx+b（k≠0）与y=kx图象的区别与联系.(难点)
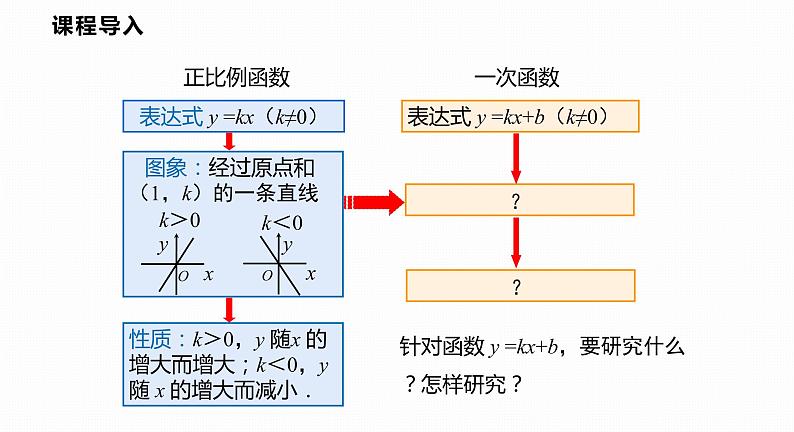
形如 的函数，叫做正比例函数；
形如 的函数，叫做一次函数；
当b=0时，y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数.
正比例函数的图象是一条经过 点的 .
y=kx（k是常数，k≠0）
y=kx+b(k,b是常数，k≠0)
表达式 y =kx（k≠0）
性质：k＞0，y 随x 的增大而增大；k＜0，y 随 x 的增大而减小．
表达式 y =kx+b（k≠0）
针对函数 y =kx+b，要研究什么？怎样研究？
　　研究函数 y =kx+b（k≠0）的图象和性质.　　研究方法：　　画图象→观察图象→变量（坐标）意义解释．
探索1：一次函数的图象的画法
在上一课的学习中，我们学会了正比例函数图象的画法，分为三个步骤．
那么你能用同样的方法画出一次函数的图象吗？
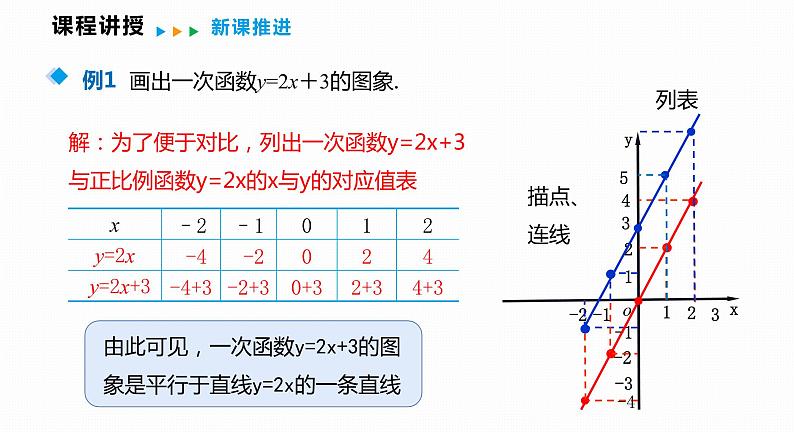
画出一次函数y=2x＋3的图象.
解：为了便于对比，列出一次函数y=2x+3与正比例函数y=2x的x与y的对应值表
一次函数y=kx＋b的图象是一条直线,因此画一次函数图象时,只要确定两个点，再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或( ,0)
与y轴交于点（0，b),b叫做直线 y=kx+b在y轴上的截距．
一次函数y=kx+b的图象是 ，它可由正比例函数y=kx的图象 得到.
直线y=kx+b可以看作是由直线y=kx平移|b|个单位的长度得到（当b>0时,向上平移；当b<0时,向下平移）.
当b＞0时，直线向 平移∣b∣个单位长度；
当b＜0时，直线向 平移∣b∣个单位长度.
在同一坐标系中作出下列函数的图象.
思考：k,b的值跟图象有什么关系？
一次函数y＝kx＋b（k，b为常数，且k≠0）有下列性质： (1)当k＞0时，y随x的增大而增大，这时函数的图象从左到右上升； (2)当k＜0时，y随x的增大而减小，这时函数的图象从左到右下降.
我们把一次函数中k与b的正、负与它的图象经过的象限归纳列表为
2.在平面直角坐标系中，下列直线中与直线y=2x-3平行的是（ ） A.y=x-3 B.y=-2x+3 C.y=2x+3 D.y=3x-2
k 0，b 0
k 0，b 0
k 0，b 0
思考：根据一次函数的图象判断k，b的正负，并说出直线经过的象限：
一次函数y=kx＋b中，k，b的正负对函数图象及性质有什么影响？ 当k＞0时，直线y=kx＋b由左到右逐渐上升，y随x的增大而增大. 当k＜0时，直线y=kx＋b由左到右逐渐下降，y随x的增大而减小.
① b>0时，直线经过 一、二、四象限；
② b<0时，直线经过二、三、四象限.
① b>0时，直线经过一、二、三象限；
② b<0时，直线经过一、三、四象限.
已知一次函数y＝（6＋3m）x＋(m－4)，y随x的增大而增大，函数的图象与y轴的交点在y轴的负半轴上，求m的取值范围.
解： 根据一次函数的特征可知，6＋3m＞0， m－4＜0，解得 －2＜m＜4
1、对于函数y=-2x+1，下列结论正确的是（ ） A.y的值随x值的增大而增大 B.它的图象经过第一、二、三象限 C.它的图象必经过点（-1，2） D.当x＞1时，y＜0
2、已知一次函数y＝mx＋|m＋1|的图象与y轴交于点（0，3），且y随x值的增大而增大，则m的值为（ ). A.2 B.－4 C. －2或－4 D.2或－4
2、下列关系：①面积一定的长方形的长s与宽a； ②圆的周长s与半径a； ③正方形的面积s与边长a； ④速度一定时行驶的路程s与行驶时间a， 其中s是a的正比例函数的有（ ） A.1个 B.2个 C.3个 D.4个
1、已知一次函数y＝mx－(m－2)过原点，则m的值为（ ） A.m＞2 B.m＜2 C.m＝2 D. 不能确定
1、函数y＝kx＋b的图象平行于直线y＝－2x，且与y轴交于点（0，3），则k＝ ，b＝ .
2、已知点A（a＋2，1－a）在函数y＝2x－1的图象上，求a的值.