初中数学沪科版八年级上册15.4 角的平分线备课课件ppt

这是一份初中数学沪科版八年级上册15.4 角的平分线备课课件ppt，共33页。PPT课件主要包含了学习目标及重难点，课程导入，逆命题，课程讲授，新课推进，作射线OP，∴∠AOP∠BOP，应用所具备的条件，应用格式，解如图所示等内容，欢迎下载使用。

1.探索角平分线的逆定理;（重点）2.通过探索角平分线逆定理的过程，体会这个定理的作用，增强几何空间意识.（难点）
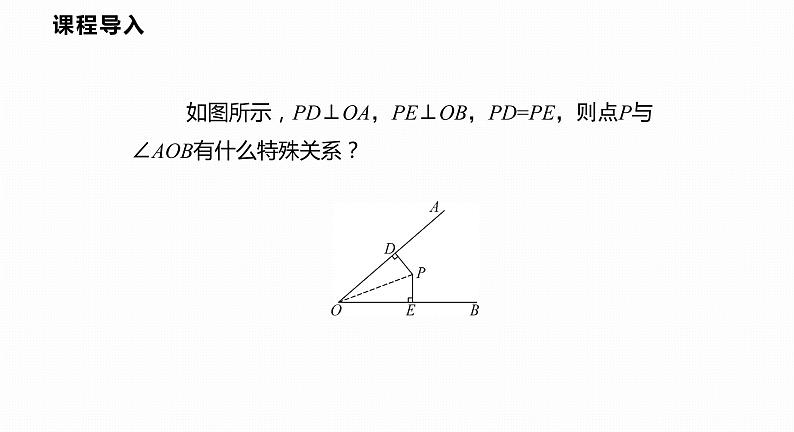
如图所示，PD⊥OA，PE⊥OB，PD=PE，则点P与∠AOB有什么特殊关系？
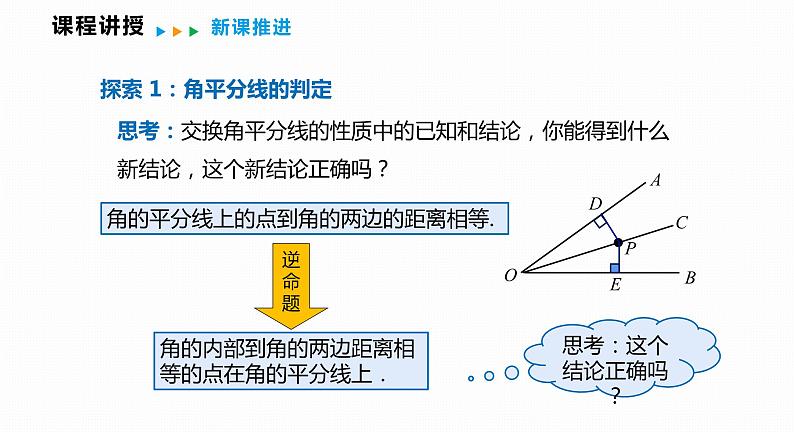
角的内部到角的两边距离相等的点在角的平分线上．
思考：交换角平分线的性质中的已知和结论，你能得到什么新结论，这个新结论正确吗？
角的平分线上的点到角的两边的距离相等.
思考：这个结论正确吗？
探索 1：角平分线的判定
已知：如图，PD⊥OA，PE⊥OB，垂足分别是D、E，PD=PE.求证：点P在∠AOB的角平分线上.
∴点P在∠AOB 角的平分线上.
在Rt△PDO和Rt△PEO 中，
（全等三角形的对应角相等）.
OP=OP（公共边），
PD= PE（已知 ），
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°，
∴Rt△PDO≌Rt△PEO（ HL）.
判定定理： 角的内部到角的两边的距离相等的点在角的平分线上.
定理的作用：判断点是否在角平分线上.
∵ PD⊥OA,PE⊥OB，PD=PE.
∴点P 在∠AOB的平分线上.
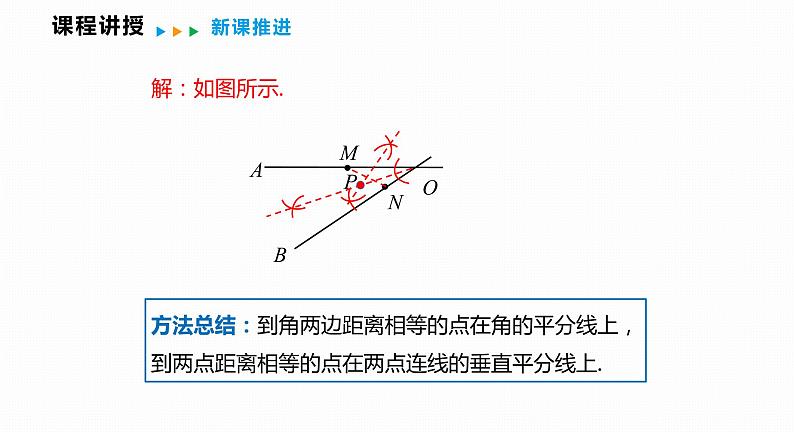
如图，某地有两所大学和两条交叉的公路．图中点M，N表示大学，OA，OB表示公路，现计划修建一座物资仓库，希望仓库到两所大学的距离相同，到两条公路的距离也相同，你能确定出仓库P应该建在什么位置吗？请在图中画出你的设计．(尺规作图，不写作法，保留作图痕迹)
方法总结：到角两边距离相等的点在角的平分线上，到两点距离相等的点在两点连线的垂直平分线上.
活动1 分别画出下列三角形三个内角的平分线，你发现了什么？
发现：三角形的三条角平分线相交于一点
探索 2：三角形的内角平分线
活动2 分别过交点作三角形三边的垂线，用刻度尺量一量，每组垂线段，你发现了什么？
发现：过交点作三角形三边的垂线段相等
已知：如图所示，△ABC中，∠B的平分线BE与∠C的平分线CF相较于点P. 求证：AP平分∠BAC.
证明：过点P分别作PM⊥BC，PN⊥AC，PQ⊥AB，垂足分别为点M,N,Q.
∵ BE是∠B的平分线，点P在BE上，（已知）
∴ PQ=PM（角平分线上的点到角两边的距离相等）
同理， PN=PM.
∴ PN=PQ（等量代换）
∴ AP平分∠BAC.（角的内部到角两边距离相等的点在角的平分线上）
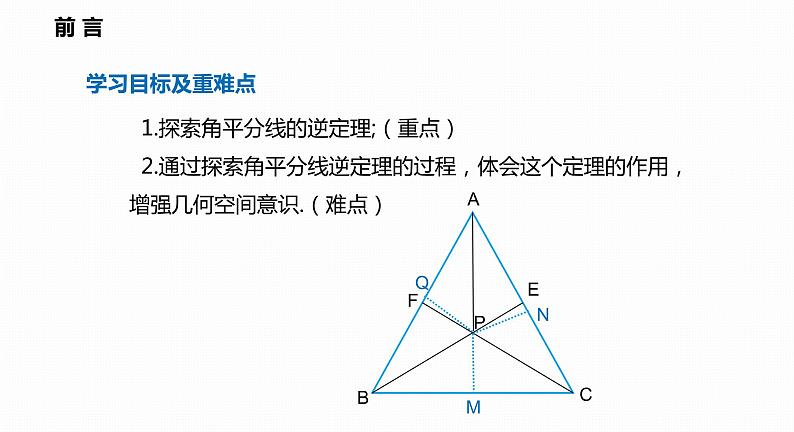
如图，△ABC的角平分线BM，CN相交于点P，求证：点P到三边AB，BC，AC的距离相等.
证明：过点P作PD⊥AB,PE⊥BC,PF⊥AC,垂足分别为D,E,F.∵BM是△ABC的角平分线,点P在BM上,∴PD=PE.同理,PE=PF.∴PD=PE=PF,即点P到三边AB,BC,CA的距离相等.
如图，在直角△ABC中，∠C＝90°，AP平分∠BAC，BD平分∠ABC;AP,BD交于点O，过点O作OM⊥AC,若OM＝4,(1)求点O到△ABC三边的距离和.
方法总结：不存在垂线段———构造应用
(2)若△ABC的周长为32，求△ABC的面积.
1.如图，∠AOP＝∠BOP＝15°，PC∥OA，PD⊥OA，PC＝4，则PD＝(　 　)
A．4　　　　　B．3　　　　　C．2　　　　　D．1
2.到三角形三条边的距离都相等的点是这个三角形的(　 　)A．三条中线的交点　　　　　　　B．三条高的交点C．三条边的垂直平分线的交点 D．三条角平分线的交点
3.如图所示，已知BE⊥AC于E，CF⊥AB于F，BE、CF相交于点D，若BD＝CD.求证：AD平分∠BAC.
证明：∵BE⊥AC，CF⊥AB，∴∠BFD＝∠CED＝90°.又∵∠BDF＝∠CDE，BD＝CD，∴△BDF≌△CDE(AAS)，∴DF＝DE，∴点D在∠BAC平分线上，AD平分∠BAC.
如图，要在S区建一个贸易市场，使它到铁路和公路距离相等， 离公路与铁路交叉处500米，这个集贸市场应建在图上何处？（比例尺为1︰20000）
0.025m＝2.5cm
在角平分线上截取OD=2.5cm，则D点即为所求点.
解：作夹角的角平分线OC，设集贸市场距交点O为 x m，根据题意得
如图所示，OC平分∠AOB，P为OC上一点，PD⊥OA于点D，E为OA上一点，∠PEO+∠PFO=180°.求证：OE+OF=2OD.
又∵∠PEO+∠PFO=180°，（已知）∠PFM+∠PFO=180°，（平角定义）∴∠PED=∠PFM.又∵PD⊥OA，PM⊥OB，（已知）∴∠PDE=∠PMF=90°.（垂直定义）
如图所示，CD⊥AB，BE⊥AC，垂足分别为点D，E，BE，CD相交于点O，且OB=OC.求证：点O在∠BAC的平分线上.
证明：∵CD⊥AB，BE⊥AC，∴∠BDO=∠CEO=90°.又∵OB=OC，（已知）∠BOD=∠COE，（对顶角相等）∴△BOD≌△COE（AAS）∴OD=OE.
∴点O在∠BAC的平分线上.（角的内部到角两边距离相等的点在角的平分线上）
如图，已知∠CBD和∠BCE的平分线相交于点F，求证：点F在∠DAE的平分线上．
过点F作FG⊥AE于G，FH⊥AD于H，FM⊥BC于M.
∵点F在∠BCE的平分线上， 　　　　FG⊥AE， FM⊥BC.
又∵点F在∠CBD的平分线上， 　　　　FH⊥AD， FM⊥BC，
∴点F在∠DAE的平分线上.　　　
如图, D, E, F分别是△ABC三边上的点, CE=BF, △DCE和△DBF的面积相等, DH⊥AB于H, DG⊥AC于G. 求证: AD平分∠BAC.
又∵ △DCE和△DBF的面积相等，且CE=BF
又∵ DH⊥AB，DG⊥AC
如图，O是三条角平分线的交点，OD⊥BC于D，若OD=3， △ABC的周长为15，求S△ABC .
证明：过点O分别作OE⊥AB，DF⊥AC，
垂足分别为E，F，连接AO.
∵ OB，OC分别平分∠ABC和∠ACB，且OD⊥BC
S△ABO+S△BOC+S△AOC
×(AB+BC+AC)
又∵ OD=3， △ABC的周长为15.
如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置.