2022版高考数学二轮复习 第2篇 专题1 三角函数、三角恒等变换与解三角形 第2讲课件

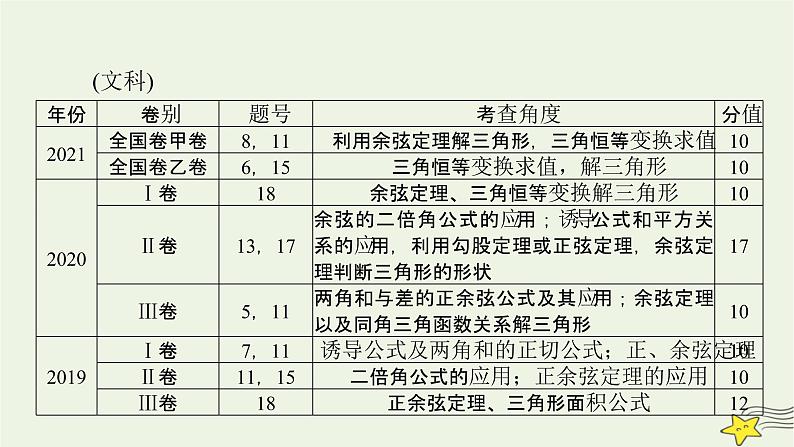
这是一份2022版高考数学二轮复习 第2篇 专题1 三角函数、三角恒等变换与解三角形 第2讲课件，共60页。PPT课件主要包含了高频考点，真题热身，感悟高考，考点二解三角形，典例1，典例2等内容，欢迎下载使用。
专题一　三角函数、三角恒等变换与解三角形
第二讲　三角恒等变换与解三角形
导航立前沿•考点启方向
自主先热身•真题定乾坤
核心拔头筹•考点巧突破
明晰易错点•高考零失误
1．利用各种三角函数进行求值与化简，其中降幂公式、辅助角公式是考查的重点．2．利用正、余弦定理进行边和角、面积的计算，三角形形状的判定以及有关范围的计算，常与三角恒等变换综合考查．
7．(2020·全国卷Ⅱ卷)△ABC中，sin2A-sin2B-sin2C＝sin Bsin C.(1)求A；(2)若BC＝3，求△ABC周长的最大值．
1．高考对此部分的考查一般以“二小”或“一大”的命题形式出现．2．若无解答题，一般在选择题或填空题各有一题，主要考查三角恒等变换、解三角形，难度一般，一般出现在第4～9或第13～15题位置上．3．若以解答题命题形式出现，主要考查三角函数与解三角形的综合问题，一般出现在解答题第17题位置上，难度中等．
考点一　三角恒等变换与求值
(1)三角恒等变换的三原则①一看“角”，这是最重要的一环，通过看角之间的差别与联系，把角进行合理拆分，从而正确使用公式，如2题．②二看“函数名称”，看函数名称之间的差异，从而确定使用的公式，常见的有“切化弦”．③三看“结构特征”，分析结构特征，可以帮助我们找到变形的方向，常见的有“遇到分式要通分”等．
(2)解决条件求值应关注的三点①分析已知角和未知角之间的关系，正确地用已知角来表示未知角．②正确地运用有关公式将所求角的三角函数值用已知角的三角函数值来表示．③求解三角函数中给值求角的问题时，要根据已知求这个角的某种三角函数值，然后结合角的取值范围，求出角的大小，如7题．
角度1　利用正弦、余弦定理判断三角形的形状在△ABC中，a，b，c分别表示三个内角A，B，C的对边，如果(a2＋b2)sin(A-B)＝(a2-b2)·sin(A＋B)，则△ABC的形状为(　　)A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰三角形或直角三角形
【解析】　解法一：已知等式可化为a2[sin(A-B)-sin(A＋B)]＝b2[-sin(A＋B)-sin(A-B)]，∴2a2cs Asin B＝2b2cs Bsin A．由正弦定理，上式可化为sin2Acs Asin B＝sin2Bcs Bsin A，∴sin Asin B(sin Acs A-sin Bcs B)＝0，∵A，B均为△ABC的内角，∴sin A≠0，sin B≠0，∴sin 2A-sin 2B＝0，即sin 2A＝sin 2B.
6．如图，在△ABC中，内角A，B，C的对边分别为a，b，c，已知c＝4，b＝2，2ccs C＝b，D，E分别为线段BC上的点，且BD＝CD，∠BAE＝∠CAE.(1)求线段AD的长；(2)求△ADE的面积．
1．仰角和俯角在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下方的角叫俯角(如图①)．
考点三　正、余弦定理的实际应用
2．方位角从指北方向顺时针转到目标方向线的水平角，如B点的方位角为α(如图②)．3．方向角相对于某一正方向的水平角．(1)北偏东α，即由指北方向顺时针旋转α到达目标方向(如图③)．(2)北偏西α，即由指北方向逆时针旋转α到达目标方向．(3)南偏西等其他方向角类似．
4．坡角与坡度(1)坡角：坡面与水平面所成的二面角的度数(如图④，角θ为坡角)．(2)坡度：坡面的铅直高度与水平长度之比(如图④，i为坡度)．坡度又称为坡比．
2．(2021·北京高三模拟)魏晋南北朝(公元220-581)时期，中国数学在测量学取得了长足进展．刘徽提出重差术，应用中国传统的出入相补原理，通过多次观测，测量山高水深等数值，进而使中国的测量学达到登峰造极的地步，超越西方约一千年，关于重差术的注文在唐代成书，因其第一题为测量海岛的高度和距离(图1)，故题为《海岛算经》受此题启发，小清同学依照此法测量奥林匹克公园奥林匹克塔的高度和距离(示意图如图2所示)，录得以下是数据(单位：米)：前表却行DG＝1，表高CD＝EF＝2，后表却行FH＝3，表间DF＝244.则塔高AB＝__________米，前表去塔远近BD＝__________米．
3．如图所示，在一个坡度一定的山坡AC的顶上有一高度为25 m的建筑物CD，为了测量该山坡相对于水平地面的坡角θ，在山坡的A处测得∠DAC＝15°，沿山坡前进50 m到达B处，又测得∠DBC＝45°，根据以上数据可得cs θ＝__________.
解三角形实际问题的4步骤
易错点一：三角恒等变换时求错角的范围
【易错释疑】　上述错误的解法是在利用同角三角函数忽略了α＋2β的范围，导致求错了cs(α＋2β)的值，故导致后面计算sin(α＋β)时尽管利用对了公式，但是结果也是错误的，所以在三角恒等变换求值时，如果角给了范围，一定要求对角的范围，范围越准确越好．
(2021·佛山模拟)在△ABC中，角A，B，C的对边分别为a，b，c，且a＜b＜c，现有三个条件：①a、b、c为连续偶数；②sin B＝2sin A；③sin2A＋sin2B＋cs2C＝1(1)从上述三个条件中选出________两个，使得△ABC不存在，并说明理由；(2)从上述三个条件中选出________两个，使得△ABC存在；若△ABC存在且唯一，请求出a的值；若△ABC存在且不唯一，请说明理由．
易错点二：解三角形时忽视对三角形的解的个数的讨论
【解析】　(1)选①②时，△ABC不存在，理由如下：因为a、b、c为连续偶数，且a＜b＜c，所以b＝a＋2，又由②sin B＝2sin A及正弦定理可得b＝2a，所以2a＝a＋2，此时a＝2，b＝4，c＝6，不满足a＋b＞c，故△ABC不存在．
(2)选①③时，△ABC存在且唯一，理由如下：因为a、b、c为连续偶数，且a＜b＜c，所以b＝a＋2，c＝a＋4，由③sin2A＋sin2B＋cs2C＝1，可得sin2A＋sin2B＝sin2C，再由正弦定理可得a2＋b2＝c2，所以a2＋(a＋2)2＝(a＋4)2，解得a＝6，(负值舍去)，此时a＝6，b＝8，c＝10，故△ABC存在且唯一，
【易错释疑】　(1)求解此类题时避免出错的关键：一是会选定理，即根据已知的边角关系，恰当地选用正弦定理或余弦定理解三角形，一般地，知两边和其中一边所对的角(既要注意角和边的对应，还要注意讨论钝角与锐角)或一边和两角，常利用正弦定理解三角形，知三边或两边与其夹角，常利用余弦定理解三角形；二是会用公式，即会利用二倍角公式、两角和与差的正弦和余弦公式求三角函数值．
(2)在△ABC中，已知a，b和A，三角形的解的个数的情况如下，①A为锐角时，当0