2022年中考数学总复习课件合集

这是一份2022年中考数学总复习课件合集，共60页。PPT课件主要包含了知识清单·主干回顾，b＋a，a＋b＋c，abc，ab＋ac，云南5年真题，高频考点·疑难突破，第三讲分式，第四讲二次根式，a≥0等内容，欢迎下载使用。
一、有理数的有关概念1．数轴：规定了原点、正方向、_________的直线．2．相反数：a的相反数是____．互为相反数的两个数的和是__．3．倒数：乘积为__的两个数互为倒数，a(a≠0)的倒数是__，__没有倒数．4．绝对值：(1)从“数”的角度看：(2)从“形”的角度看：一个数的绝对值就是表示这个数的点到_____的距离．二、科学记数法科学记数法的一般形式：把一个数写成______的形式(其中__≤ ＜___，n为整数).
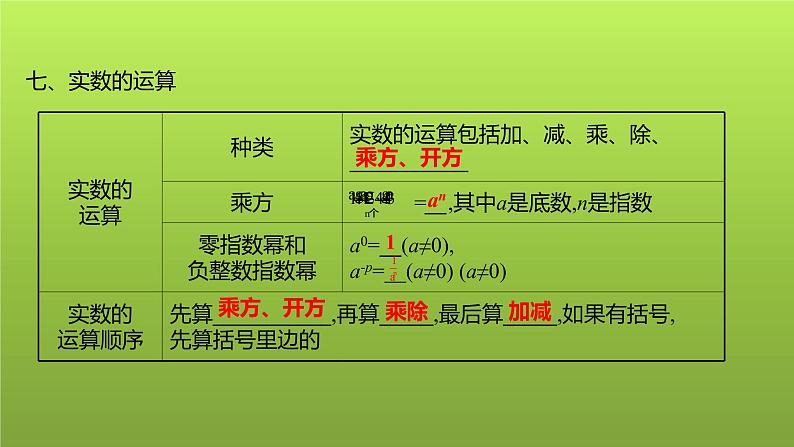
三、有理数的运算律(用字母表示)1．加法交换律：a＋b＝_____．2．加法结合律：(a＋b)＋c＝_________．3．乘法交换律：ab＝___．4．乘法结合律：(ab)c＝_____．5．乘法分配律：a(b＋c)＝______．四、实数的有关概念及分类
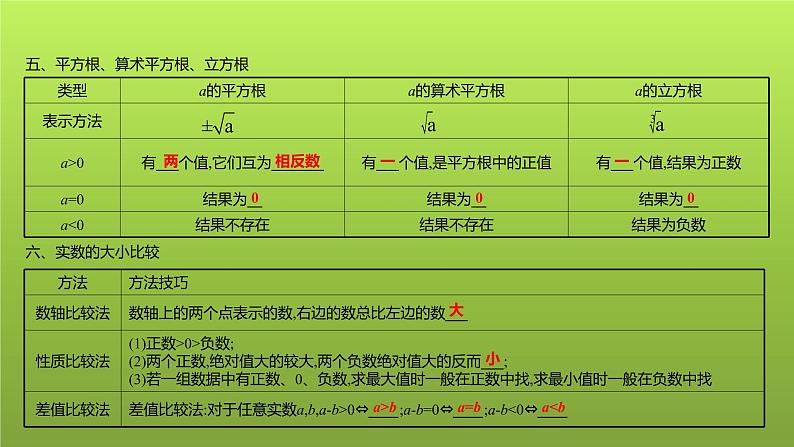
五、平方根、算术平方根、立方根六、实数的大小比较
第二讲　整式、因式分解
一、代数式1．用基本的运算符号(基本运算包括加、减、乘、除、乘方和开方)把___或表示数的_____连接起来的式子，叫做代数式．2．列代数式：把问题中与数量有关的词语，用含有数、字母和运算符号的式子表示出来．关键是找出问题中的数量关系及公式，如路程＝速度×时间，售价＝标价×折扣等；其次要抓住一些关键词语，如：多、少、大、小、增长、下降等．3．求代数式的值(1)直接代入法：把已知字母的值代入代数式，并按原来的运算顺序计算求值．(2)整体代入法：利用提公因式法、平方差公式、完全平方公式和降次等方法对所求代数式、已知等式进行恒等变形，使所求代数式变形成含有已知整式或部分项的形式，若涉及相反数、倒数需转化为两数和的形式或积的形式，再整体代入求值．
二、整式的有关概念2．同类项：所含字母_____，且相同字母指数也_____的单项式．
am+an+bm+bn
四、因式分解1．定义：把一个多项式化成几个整式的___的形式，这种变形叫做多项式的因式分解．2．方法：(1)提公因式法：am＋bm＋cm＝__________．
4x(xy＋1)(xy－1)
一、分式的概念和基本性质1．分式的概念：一般地，如果A，B表示两个_____，并且B中含有_____，那么式子 叫做分式．2．分式有意义的条件：分母______．3．分式的值为0的条件：分子____，但分母______．4．分式的基本性质：分式的分子与分母同乘(或除以)同一个不等于0的_____，分式的值_____．用式子表示： ＝_____＝ _____(其中M为不等于0 的整式).
一、二次根式的相关概念1．二次根式：形如____(____)的代数式．2．二次根式的性质：(1) (a≥0)是 _____数；(2) (a≥0)＝__；(3)( )2＝__(a≥0).二、二次根式的运算1．最简二次根式：最简二次根式要同时具备下列两个条件：(1)被开方数不含_____；(2)被开方数中不含___________的因数或因式．
(1)(2)(5)(6)(7)(8)(10)(11)(12)(13)
第五讲　一次方程(组)
一、等式的性质等式的性质1：如果a＝b，那么a±c＝____；等式的性质2：如果a＝b，那么ac＝__；如果a＝b，那么 ＝____(c≠0).二、一元一次方程及其解法1．定义：含有_____未知数，且未知数的________，等号两边都是_____的方程．2．一元一次方程的解：能使一元一次方程左右两边_____的未知数的值．3．解一元一次方程的步骤：去分母、_______、_____、___________、系数化为1.三、二元一次方程组及其解法1．定义：含有___个未知数，并且含有___________的次数都是1的_____方程叫做二元一次方程．把具有相同未知数的两个二元一次方程合在一起叫做二元一次方程组．2．二元一次方程组的解：能够使方程组的每个方程都成立的未知数的值．3．解二元一次方程组的思想：_____．4．解法：(1)_____消元法．(2)_____消元法．
四、列方程(组)解应用题常见的等量关系1．工程问题：工作量＝工作时间×_________．2．利润问题：(1)商品的利润＝售价－_____．(2)商品的售价＝________________×折数．(3)商品的利润率＝_________÷商品进价＝(商品售价－进价)÷商品进价．3．行程问题：(1)往返路程相等，即顺流(风)速度__顺流(风)时间＝逆流(风)速度__逆流(风)时间．(2)轮船(飞机)本身速度不变，即顺流(风)速度___水(风)速度＝逆流(风)速度＋水(风)速度．
一、分式方程的定义分母里含有_______的方程叫做分式方程．二、分式方程的解法解分式方程的基本思路是_________________________，具体步骤是：①去分母，在方程的两边都乘以___________，约去分母，化成整式方程；②解这个整式方程；③验根，把整式方程的根代入___________，看结果是不是零，使最简公分母为零的根是原方程的增根，必须舍去．
将分式方程转化为整式方程
三、分式方程的增根分式方程增根的两个特征：(1)增根使___________为0.(2)增根是分式方程化成的_________的根．四、列分式方程解应用题列分式方程解应用题的关键是分析题意、找准等量关系、设出未知数、列出方程，最后还要注意求出的未知数的值不但要是所列方程的根，而且还要符合实际意义．
一、一元二次方程的概念1．定义：只含有1个未知数，并且未知数的最高次数是2的整式方程．2．一般形式：__________________．二、一元二次方程的解法
ax2＋bx＋c＝0(a≠0)
三、根的判别式与一元二次方程的根的情况1．Δ＝b2－4ac＞0⇔方程_____________的实数根．2．Δ＝b2－4ac＝0⇔方程___________的实数根．3．Δ＝b2－4ac＜0⇔方程_____实数根．四、根与系数的关系　如果方程ax2＋bx＋c＝0(a≠0)的两个实数根是x1，x2，那么x1＋x2＝_______，x1·x2＝________．
　问题3　若关于x的一元二次方程(k－3)x2－3x＋2＝0的一个根为2，则k的值为__．【提分要点】若已知方程的一根，求代数式或待定系数的值时，则可根据一元二次方程的根的定义，把根代入原方程，得到一个关于某个字母的方程，通过方程求代数式的值或解方程求字母的值．问题4　若关于x的一元二次方程(k－3)x2－3x＋2＝0有实数根，求k的取值范围．
第八讲　一元一次不等式(组)
一、不等式的性质1．性质1：不等式两边加(或减)同一个数(或式子)，不等号的方向_____．即如果a>b，那么a±c___b±c.2．性质2：不等式两边乘(或除以)同一个正数，不等号的方向_____．即如果a>b，c>0，那么ac___bc(或 ___ ).3．性质3：不等式两边乘(或除以)同一个负数，不等号的方向_____.即如果a>b，c(m－2)x＋m＋4的解集为_____．问题13　若该一次函数的图象与坐标轴只有一个交点，过点A(－2，4)的直线 l2与该一次函数图象交于点B(－1，b)，求直线l2的解析式．
第十一讲　一次函数的应用
一、列一次函数解应用题　列一次函数解应用题与列整式方程解应用题的思路和方法是一致的，不同的是，学习了一次函数后，表示量与量的关系的代数式是含有两个变量的等式．对于应用题要注意以下步骤：(1)审清题意，弄清题中涉及哪些量，已知量有几个，已知量与变量之间的基本关系是什么，找出等量关系(即函数关系).(2)设出两个变量，注意分清自变量和因变量，同时还要注意所设变量的单位要准确．
(3)列函数解析式，抓住题中含有等量关系的语句，将此语句抽象为含变量的等式，这就是一次函数．(4)按题目要求，结合一次函数的性质解答相应的问题．(5)检验所得解是否符合实际，即是否为所提问题的答案．(6)写出答案．
二、建立一次函数模型求解实际问题1．一般步骤：(1)恰当地建立直角坐标系．(2)将已知条件转化为点的坐标．(3)合理地设出所求函数解析式．(4)代入已知条件或点的坐标，求出解析式．(5)利用解析式求解问题．2．利用一次函数解决实际问题，要建立数学模型，即把实际问题转化为一次函数问题，利用题中存在的公式、内含的规律等相等关系，建立函数解析式，再利用函数的图象及性质去研究问题．
【自我诊断】(打“√”或“×”)1．如图所示，购买一种苹果，所付款金额y(元)与购买量x(kg)之间的函数图象由线段OA和射线AB组成，则一次购买3 kg这种苹果比分三次每次购买1 kg这种苹果可节省2元．( )
2．如图(1)，在某个盛水容器内，有一个小水杯，小水杯内有部分水，现在匀速持续地向小水杯内注水，注满小水杯后，继续注水，小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图(2)中的图象，则至少需要5 s能把小水杯注满．( )
一、反比例函数解析式的三种形式1．y＝___(k≠0，k为常数).2．y＝k ___(k≠0，k为常数).3．xy＝__(k≠0，k为常数).二、反比例函数的图象与性质1．反比例函数y＝ (k为常数，k≠0)的图象是_______，且关于_____对称．2．反比例函数y＝ (k为常数，k≠0)的图象和性质．
第十三讲　二次函数的图象与性质
一、二次函数的概念及其关系式1．二次函数的概念：形如_____________(a，b，c是常数，a≠0)的函数．2．二次函数的解析式：(1)一般式：__________________．(2)顶点式：y＝a(x－h)2＋k(a≠0)，其顶点坐标是______.(3)交点式：y＝a(x－x1)(x－x2)(a≠0)，其图象与x轴的交点坐标为(x1，0)，(x2，0).
y＝ax2＋bx＋c(a≠0)
【自我诊断】(打“√”或“×”)1．二次函数y＝x2＋4x－5的图象的对称轴为x＝2.( )2．将y＝－2x2＋1向右平移1个单位，再向上平移2个单位后，所得的抛物线是y＝－2(x－1)2＋3.( )3．若二次函数y＝x2＋bx的图象的对称轴是经过点(2，0)且平行于y轴的直线，则关于x的方程x2＋bx＝5的解为x1＝－1，x2＝5.( )
第十四讲　二次函数的应用
二、利用二次函数解决实际问题的步骤(1)根据题意，写出二次函数的_______．(2)考虑自变量的_________．(3)根据二次函数的性质，结合自变量的_________，给出实际问题的答案．
【自我诊断】(打“√”或“×”)　某服装店购进单价为15元童装若干件，销售一段时间后发现：当销售价为25元时平均每天能售出8件，而当销售价每降低2元，平均每天能多售出4件，当每件的定价为22元时，该服装店平均每天的销售利润最大．( )
第十五讲　图形初步知识
一、线和角1．两个基本事实：(1)经过两点有且只有_____直线．(2)两点之间，_____最短．2．互余的性质：同角(或等角)的余角_____．3．互补的性质：同角(或等角)的补角_____．4．对顶角的性质：对顶角_____．二、垂直及其性质1．点到直线的距离：直线外一点到这条直线的_______的长度．2．垂直的基本性质：(1)在同一平面内，过一点_________一条直线垂直于已知直线．(2)连接直线外一点与直线上各点的线段中，_______最短．
三、平行线的性质及判定
一、三角形中的三条重要线段1．中线：三角形的三条中线的交点在三角形的___部，这个交点叫做三角形的_____．2．角平分线：三角形的三条角平分线的交点在三角形的___部．3．高：_____三角形的三条高的交点在三角形的内部；直角三角形的三条高的交点是_________；_____三角形的三条高所在直线的交点在三角形的外部．二、三角形的三边关系三角形的两边之和_____第三边，三角形的两边之差_____第三边．
三、三角形的内角和定理及推论1．定理：三角形三个内角的和等于____．2．推论：(1)三角形的一个外角等于和它_________________的和．(2)直角三角形的两个锐角_____．四、多边形1．内角和定理：n边形的内角和是___________．2．外角和定理：任意多边形的外角和为____．3．正多边形：各个角_____，各条边_____的多边形．
一、概念：能够_________的两个三角形．二、性质：全等三角形的对应边_____，对应角_____．三、判定定理1．三边分别_____的两个三角形全等(简写成“边边边”或“____”).2．两边和它们的夹角分别_____的两个三角形全等(简写成“边角边”或“____”).3．两角和它们的夹边分别_____的两个三角形全等(简写成“角边角”或“_____”).4．两角和其中一个角的对边分别_____的两个三角形全等(简写成“角角边”或“_____”).
5．斜边和一条直角边分别_____的两个直角三角形全等(简写成“斜边、直角边”或“___”).四、角平分线的性质与判定1．性质：角平分线上的点到角两边的_____相等．2．判定：角的内部到角的两边的距离相等的点在这个角的_______上．五、线段的垂直平分线1．性质：线段垂直平分线上的点与这条线段两个端点的距离_____.2．判定：与一条线段两个端点距离相等的点，在这条线段的___________上．
第十八讲　等腰三角形和直角三角形
底边上的中线(或底边上的高或
顶角平分线)所在的直线
三、直角三角形的性质与判定
四、勾股定理及逆定理1．勾股定理：如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么_________．2．勾股定理的逆定理：如果三角形的三边长a，b，c满足_________，那么这个三角形是直角三角形．五、命题、定理1．互逆命题：如果两个命题的_____和_____正好相反，我们把这样的两个命题叫做互逆命题，如果把其中一个叫做原命题，那么另一个叫做它的_______．2．互逆定理：若一个定理的逆命题是正确的，那么它就是这个定理的逆定理，称这两个定理为_____定理．
　问题1　若BD为AC边上的中线，且BD＝6.则∠ABD___∠CBD (填“＞”“＜”或“＝”)，BD与AC的位置关系为_____，△ABC的面积＝______．
第十九讲　解直角三角形
一、特殊角的三角函数值
二、直角三角形中的边角关系1．三边之间的关系：_________．2．两锐角之间的关系：_____________．3．边角之间的关系：sin A＝cs B＝____，sin B＝cs A＝ ____ ，tan A＝ ____ ，tan B＝ ____ ．三、解直角三角形的应用1．仰角和俯角：如图1，在同一铅垂面内视线和水平线间的夹角，视线在水平线_____的叫做仰角，在水平线_____的叫做俯角．
2．坡度(坡比)和坡角：如图2，通常把坡面的铅直高度h和_________之比叫做坡度(或叫做坡比)，用字母_表示，即i＝___；坡面与_______的夹角叫做坡角，记作α.所以i＝___＝tan α.3．方位角：指北或指南的方向线与目标方向所成的_______的角叫做方位角．
一、平行四边形1．概念：两组对边分别_____的四边形．2．性质与判定：
二、三角形的中位线1．定义：连接三角形两边_____的线段叫做三角形的中位线．2．性质：三角形的中位线_____于三角形的第三边，且等于第三边的_____．
　问题1　若AB∥CD，请添加一个条件_________________________________________________________________________________________________________(写出一个即可)，使四边形ABCD是平行四边形．
AD∥BC(或∠ADC＋∠BCD＝180°或
∠DAB＋∠ABC＝180°或∠DAC＝∠ACB或∠ADB＝∠DBC或AB＝CD等，答案不
　问题2　若∠ABC＝∠ADC，请添加一个条件______________，使四边形ABCD是平行四边形，判定依据是________________________________________________．　问题3　若AD＝BC，请添加一个条件________(写出一个即可)，使四边形ABCD是平行四边形，判定依据是_________________________________________________．　问题4　若AO＝OC，请添加一个条件________(写出一个即可)，使四边形ABCD是平行四边形，判定依据是______________________________________________．
两组对角分别相等的四边形是平行四边形(答案不
的四边形是平行四边形(答案不唯一)
对角线互相平分的四边形是平行四边形(答
　问题5　若四边形ABCD是平行四边形，下列结论中不一定正确的是(　　)A．AB＝CD　　　　　　B．BO＝ODC．∠BAD＝∠BCD D．AB⊥AC　问题6　若四边形ABCD是平行四边形，且AB＝10，AD＝6，则OA的取值范围是_________．　【提分要点】解决此类问题的关键是根据三角形的三边关系确定对角线的取值范围，然后利用对角线相互平分即可解决．
　问题8　如图所示，若四边形ABCD为平行四边形，AB＝10，若点E为BC的中点，连接OE，则OE＝__． 　问题9　如图所示，若四边形ABCD为平行四边形，AE是∠BAD的平分线，∠AEB＝65°，则∠BCD＝____．　问题10　若四边形ABCD为平行四边形，AB＝4，AC＝6，BD＝10，则▱ABCD的面积为___.
第二十一讲　矩形、菱形、正方形
矩形、菱形、正方形的性质和判定
∠BAD＝90°或∠ABC＝90°或∠BCD＝90°或∠ADC＝90°或AC＝BD
AB＝BC或AB＝AD或BC＝CD或AD＝CD或AC⊥BD(写出一个即可)
一、圆的定义及圆的轴对称性1．定义：在一个平面内，线段OA绕它固定的一个端点O旋转_____，另一个端点A所形成的图形．2．轴对称性：圆是___________，任何一条_____________都是它的对称轴．二、垂径定理及推论1．垂径定理：垂直于弦的直径_______，并且平分弦所对的_______.2．推论：平分弦(不是直径)的直径_________，并且平分弦所对的_______．三、弧、弦、圆心角之间的关系1．定理：在同圆或等圆中，相等的圆心角所对的弧_____，所对的弦也_____．2．推论：(1)在同圆或等圆中，如果两条弧相等，那么它所对的圆心角_______，所对的弦也_____．(2)在同圆或等圆中，如果两条弦相等，那么它所对圆心角_____，所对的弧也_____．
四、圆周角定理及推论1．定理：在同圆或等圆中，同弧或等弧所对的圆周角_____，都等于这条弧所对的圆心角的_____．2．推论：(1)半圆(或直径)所对的圆周角是_____，90°的圆周角所对的弦是_____．(2)在同圆或等圆中，如果两个圆周角_____，它们所对的弧一定_____．五、圆内接四边形的性质1．圆内接四边形的对角_____．2．圆内接四边形的任意一个角的外角等于它的内对角．
第二十三讲　与圆有关的位置关系
一、点与圆的位置关系1．设圆O的半径为r，点P到圆心的距离为OP＝d.则：点P在圆外⇔____；点P在圆上⇔____；点P在圆内⇔____．2．确定圆的条件：不在同一直线上的三个点确定_____圆．3．三角形的外心：三角形外接圆的圆心，是三角形三边的___________的交点．二、直线与圆的位置关系1．三种位置关系：_____、_____、_____．2．切线的定义、性质与判定：(1)定义：和圆有_____公共点的直线．(2)性质：圆的切线_______过切点的直径．(3)判定：经过半径的外端，并且_____于这条半径的直线是圆的切线．3．切线长定理：从圆外一点可以引圆的两条切线，它们的切线长_____，这一点和圆心的连线_____两条切线的夹角．三、三角形的内切圆1．定义：与三角形各边都_____的圆．2．三角形的内心：三角形_______的圆心，是三角形三条_________的交点．
第二十四讲　圆的有关计算
一、正多边形和圆1．定义：各边_____，各角也都_____的多边形是正多边形．2．正多边形和圆的关系：把一个圆______，依次连接_______可作出圆的内接正n边形．二、圆中的弧长与扇形面积1．半径为R的圆中，n°的圆心角所对的弧长l的计算公式为l＝________．2．扇形面积：(1)半径为R的圆中，圆心角为n°的扇形面积为S扇形＝ ________ ．(2)半径为R，弧长为l的扇形面积为S扇形＝______．三、圆锥的侧面积、全面积计算公式设圆锥的母线长为l，底面半径为R，则有：S侧面积＝____，S全面积＝_________．
第二十五讲　平移、旋转与轴对称
1．平移的性质：(1)平移后的图形与原图形的对应线段_____(或在同一条直线上)且_____，对应角_____．(2)连接各组对应点的线段_____(或在同一条直线上)且_____.2．旋转的性质：(1)对应点到旋转中心的距离_____．(2)对应点与旋转中心所连线段的夹角等于_______．(3)旋转前、后的图形_____．3．轴对称的性质：(1)如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的___________．(2)轴对称图形的对称轴是任何一对对应点所连线段的___________．4．中心对称的性质：(1)中心对称的两个图形，对称点所连线段都经过_________，而且被对称中心所_____．(2)中心对称的两个图形是_____图形．
一、相似三角形的性质性质1：相似三角形的对应角_____，对应边的比 _____．性质2：相似三角形周长的比等于_______．性质3：相似三角形对应高的比、对应中线的比、对应角平分线的比等于_______．性质4：相似三角形的面积的比等于相似比的_____．二、相似三角形的判定判定1：平行于三角形一边的直线和其他两边(或两边的延长线)相交，所构成的三角形与原_______相似(相似三角形的预备定理).判定2：三边_______的两个三角形相似．判定3：两边_______且_________的两个三角形相似．判定4：两角_________的两个三角形相似．
三、位似1．两个特点：(1)是_____图形．(2)对应顶点的连线交于_____．2．坐标系中两个位似图形对应点的坐标关系：以原点为位似中心，相似比为k的两个位似图形，原图形上某点坐标为(x，y)，则新图形上对应点的坐标为________或____________.
第二十七讲　投影与视图
3．三视图的画法：(1)主视图的长与俯视图的长对正，主视图的高与左视图的高平齐，俯视图的宽与左视图的宽相等；(2)画三视图时，看得见的轮廓线用_____，看不见的轮廓线应画成_____．
4．常见立体图形的视图
【自我诊断】(打“√”或“×”)　如图，位似图形由三角尺与其灯光照射下的中心投影组成，相似比为2∶5，且三角尺的一边长为8 cm，则投影三角尺的对应边长为10 cm.( )
第二十八讲　数据的收集、整理与描述
一、数据的收集1．收集方式：(1)全面调查：考察_____对象的调查．(2)抽样调查：只抽取_______对象进行调查，然后根据调查数据推断全体对象的情况．2．相关概念：(1)总体：所要考察的_____对象．(2)个体：组成总体的_______考察对象．(3)样本：被抽取的那些_____组成一个样本．(4)样本容量：样本中_____的数目．
二、数据的整理1．概念：(1)频数：在统计数据中落在不同小组中_____的个数．(2)频率：某个组的频数与_________的比值，叫做这个组的频率．2．方法：一般采用_____法统计数据出现的频数，然后画频数分布直方图．
【自我诊断】(打“√”或“×”)1．在一次数学测试中，某班50名学生的成绩分为六组，第一组到第四组的频数分别为6，8，9，12，第五组的频率是0.2，则第六组的频数是10.( )2．为了解学生课外阅读的喜好，某校从八年级1 200名学生中随机抽取50名学生进行问卷调查，整理数据后绘制如图所示的统计图．由此可估计该年级喜爱“科普常识”的学生约有360人．( )
3．下面的折线图描述了某地某日的气温变化情况，根据图中信息知气温是30 ℃的时刻为16：00.( )
本校500名学生每月的零花钱数额
20名学生每月的零花钱数额
第二十九讲　数据的分析
2．中位数：将一组数据按照从小到大(或从大到小)的顺序排列后，若有奇数个数时，则取_____的一个数为中位数；若有偶数个数时，则取中间两个数的_______为中位数．3．众数：一组数据中出现_________的数据，称为该组数据的众数．
一、确定性事件与随机事件1．必然事件：在一定条件下重复进行试验时，在每次试验中_______发生的事件．2．不可能事件：在一定条件下重复进行试验时，在每次试验中_________发生的事件．3．随机事件：在一定条件下，_____________________的事件．