

2021-2022学年浙江省嘉兴市秀洲外国语校中考数学模拟预测试卷含解析
展开
这是一份2021-2022学年浙江省嘉兴市秀洲外国语校中考数学模拟预测试卷含解析,共17页。试卷主要包含了考生必须保证答题卡的整洁,实数 的相反数是等内容,欢迎下载使用。
2021-2022中考数学模拟试卷
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(共10小题,每小题3分,共30分)
1.今年我市计划扩大城区绿地面积,现有一块长方形绿地,它的短边长为60m,若将短边增长到长边相等(长边不变),使扩大后的棣地的形状是正方形,则扩大后的绿地面积比原来增加1600,设扩大后的正方形绿地边长为xm,下面所列方程正确的是( )
A.x(x-60)=1600
B.x(x+60)=1600
C.60(x+60)=1600
D.60(x-60)=1600
2.如图,圆弧形拱桥的跨径米,拱高米,则拱桥的半径为( )米
A. B. C. D.
3.计算 的结果是( )
A.a2 B.-a2 C.a4 D.-a4
4.某青年排球队12名队员年龄情况如下:
年龄
18
19
20
21
22
人数
1
4
3
2
2
则这12名队员年龄的众数、中位数分别是( )
A.20,19 B.19,19 C.19,20.5 D.19,20
5.一个圆的内接正六边形的边长为 2,则该圆的内接正方形的边长为( )
A. B.2 C.2 D.4
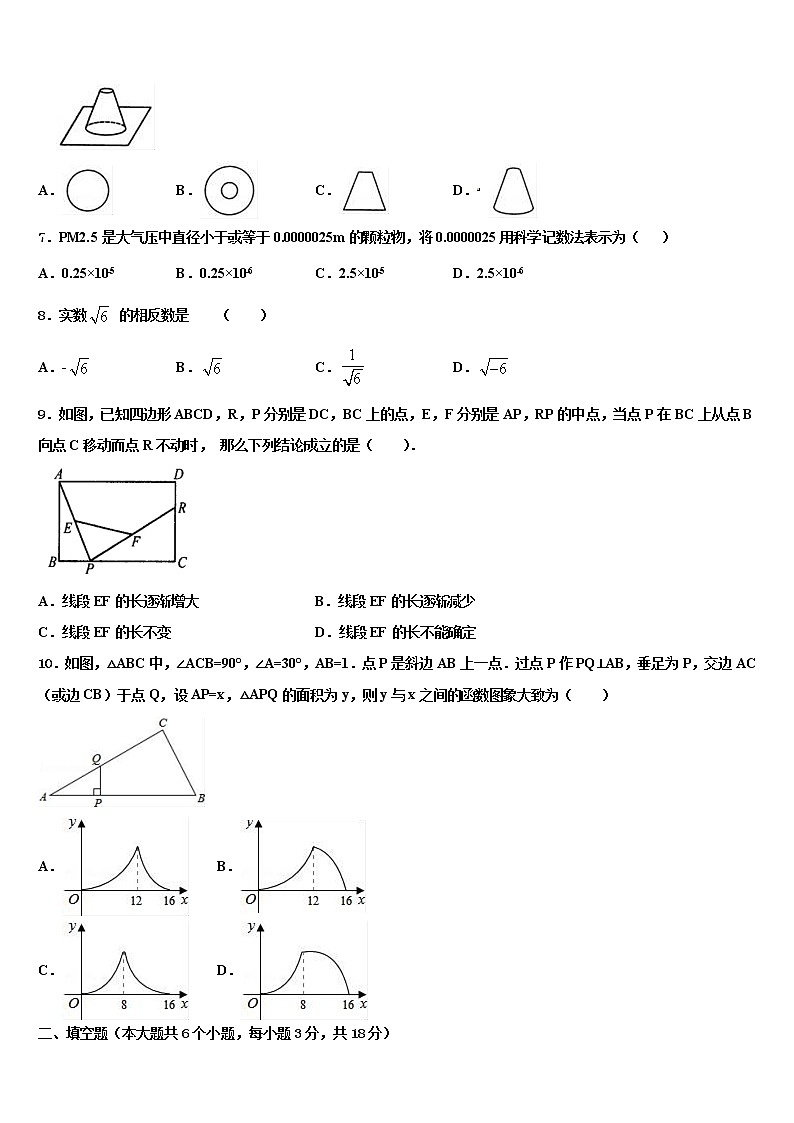
6.如图是一个放置在水平桌面的锥形瓶,它的俯视图是( )
A. B. C. D.
7.PM2.5是大气压中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )
A.0.25×10﹣5 B.0.25×10﹣6 C.2.5×10﹣5 D.2.5×10﹣6
8.实数 的相反数是 ( )
A.- B. C. D.
9.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时, 那么下列结论成立的是( ).
A.线段EF的长逐渐增大 B.线段EF的长逐渐减少
C.线段EF的长不变 D.线段EF的长不能确定
10.如图,△ABC中,∠ACB=90°,∠A=30°,AB=1.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
A. B.
C. D.
二、填空题(本大题共6个小题,每小题3分,共18分)
11.将一次函数y=2x+4的图象向下平移3个单位长度,相应的函数表达式为_____.
12.如图,在平面直角坐标系xOy中,点A,P分别在x轴、y轴上,∠APO=30°.先将线段PA沿y轴翻折得到线段PB,再将线段PA绕点P顺时针旋转30°得到线段PC,连接BC.若点A的坐标为(﹣1,0),则线段BC的长为_____.
13.已知二次函数,与的部分对应值如下表所示:
…
-1
0
1
2
3
4
…
…
6
1
-2
-3
-2
m
…
下面有四个论断:
①抛物线的顶点为;
②;
③关于的方程的解为;
④.
其中,正确的有___________________.
14.如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是_____海里(不近似计算).
15.如图,AB∥CD,BE交CD于点D,CE⊥BE于点E,若∠B=34°,则∠C的大小为________度.
16.如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标(6,0),B的坐标(0,8),点C的坐标(﹣2,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动,动点N从O点开始,以每秒2个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间为t秒(t>0),△OMN的面积为S.则:AB的长是_____,BC的长是_____,当t=3时,S的值是_____.
三、解答题(共8题,共72分)
17.(8分)我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
此次共调查了 名学生;扇形统计图中D所在扇形的圆心角为 ;将上面的条形统计图补充完整;若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数.
18.(8分)某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个.商场想了两个方案来增加利润:
方案一:提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告.已知当这种商品每月的广告费用为m(千元)时,每月销售量将是原销售量的p倍,且p =.
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由!
19.(8分)随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两个统计图.
(1)本次调查的学生共有 人,估计该校1200名学生中“不了解”的人数是 人;
(2)“非常了解”的4人有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
20.(8分)化简分式,并从0、1、2、3这四个数中取一个合适的数作为x的值代入求值.
21.(8分)一个不透明的口袋中装有2个红球、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
22.(10分)某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.
(1)根据图象求出b关于a的函数解析式(包括自变量的取值范围);
(2)若农场到B公司的路程是农场到A公司路程的2倍,农场到A公司的路程为m千米,设农场从A公司购买x吨铵肥,购买8吨铵肥的总费用为y元(总费用=购买铵肥费用+运输费用),求出y关于x的函数解析式(m为常数),并向农场建议总费用最低的购买方案.
23.(12分)赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为________米.
24.在“双十一”购物街中,某儿童品牌玩具专卖店购进了两种玩具,其中类玩具的金价比玩具的进价每个多元.经调查发现:用元购进类玩具的数量与用元购进类玩具的数量相同.求的进价分别是每个多少元?该玩具店共购进了两类玩具共个,若玩具店将每个类玩具定价为元出售,每个类玩具定价元出售,且全部售出后所获得的利润不少于元,则该淘宝专卖店至少购进类玩具多少个?
参考答案
一、选择题(共10小题,每小题3分,共30分)
1、A
【解析】
试题分析:根据题意可得扩建的部分相当于一个长方形,这个长方形的长和宽分别为x米和(x-60)米,根据长方形的面积计算法则列出方程.
考点:一元二次方程的应用.
2、A
【解析】
试题分析:根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O.连接OA.根据垂径定理和勾股定理求解.得AD=6设圆的半径是r, 根据勾股定理, 得r2=36+(r﹣4)2,解得r=6.5
考点:垂径定理的应用.
3、D
【解析】
直接利用同底数幂的乘法运算法则计算得出答案.
【详解】
解:,
故选D.
【点睛】
此题主要考查了同底数幂的乘法运算,正确掌握运算法则是解题关键.
4、D
【解析】
先计算出这个队共有1+4+3+2+2=12人,然后根据众数与中位数的定义求解.
【详解】
这个队共有1+4+3+2+2=12人,这个队队员年龄的众数为19,中位数为=1.
故选D.
【点睛】
本题考查了众数:在一组数据中出现次数最多的数叫这组数据的众数.也考查了中位数的定义.
5、B
【解析】
圆内接正六边形的边长是1,即圆的半径是1,则圆的内接正方形的对角线长是2,进而就可求解.
【详解】
解:∵圆内接正六边形的边长是1,
∴圆的半径为1.
那么直径为2.
圆的内接正方形的对角线长为圆的直径,等于2.
∴圆的内接正方形的边长是1.
故选B.
【点睛】
本题考查正多边形与圆,关键是利用知识点:圆内接正六边形的边长和圆的半径相等;圆的内接正方形的对角线长为圆的直径解答.
6、B
【解析】
根据俯视图是从上面看到的图形解答即可.
【详解】
锥形瓶从上面往下看看到的是两个同心圆.
故选B.
【点睛】
本题考查三视图的知识,解决此类图的关键是由三视图得到相应的平面图形.从正面看到的图是正视图,从上面看到的图形是俯视图,从左面看到的图形是左视图,能看到的线画实线,被遮挡的线画虚线.
7、D
【解析】
根据科学记数法的定义,科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.在确定n的值时,看该数是大于或等于1还是小于1.当该数大于或等于1时,n为它的整数位数减1;当该数小于1时,-n为它第一个有效数字前0的个数(含小数点前的1个0).
【详解】
解: 0.0000025第一个有效数字前有6个0(含小数点前的1个0),从而.
故选D.
8、A
【解析】
根据相反数的定义即可判断.
【详解】
实数 的相反数是-
故选A.
【点睛】
此题主要考查相反数的定义,解题的关键是熟知相反数的定义即可求解.
9、C
【解析】
因为R不动,所以AR不变.根据三角形中位线定理可得EF= AR,因此线段EF的长不变.
【详解】
如图,连接AR,
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF= AR,为定值.
∴线段EF的长不改变.
故选:C.
【点睛】
本题考查了三角形的中位线定理,只要三角形的边AR不变,则对应的中位线的长度就不变.
10、D
【解析】
解:当点Q在AC上时,∵∠A=30°,AP=x,∴PQ=xtan30°=,∴y=×AP×PQ=×x×=x2;
当点Q在BC上时,如下图所示:
∵AP=x,AB=1,∠A=30°,∴BP=1﹣x,∠B=60°,∴PQ=BP•tan60°=(1﹣x),∴ =AP•PQ= = ,∴该函数图象前半部分是抛物线开口向上,后半部分也为抛物线开口向下.故选D.
点睛:本题考查动点问题的函数图象,有一定难度,解题关键是注意点Q在BC上这种情况.
二、填空题(本大题共6个小题,每小题3分,共18分)
11、y=2x+1
【解析】
分析:直接根据函数图象平移的法则进行解答即可.
详解:将一次函数y=2x+4的图象向下平移3个单位长度,相应的函数是y=2x+4-3=2x+1;
故答案为y=2x+1.
点睛:本题考查的是一次函数的图象与几何变换,熟知“上加下减”的法则是解答此题的关键.
12、2
【解析】
只要证明△PBC是等腰直角三角形即可解决问题.
【详解】
解:∵∠APO=∠BPO=30°,
∴∠APB=60°,
∵PA=PC=PB,∠APC=30°,
∴∠BPC=90°,
∴△PBC是等腰直角三角形,
∵OA=1,∠APO=30°,
∴PA=2OA=2,
∴BC=PC=2,
故答案为2.
【点睛】
本题考查翻折变换、坐标与图形的变化、等腰直角三角形的判定和性质等知识,解题的关键是证明△PBC是等腰直角三角形.
13、①③.
【解析】
根据图表求出函数对称轴,再根据图表信息和二次函数性质逐一判断即可.
【详解】
由二次函数y=ax2+bx+c(a≠0),y与x的部分对应值可知:
该函数图象是开口向上的抛物线,对称轴是直线x=2,顶点坐标为(2,-3);与x轴有两个交点,一个在0与1之间,另一个在3与4之间;当y=-2时,x=1或x=3;由抛物线的对称性可知,m=1;
①抛物线y=ax2+bx+c(a≠0)的顶点为(2,-3),结论正确;
②b2﹣4ac=0,结论错误,应该是b2﹣4ac>0;
③关于x的方程ax2+bx+c=﹣2的解为x1=1,x2=3,结论正确;
④m=﹣3,结论错误,
其中,正确的有. ①③
故答案为:①③
【点睛】
本题考查了二次函数的图像,结合图表信息是解题的关键.
14、6
【解析】
试题分析:过S作AB的垂线,设垂足为C.根据三角形外角的性质,易证SB=AB.在Rt△BSC中,运用正弦函数求出SC的长.
解:过S作SC⊥AB于C.
∵∠SBC=60°,∠A=30°,
∴∠BSA=∠SBC﹣∠A=30°,
即∠BSA=∠A=30°.
∴SB=AB=1.
Rt△BCS中,BS=1,∠SBC=60°,
∴SC=SB•sin60°=1×=6(海里).
即船继续沿正北方向航行过程中距灯塔S的最近距离是6海里.
故答案为:6.
15、56
【解析】
解:∵AB∥CD,
∴
又∵CE⊥BE,
∴Rt△CDE中,
故答案为56.
16、10, 1, 1
【解析】
作CD⊥x轴于D,CE⊥OB于E,由勾股定理得出AB=10,OC==1,求出BE=OB﹣OE=4,得出OE=BE,由线段垂直平分线的性质得出BC=OC=1;当t=3时,N到达C点,M到达OA的中点,OM=3,ON=OC=1,由三角形面积公式即可得出△OMN的面积.
【详解】
解:作CD⊥x轴于D,CE⊥OB于E,如图所示:
由题意得:OA=1,OB=8,
∵∠AOB=90°,
∴AB==10;
∵点C的坐标(﹣2,4),
∴OC==1,OE=4,
∴BE=OB﹣OE=4,
∴OE=BE,
∴BC=OC=1;当t=3时,N到达C点,M到达OA的中点,OM=3,ON=OC=1,
∴△OMN的面积S=×3×4=1;
故答案为:10,1,1.
【点睛】
本题考查了勾股定理、坐标与图形性质、线段垂直平分线的性质、三角形面积公式等知识;熟练掌握勾股定理是解题的关键.
三、解答题(共8题,共72分)
17、(1)120;(2)54°;(3)详见解析(4)1.
【解析】
(1)根据B的人数除以占的百分比即可得到总人数;
(2)先根据题意列出算式,再求出即可;
(3)先求出对应的人数,再画出即可;
(4)先列出算式,再求出即可.
【详解】
(1)(25+23)÷40%=120(名),
即此次共调查了120名学生,
故答案为120;
(2)360°×=54°,
即扇形统计图中D所在扇形的圆心角为54°,
故答案为54°;
(3)如图所示:
;
(4)800×=1(人),
答:估计对食品安全知识“非常了解”的学生的人数是1人.
【点睛】
本题考查了条形统计图、扇形统计图,总体、个体、样本、样本容量,用样本估计总体等知识点,两图结合是解题的关键.
18、方案二能获得更大的利润;理由见解析
【解析】
方案一:由利润=(实际售价-进价)×销售量,列出函数关系式,再用配方法求最大利润;
方案二:由利润=(售价-进价)×500p-广告费用,列出函数关系式,再用配方法求最大利润.
【详解】
解:设涨价x元,利润为y元,则
方案一:涨价x元时,该商品每一件利润为:50+x−40,销售量为:500−10x,
∴,
∵当x=20时,y最大=9000,
∴方案一的最大利润为9000元;
方案二:该商品售价利润为=(50−40)×500p,广告费用为:1000m元,
∴,
∴方案二的最大利润为10125元;
∴选择方案二能获得更大的利润.
【点睛】
本题考查二次函数的实际应用,根据题意,列出函数关系式,配方求出最大值.
19、(1)50,360;(2) .
【解析】
试题分析:(1)根据图示,可由非常了解的人数和所占的百分比直接求解总人数,然后根据求出不了解的百分比估计即可;
(2)根据题意画出树状图,然后求出总可能和“一男一女”的可能,再根据概率的意义求解即可.
试题解析:(1)由饼图可知“非常了解”为8%,由柱形图可知(条形图中可知)“非常了解”为4人,故本次调查的学生有(人)
由饼图可知:“不了解”的概率为,故1200名学生中“不了解”的人数为(人)
(2)树状图:
由树状图可知共有12种结果,抽到1男1女分别为共8种.
∴
考点:1、扇形统计图,2、条形统计图,3、概率
20、x取0时,为1 或x取1时,为2
【解析】
试题分析:利用分式的运算,先对分式化简单,再选择使分式有意义的数代入求值即可.
试题解析:解:原式=[]
=
=
= x+1,
∵x1-4≠0,x-2≠0,
∴x≠1且x≠-1且x≠2,
当x=0时,原式=1.
或当x=1时,原式=2.
21、
【解析】
分析:列表得出所有等可能的情况数,找出两次都摸到红球的情况数,即可求出所求的概率.
详解:列表如下:
红
红
白
黑
红
﹣﹣﹣
(红,红)
(白,红)
(黑,红)
红
(红,红)
﹣﹣﹣
(白,红)
(黑,红)
白
(红,白)
(红,白)
﹣﹣﹣
(黑,白)
黑
(红,黑)
(红,黑)
(白,黑)
﹣﹣﹣
所有等可能的情况有12种,其中两次都摸到红球有2种可能,
则P(两次摸到红球)==.
点睛:此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
22、(1)b=;(2)详见解析.
【解析】
(1)分别设两段函数图象的解析式,代入图象上点的坐标求解即可;
(2)先求出农场从A、B公司购买铵肥的费用,再求出农场从A、B公司购买铵肥的运输费用,两者之和即为总费用,可以求出总费用关于x的解析式是一次函数,根据m的取值范围不同分两类讨论,可得出结论.
【详解】
(1)有图象可得,函数图象分为两部分,设第一段函数图象为y=k1x,代入点(4,12),即12=k1×4,可得k1=3,设第二段函数图象为y=k2x+c,代入点(4,12)、(8,32)可列出二元一次方程组,解得:k2=5,c=-8,所以函数解析式为:b=;
(2)农场从A公司购买铵肥的费用为750x元,因为B公司有铵肥7吨,1≤x≤3,故农场从B公司购买铵肥的重量(8-x)肯定大于5吨,农场从B公司购买铵肥的费用为700(8-x)元,所以购买铵肥的总费用=750x+700(8-x)=50x+5600(0≤x≤3);农场从A公司购买铵肥的运输费用为3xm元,且满足1≤x≤3,农场从B公司购买铵肥的运输费用为[5(8-x)-8]×2m元,所以购买铵肥的总运输费用为3xm+[5(8-x)-8]×2m=-7mx+64m元,因此农场购买铵肥的总费用y=50x+5600-7mx+64m=(50-7m)x+5600+64m(1≤x≤3),分一下两种情况进行讨论;
①当50-7m≥0即m≤时,y随x的增加而增加,则x=1使得y取得最小值即总费用最低,此时农场铵肥的购买方案为:从A公司购买1吨,从B公司购买7吨,
②当50-7m<0即m>时,y随x的增加而减少,则x=3使得y取得最小值即总费用最低,此时农场铵肥的购买方案为:从A公司购买3吨,从B公司购买5吨.
【点睛】
本题主要考查了方案比较以及函数解析式的求解,解本题的要点在于根据题意列出相关方程式.
23、10
【解析】
试题分析:根据相似的性质可得:1:1.2=x:9.6,则x=8,则旗杆的高度为8+2=10米.
考点:相似的应用
24、(1)的进价是元,的进价是元;(2)至少购进类玩具个.
【解析】
(1)设的进价为元,则的进价为元,根据用元购进类玩具的数量与用元购进类玩具的数量相同这个等量关系列出方程即可;
(2)设玩具个,则玩具个,结合“玩具点将每个类玩具定价为元出售,每个类玩具定价元出售,且全部售出后所获得利润不少于元”列出不等式并解答.
【详解】
解:(1)设的进价为元,则的进价为元
由题意得,
解得,
经检验是原方程的解.
所以(元)
答:的进价是元,的进价是元;
(2)设玩具个,则玩具个
由题意得:
解得.
答:至少购进类玩具个.
【点睛】
本题考查了分式方程的应用和一元一次不等式的应用.解决本题的关键是读懂题意,找到符合题意的数量关系,准确的解分式方程或不等式是需要掌握的基本计算能力.
相关试卷
这是一份2023年浙江省嘉兴市上海外国语大学秀洲外国语学校中考数学二模试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年浙江省嘉兴市上海外国语大学秀洲外国语学校中考数学二模试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年浙江省嘉兴市上海外国语大学秀洲外国语学校中考数学一模试卷,共34页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









