2022届广东省茂名市行知中学中考数学模拟预测试卷含解析

这是一份2022届广东省茂名市行知中学中考数学模拟预测试卷含解析，共25页。试卷主要包含了对于一组统计数据，我们知道等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．下列计算正确的是
A．a2·a2＝2a4 B．(－a2)3＝－a6 C．3a2－6a2＝3a2 D．(a－2)2＝a2－4
2．两个有理数的和为零，则这两个数一定是（　　）
A．都是零 B．至少有一个是零
C．一个是正数，一个是负数 D．互为相反数
3．已知关于x的二次函数y＝x2﹣2x﹣2，当a≤x≤a+2时，函数有最大值1，则a的值为（　　）
A．﹣1或1 B．1或﹣3 C．﹣1或3 D．3或﹣3
4．如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的角平分线分别交AB，BD于M，N两点．若AM＝2，则线段ON的长为( )

A． B． C．1 D．
5．如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH=（ ）

A． B． C．12 D．24
6．对于一组统计数据：1，6，2，3，3，下列说法错误的是( )
A．平均数是3 B．中位数是3 C．众数是3 D．方差是2.5
7．我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为4的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为(　　)

A．(，2) B．(4，1) C．(4，) D．(4，)
8．实数a、b、c在数轴上的位置如图所示，则代数式|c﹣a|﹣|a+b|的值等于（　　）

A．c+b B．b﹣c C．c﹣2a+b D．c﹣2a﹣b
9．如图，取一张长为、宽为的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边应满足的条件是（ ）

A． B． C． D．
10．若关于x的一元二次方程(k－1)x2＋4x＋1＝0有两个不相等的实数根，则k的取值范围是( )
A．k<5 B．k<5，且k≠1 C．k≤5，且k≠1 D．k>5
二、填空题（共7小题，每小题3分，满分21分）
11．如图，四边形ABCD是菱形，☉O经过点A，C，D，与BC相交于点E，连接AC，AE，若∠D=78°，则∠EAC=________°.

12．如图，在△ABC中，∠C＝90°，BC＝16 cm，AC＝12 cm，点P从点B出发，沿BC以2 cm/s的速度向点C移动，点Q从点C出发，以1 cm/s的速度向点A移动，若点P、Q分别从点B、C同时出发，设运动时间为ts，当t＝__________时，△CPQ与△CBA相似．

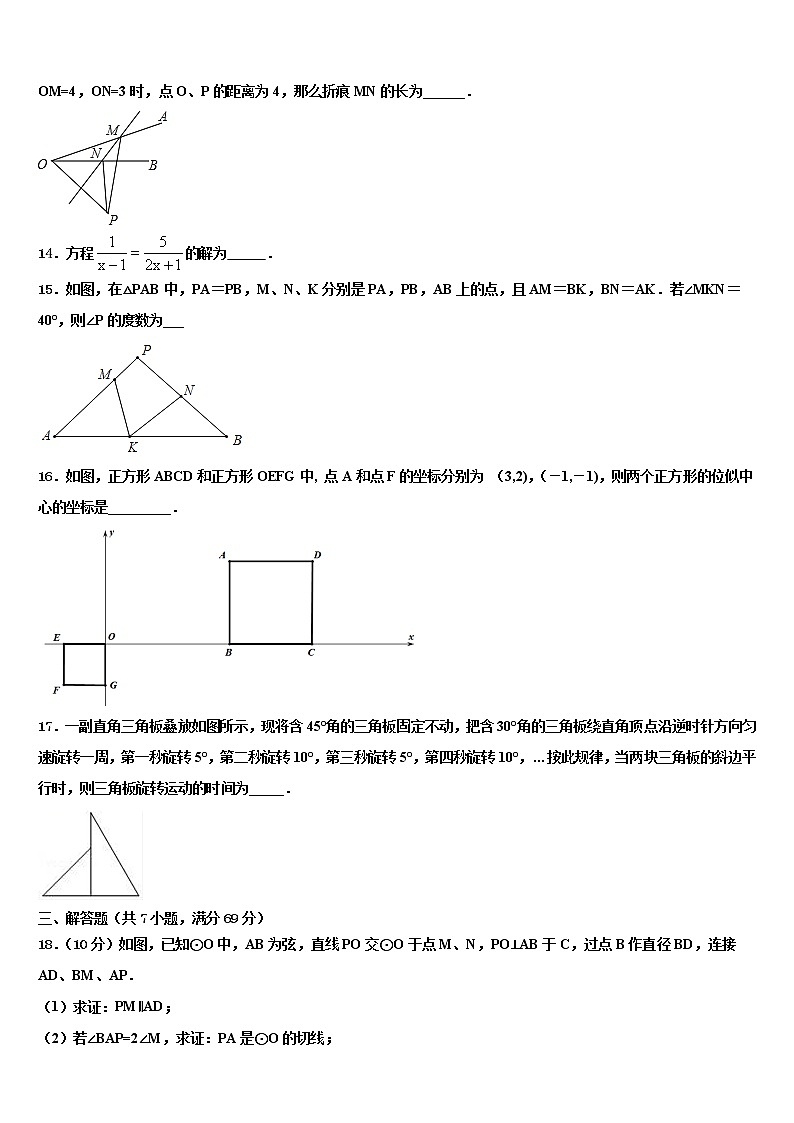
13．如图，点M、N分别在∠AOB的边OA、OB上，将∠AOB沿直线MN翻折，设点O落在点P处，如果当OM=4，ON=3时，点O、P的距离为4，那么折痕MN的长为______．

14．方程的解为　 　 ．
15．如图，在△PAB中，PA＝PB，M、N、K分别是PA，PB，AB上的点，且AM＝BK，BN＝AK．若∠MKN＝40°，则∠P的度数为___

16．如图，正方形ABCD和正方形OEFG中, 点A和点F的坐标分别为 （3,2)，（－1,－1)，则两个正方形的位似中心的坐标是_________．

17．一副直角三角板叠放如图所示，现将含45°角的三角板固定不动，把含30°角的三角板绕直角顶点沿逆时针方向匀速旋转一周，第一秒旋转5°，第二秒旋转10°，第三秒旋转5°，第四秒旋转10°，…按此规律，当两块三角板的斜边平行时，则三角板旋转运动的时间为_____．

三、解答题（共7小题，满分69分）
18．（10分）如图，已知⊙O中，AB为弦，直线PO交⊙O于点M、N，PO⊥AB于C，过点B作直径BD，连接AD、BM、AP．
（1）求证：PM∥AD；
（2）若∠BAP=2∠M，求证：PA是⊙O的切线；
（3）若AD=6，tan∠M=，求⊙O的直径．

19．（5分）如图，在△ABC中，∠ACB＝90°，∠ABC＝10°，△CDE是等边三角形，点D在边AB上．
如图1，当点E在边BC上时，求证DE＝EB；如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；如图1，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG＝5CG，BH＝1．求CG的长．
20．（8分）先化简，再求值：，其中满足．
21．（10分）如图1，已知直线y=kx与抛物线y=交于点A（3，6）．
（1）求直线y=kx的解析式和线段OA的长度；
（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；
（3）如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？

22．（10分）如图，平行四边形ABCD的对角线AC，BD相交于点O，EF过点O且与AB、CD分别交于点E、F．求证：OE＝OF．

23．（12分）如图，正方形ABCD的边长为4，点E，F分别在边AB，AD上，且∠ECF＝45°，CF的延长线交BA的延长线于点G，CE的延长线交DA的延长线于点H，连接AC，EF．，GH．

（1）填空：∠AHC　 　∠ACG；（填“＞”或“＜”或“＝”）
（2）线段AC，AG，AH什么关系？请说明理由；
（3）设AE＝m，
①△AGH的面积S有变化吗？如果变化．请求出S与m的函数关系式；如果不变化，请求出定值．
②请直接写出使△CGH是等腰三角形的m值．
24．（14分）如图，在△ABC中，∠C＝90°，∠CAB＝50°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为( )

A．40° B．55° C．65° D．75°



参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、B
【解析】【分析】根据同底数幂乘法、幂的乘方、合并同类项法则、完全平方公式逐项进行计算即可得.
【详解】A. a2·a2＝a4 ，故A选项错误；
B. (－a2)3＝－a6 ，正确；
C. 3a2－6a2＝-3a2 ，故C选项错误；
D. (a－2)2＝a2－4a+4，故D选项错误，
故选B.
【点睛】本题考查了同底数幂的乘法、幂的乘方、合并同类项、完全平方公式，熟练掌握各运算的运算法则是解题的关键.
2、D
【解析】
解：互为相反数的两个有理数的和为零，故选D．A、C不全面．B、不正确．
3、A
【解析】
分析：
详解：∵当a≤x≤a＋2时，函数有最大值1，∴1＝x2－2x－2,解得： ，
即-1≤x≤3, ∴a=-1或a+2=-1, ∴a=-1或1，故选A.
点睛：本题考查了求二次函数的最大(小)值的方法，注意：只有当自变量x在整个取值范围内，函数值y才在顶点处取最值，而当自变量取值范围只有一部分时，必须结合二次函数的增减性及对称轴判断何处取最大值，何处取最小值.
4、C
【解析】
作MH⊥AC于H，如图，根据正方形的性质得∠MAH=45°，则△AMH为等腰直角三角形，所以AH=MH=AM=，再根据角平分线性质得BM=MH=，则AB=2+，于是利用正方形的性质得到AC=AB=2+2，OC=AC=+1，所以CH=AC-AH=2+，然后证明△CON∽△CHM，再利用相似比可计算出ON的长．
【详解】
试题分析：作MH⊥AC于H，如图，

∵四边形ABCD为正方形，
∴∠MAH=45°，
∴△AMH为等腰直角三角形，
∴AH=MH=AM=×2=，
∵CM平分∠ACB，
∴BM=MH=，
∴AB=2+，
∴AC=AB=（2+）=2+2，
∴OC=AC=+1，CH=AC﹣AH=2+2﹣=2+，
∵BD⊥AC，
∴ON∥MH，
∴△CON∽△CHM，
∴，即，
∴ON=1．
故选C．
【点睛】
本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．也考查了角平分线的性质和正方形的性质．
5、A
【解析】
解：如图，设对角线相交于点O，
∵AC=8，DB=6，∴AO=AC=×8=4，BO=BD=×6=3，
由勾股定理的，AB===5，
∵DH⊥AB，∴S菱形ABCD=AB•DH=AC•BD，
即5DH=×8×6，解得DH=．
故选A．

【点睛】
本题考查菱形的性质．
6、D
【解析】
根据平均数、中位数、众数和方差的定义逐一求解可得．
【详解】
解：A、平均数为=3，正确；
B、重新排列为1、2、3、3、6，则中位数为3，正确；
C、众数为3，正确；
D、方差为×[（1-3）2+（6-3）2+（2-3）2+（3-3）2+（3-3）2]=2.8，错误；
故选：D．
【点睛】
本题考查了众数、平均数、中位数、方差．平均数平均数表示一组数据的平均程度．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；方差是用来衡量一组数据波动大小的量．
7、D
【解析】
由已知条件得到AD′=AD=4，AO=AB=2，根据勾股定理得到OD′= =2，于是得到结论．
【详解】
解：∵AD′=AD=4，
AO=AB=1，
∴OD′==2，
∵C′D′=4，C′D′∥AB，
∴C′（4，2），
故选：D．
【点睛】
本题考查正方形的性质，坐标与图形的性质，勾股定理，正确的识别图形是解题关键．
8、A
【解析】
根据数轴得到b＜a＜0＜c，根据有理数的加法法则，减法法则得到c-a＞0，a+b＜0，根据绝对值的性质化简计算．
【详解】
由数轴可知，b＜a＜0＜c，
∴c-a＞0，a+b＜0，
则|c-a|-|a+b|=c-a+a+b=c+b，
故选A．
【点睛】
本题考查的是实数与数轴，绝对值的性质，能够根据数轴比较实数的大小，掌握绝对值的性质是解题的关键．
9、B
【解析】
由题图可知：得对折两次后得到的小长方形纸片的长为，宽为，然后根据相似多边形的定义，列出比例式即可求出结论．
【详解】
解：由题图可知：得对折两次后得到的小长方形纸片的长为，宽为，
∵小长方形与原长方形相似，


故选B．
【点睛】
此题考查的是相似三角形的性质，根据相似三角形的定义列比例式是解决此题的关键．
10、B
【解析】
试题解析：∵关于x的一元二次方程方程有两个不相等的实数根，∴，即，解得：k＜5且k≠1．故选B．

二、填空题（共7小题，每小题3分，满分21分）
11、1．
【解析】
解:∵四边形ABCD是菱形，∠D=78°，
∴∠ACB=（180°-∠D）=51°，
又∵四边形AECD是圆内接四边形，
∴∠AEB=∠D=78°，
∴∠EAC=∠AEB-∠ACB=1°.
故答案为:1°
12、4.8或
【解析】
根据题意可分两种情况，①当CP和CB是对应边时，△CPQ∽△CBA与②CP和CA是对应边时，△CPQ∽△CAB，根据相似三角形的性质分别求出时间t即可.
【详解】
①CP和CB是对应边时，△CPQ∽△CBA，
所以＝，
即＝，
解得t＝4.8；
②CP和CA是对应边时，△CPQ∽△CAB，
所以＝，
即＝，
解得t＝.
综上所述，当t＝4.8或时，△CPQ与△CBA相似．
【点睛】
此题主要考查相似三角形的性质，解题的关键是分情况讨论.
13、
【解析】
由折叠的性质可得MN⊥OP，EO=EP=2，由勾股定理可求ME，NE的长，即可求MN的长．
【详解】
设MN与OP交于点E，

∵点O、P的距离为4，
∴OP=4
∵折叠
∴MN⊥OP，EO=EP=2，
在Rt△OME中，ME=
在Rt△ONE中，NE=
∴MN=ME-NE=2-
故答案为2-
【点睛】
本题考查了翻折变换，勾股定理，利用勾股定理求线段的长度是本题的关键．
14、．
【解析】
试题分析：首先去掉分母，观察可得最简公分母是，方程两边乘最简公分母，可以把分式方程转化为整式方程求解，然后解一元一次方程，最后检验即可求解：
，经检验，是原方程的根．
15、100°
【解析】
由条件可证明△AMK≌△BKN，再结合外角的性质可求得∠A＝∠MKN，再利用三角形内角和可求得∠P．
【详解】
解：∵PA＝PB，
∴∠A＝∠B，
在△AMK和△BKN中，
，
∴△AMK≌△BKN（SAS），
∴∠AMK＝∠BKN，
∵∠A+∠AMK＝∠MKN+∠BKN，
∴∠A＝∠MKN＝40°，
∴∠P＝180°﹣∠A﹣∠B＝180°﹣40°﹣40°＝100°，
故答案为100°
【点睛】
本题主要考查全等三角形的判定和性质及三角形内角和定理，利用条件证得△AMK≌△BKN是解题的关键．
16、（1，0）；（﹣5，﹣2）.
【解析】
本题主要考查位似变换中对应点的坐标的变化规律．因而本题应分两种情况讨论，一种是当E和C是对应顶点，G和A是对应顶点；另一种是A和E是对应顶点，C和G是对应顶点．
【详解】
∵正方形ABCD和正方形OEFG中A和点F的坐标分别为（3，2），（-1，-1），
∴E（-1，0）、G（0，-1）、D（5，2）、B（3，0）、C（5，0），
（1）当E和C是对应顶点，G和A是对应顶点时，位似中心就是EC与AG的交点，
设AG所在直线的解析式为y=kx+b（k≠0），
∴，解得．
∴此函数的解析式为y=x-1，与EC的交点坐标是（1，0）；
（2）当A和E是对应顶点，C和G是对应顶点时，位似中心就是AE与CG的交点，
设AE所在直线的解析式为y=kx+b（k≠0），
，解得，
故此一次函数的解析式为…①，
同理，设CG所在直线的解析式为y=kx+b（k≠0），
，解得，
故此直线的解析式为…②
联立①②得
解得，故AE与CG的交点坐标是（-5，-2）．
故答案为：（1，0）、（-5，-2）．
17、14s或38s．
【解析】
试题解析：分两种情况进行讨论:
如图：




旋转的度数为：
每两秒旋转


如图：





旋转的度数为：
每两秒旋转


故答案为14s或38s.

三、解答题（共7小题，满分69分）
18、（1）证明见解析；（2）证明见解析；（3）1；
【解析】
（1）根据平行线的判定求出即可；（2）连接OA，求出∠OAP=∠BAP+∠OAB=∠BOC+∠OBC=90°，根据切线的判定得出即可；（3）设BC=x，CM=2x，根据相似三角形的性质和判定求出NC=x，求出MN=2x+x=2.1x，OM=MN=1.21x，OC=0.71x，根据三角形的中位线性质得出0.71x=AD=3，求出x即可．
【详解】
（1）∵BD是直径，
∴∠DAB=90°，
∵PO⊥AB，
∴∠DAB=∠MCB=90°，
∴PM∥AD；
（2）连接OA，
∵OB=OM，
∴∠M=∠OBM，
∴∠BON=2∠M，
∵∠BAP=2∠M，
∴∠BON=∠BAP，
∵PO⊥AB，
∴∠ACO=90°，
∴∠AON+∠OAC=90°，
∵OA=OB，
∴∠BON=∠AON，
∴∠BAP=∠AON，
∴∠BAP+∠OAC=90°，
∴∠OAP=90°，
∵OA是半径，
∴PA是⊙O的切线；
（3）连接BN，
则∠MBN=90°．
∵tan∠M=，
∴=，
设BC=x，CM=2x，
∵MN是⊙O直径，NM⊥AB，
∴∠MBN=∠BCN=∠BCM=90°，
∴∠NBC=∠M=90°﹣∠BNC，
∴△MBC∽△BNC，
∴，
∴BC2=NC×MC，
∴NC=x，
∴MN=2x+x=2.1x，
∴OM=MN=1.21x，
∴OC=2x﹣1.21x=0.71x，
∵O是BD的中点，C是AB的中点，AD=6，
∴OC=0.71x=AD=3，
解得：x=4，
∴MO=1.21x=1.21×4=1，
∴⊙O的半径为1．

【点睛】
本题考查了圆周角定理，切线的性质和判定，相似三角形的性质和判定等知识点，能灵活运用知识点进行推理是解此题的关键，此题有一定的难度．
19、（1）证明见解析；（2）ED=EB，证明见解析；（1）CG=2．
【解析】
(1)、根据等边三角形的性质得出∠CED=60°，从而得出∠EDB=10°，从而得出DE=BE；
(2)、取AB的中点O，连接CO、EO，根据△ACO和△CDE为等边三角形，从而得出△ACD和△OCE全等，然后得出△COE和△BOE全等，从而得出答案；
(1)、取AB的中点O，连接CO、EO、EB，根据题意得出△COE和△BOE全等，然后得出△CEG和△DCO全等，设CG=a，则AG=5a，OD=a，根据题意列出一元一次方程求出a的值得出答案．
【详解】
(1)∵△CDE是等边三角形，
∴∠CED=60°，
∴∠EDB=60°﹣∠B=10°，
∴∠EDB=∠B，
∴DE=EB；
(2) ED=EB， 理由如下：
取AB的中点O，连接CO、EO，
∵∠ACB=90°，∠ABC=10°，
∴∠A=60°，OC=OA，
∴△ACO为等边三角形，
∴CA=CO，
∵△CDE是等边三角形，
∴∠ACD=∠OCE，
∴△ACD≌△OCE，
∴∠COE=∠A=60°，
∴∠BOE=60°，
∴△COE≌△BOE，
∴EC=EB，
∴ED=EB；
(1)、取AB的中点O，连接CO、EO、EB， 由（2）得△ACD≌△OCE，
∴∠COE=∠A=60°，
∴∠BOE=60°，△COE≌△BOE，
∴EC=EB，
∴ED=EB，
∵EH⊥AB，
∴DH=BH=1，
∵GE∥AB，
∴∠G=180°﹣∠A=120°，
∴△CEG≌△DCO，
∴CG=OD，
设CG=a，则AG=5a，OD=a，
∴AC=OC=4a，
∵OC=OB，
∴4a=a+1+1，
解得，a=2，
即CG=2．

20、，1．
【解析】
原式括号中的两项通分并利用同分母分式的加法法则计算，再与括号外的分式通分后利用同分母分式的加法法则计算，约分得到最简结果，将变形为，整体代入计算即可．
【详解】
解：原式





∵，
∴，
∴原式
【点睛】
本题主要考查分式的化简求值，解题的关键是掌握分式的混合运算顺序和运算法则．
21、（1）y=2x，OA=，
（2）是一个定值，，
（3）当时，E点只有1个，当时，E点有2个。
【解析】（1）把点A（3，6）代入y=kx 得；
∵6=3k，
∴k=2，
∴y=2x．
OA=．
（2）是一个定值，理由如下：
如答图1，过点Q作QG⊥y轴于点G，QH⊥x轴于点H．

①当QH与QM重合时，显然QG与QN重合，
此时；
②当QH与QM不重合时，
∵QN⊥QM，QG⊥QH
不妨设点H，G分别在x、y轴的正半轴上，
∴∠MQH=∠GQN，
又∵∠QHM=∠QGN=90°
∴△QHM∽△QGN…（5分），
∴，
当点P、Q在抛物线和直线上不同位置时，同理可得．①①
如答图2，延长AB交x轴于点F，过点F作FC⊥OA于点C，过点A作AR⊥x轴于点R

∵∠AOD=∠BAE，
∴AF=OF，
∴OC=AC=OA=
∵∠ARO=∠FCO=90°，∠AOR=∠FOC，
∴△AOR∽△FOC，
∴，
∴OF=，
∴点F（，0），
设点B（x，），
过点B作BK⊥AR于点K，则△AKB∽△ARF，
∴，
即，
解得x1=6，x2=3（舍去），
∴点B（6，2），
∴BK=6﹣3=3，AK=6﹣2=4，
∴AB=5
（求AB也可采用下面的方法）
设直线AF为y=kx+b（k≠0）把点A（3，6），点F（，0）代入得
k=，b=10，
∴，
∴，
∴（舍去），，
∴B（6，2），
∴AB=5
在△ABE与△OED中
∵∠BAE=∠BED，
∴∠ABE+∠AEB=∠DEO+∠AEB，
∴∠ABE=∠DEO，
∵∠BAE=∠EOD，
∴△ABE∽△OED.
设OE=x，则AE=﹣x （），
由△ABE∽△OED得，
∴
∴（）
∴顶点为（，）
如答图3，

当时，OE=x=，此时E点有1个；
当时，任取一个m的值都对应着两个x值，此时E点有2个．
∴当时，E点只有1个
当时，E点有2个
22、见解析
【解析】
由四边形ABCD是平行四边形,根据平行四边形对角线互相平分,即可得OA=OC,易证得△AEO≌△CFO,由全等三角形的对应边相等,可得OE=OF．
【详解】
证明：∵四边形ABCD是平行四边形,
∴OA=OC,AB∥DC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
∴△AEO≌△CFO(ASA),
∴OE=OF.
【点睛】
本题考查了平行四边形的性质和全等三角形的判定,属于简单题,熟悉平行四边形的性质和全等三角形的判定方法是解题关键.
23、（1）=；（2）结论：AC2＝AG•AH．理由见解析；（3）①△AGH的面积不变．②m的值为或2或8﹣4．.
【解析】
（1）证明∠DAC=∠AHC+∠ACH=43°，∠ACH+∠ACG=43°，即可推出∠AHC=∠ACG；
（2）结论：AC2=AG•AH．只要证明△AHC∽△ACG即可解决问题；
（3）①△AGH的面积不变．理由三角形的面积公式计算即可；
②分三种情形分别求解即可解决问题.
【详解】
（1）∵四边形ABCD是正方形，
∴AB＝CB＝CD＝DA＝4，∠D＝∠DAB＝90°∠DAC＝∠BAC＝43°，
∴AC＝，
∵∠DAC＝∠AHC+∠ACH＝43°，∠ACH+∠ACG＝43°，
∴∠AHC＝∠ACG．
故答案为＝．
（2）结论：AC2＝AG•AH．
理由：∵∠AHC＝∠ACG，∠CAH＝∠CAG＝133°，
∴△AHC∽△ACG，
∴，
∴AC2＝AG•AH．
（3）①△AGH的面积不变．
理由：∵S△AGH＝•AH•AG＝AC2＝×（4）2＝1．
∴△AGH的面积为1．
②如图1中，当GC＝GH时，易证△AHG≌△BGC，

可得AG＝BC＝4，AH＝BG＝8，
∵BC∥AH，
∴,
∴AE＝AB＝．
如图2中，当CH＝HG时，

易证AH＝BC＝4，
∵BC∥AH，
∴＝1，
∴AE＝BE＝2．
如图3中，当CG＝CH时，易证∠ECB＝∠DCF＝22.3．

在BC上取一点M，使得BM＝BE，
∴∠BME＝∠BEM＝43°，
∵∠BME＝∠MCE+∠MEC，
∴∠MCE＝∠MEC＝22.3°，
∴CM＝EM，设BM＝BE＝m，则CM＝EMm，
∴m+m＝4，
∴m＝4（﹣1），
∴AE＝4﹣4（﹣1）＝8﹣4，
综上所述，满足条件的m的值为或2或8﹣4．
【点睛】
本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题．
24、C．
【解析】
试题分析：由作图方法可得AG是∠CAB的角平分线，
∵∠CAB=50°，∴∠CAD=∠CAB=25°，∵∠C=90°，∴∠CDA=90°﹣25°=65°，
故选C．
考点：作图—基本作图．