2022届海南省海南中学中考数学最后冲刺模拟试卷含解析

这是一份2022届海南省海南中学中考数学最后冲刺模拟试卷含解析，共20页。试卷主要包含了如图所示的几何体的俯视图是，不等式组的解在数轴上表示为等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
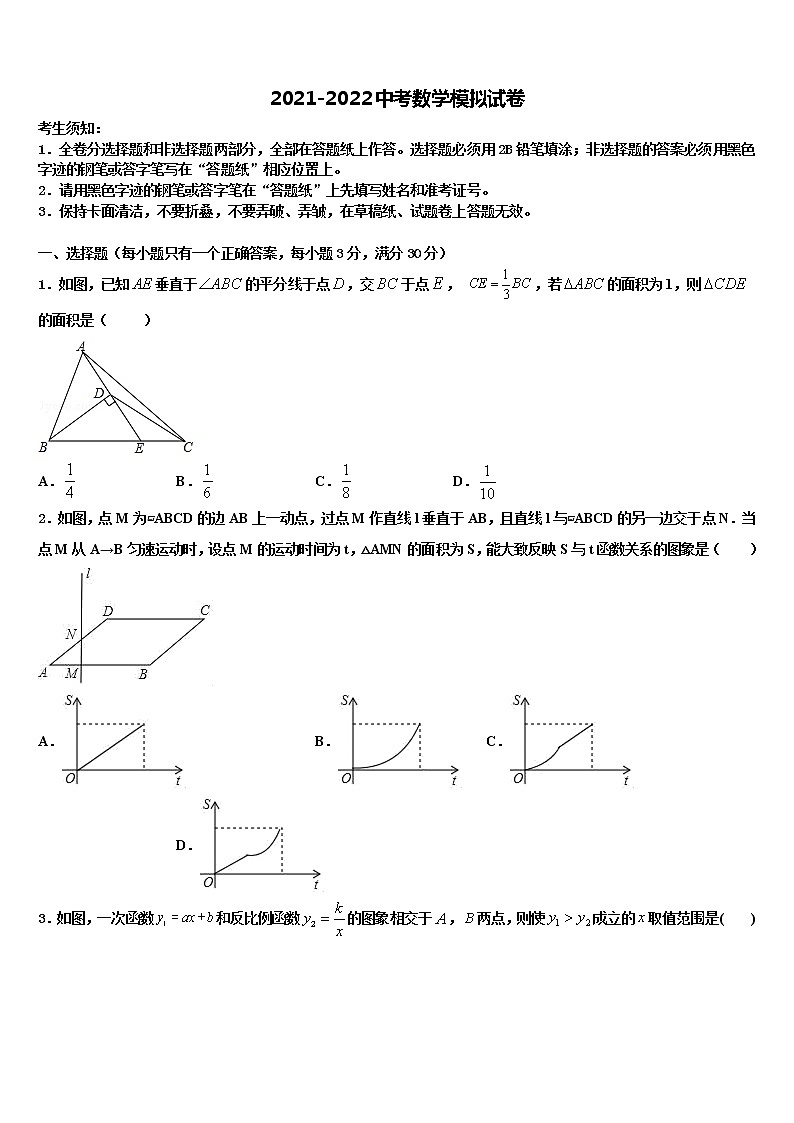
1．如图，已知垂直于的平分线于点，交于点， ，若的面积为1，则的面积是（ ）

A． B． C． D．
2．如图，点M为▱ABCD的边AB上一动点，过点M作直线l垂直于AB，且直线l与▱ABCD的另一边交于点N．当点M从A→B匀速运动时，设点M的运动时间为t，△AMN的面积为S，能大致反映S与t函数关系的图象是（　　）

A． B． C． D．
3．如图，一次函数和反比例函数的图象相交于，两点，则使成立的取值范围是(　　)

A．或 B．或
C．或 D．或
4．在，，，这四个数中，比小的数有（ ）个．
A． B． C． D．
5．如图，两个一次函数图象的交点坐标为，则关于x，y的方程组的解为（ ）

A． B． C． D．
6．如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P．若点P的坐标为（2a，b+1），则a与b的数量关系为

A．a=b B．2a+b=﹣1 C．2a﹣b=1 D．2a+b=1
7．（2016四川省甘孜州）如图，在5×5的正方形网格中，每个小正方形的边长都为1，若将△AOB绕点O顺时针旋转90°得到△A′OB′，则A点运动的路径的长为（　　）

A．π B．2π C．4π D．8π
8．如图所示的几何体的俯视图是（　　）

A． B． C． D．
9．如图所示的两个四边形相似，则α的度数是(　　)

A．60° B．75° C．87° D．120°
10．不等式组的解在数轴上表示为（ ）
A． B． C． D．
二、填空题（共7小题，每小题3分，满分21分）
11．如图，AC是正五边形ABCDE的一条对角线，则∠ACB＝_____．

12．若4a+3b=1，则8a+6b-3的值为______.
13．在某公益活动中，小明对本年级同学的捐款情况进行了统计，绘制成如图所示的不完整的统计图，其中捐10元的人数占年级总人数的25%，则本次捐款20元的人数为______ 人．

14．已知△ABC中，BC=4，AB=2AC，则△ABC面积的最大值为_______．

15．分解因式：=______．
16．如图，在△ABC中，∠B＝40°，∠C＝45°，AB的垂直平分线交BC于点D，AC的垂直平分线交BC于点E，则∠DAE＝______．

17．化简：a+1+a（a+1）+a（a+1）2+…+a（a+1）99=________．
三、解答题（共7小题，满分69分）
18．（10分）已知，，，斜边，将绕点顺时针旋转，如图1，连接．
（1）填空：　　；
（2）如图1，连接，作，垂足为，求的长度；
（3）如图2，点，同时从点出发，在边上运动，沿路径匀速运动，沿路径匀速运动，当两点相遇时运动停止，已知点的运动速度为1.5单位秒，点的运动速度为1单位秒，设运动时间为秒，的面积为，求当为何值时取得最大值？最大值为多少？

19．（5分）孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查，得到了一组学生捐款情况的数据．如图是根据这组数据绘制的统计图，图中从左到右各长方形的高度之比为3：4：5：10：8，又知此次调查中捐款30元的学生一共16人．孔明同学调查的这组学生共有_______人；这组数据的众数是_____元，中位数是_____元；若该校有2000名学生，都进行了捐款，估计全校学生共捐款多少元？

20．（8分）如图，已知∠AOB与点M、N求作一点P，使点P到边OA、OB的距离相等，且PM=PN（保留作图痕迹，不写作法）

21．（10分）如图，BD是矩形ABCD的一条对角线．
（1）作BD的垂直平分线EF，分别交AD、BC于点E、F，垂足为点O．（要求用尺规作图，保留作图痕迹，不要求写作法）；
（2）求证：DE=BF．

22．（10分）如图，已知AB是⊙O上的点，C是⊙O上的点，点D在AB的延长线上，∠BCD=∠BAC．求证：CD是⊙O的切线；若∠D=30°，BD=2，求图中阴影部分的面积．

23．（12分）如图，建筑物BC上有一旗杆AB，从与BC相距40m的D处观测旗杆顶部A的仰角为50°，观测旗杆底部B的仰角为45°，求旗杆AB的高度．（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）

24．（14分）如图，已知直线与抛物线相交于A，B两点，且点A（1，－4）为抛物线的顶点，点B在x轴上．

（1）求抛物线的解析式；
（2）在（1）中抛物线的第二象限图象上是否存在一点P，使△POB与△POC全等？若存在，求出点P的坐标；若不存在，请说明理由；
（3）若点Q是y轴上一点，且△ABQ为直角三角形，求点Q的坐标．



参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、B
【解析】
先证明△ABD≌△EBD，从而可得AD=DE，然后先求得△AEC的面积，继而可得到△CDE的面积.
【详解】
∵BD平分∠ABC，
∴∠ABD=∠EBD，
∵AE⊥BD，
∴∠ADB=∠EDB=90°，
又∵BD=BD，
∴△ABD≌△EBD，
∴AD=ED，
∵，的面积为1，
∴S△AEC=S△ABC=，
又∵AD=ED，
∴S△CDE= S△AEC=，
故选B.
【点睛】
本题考查了全等三角形的判定，掌握等高的两个三角形的面积之比等于底边长度之比是解题的关键.
2、C
【解析】
分析：本题需要分两种情况来进行计算得出函数解析式，即当点N和点D重合之前以及点M和点B重合之前，根据题意得出函数解析式．
详解：假设当∠A=45°时，AD=2，AB=4，则MN=t，当0≤t≤2时，AM=MN=t，则S=，为二次函数；当2≤t≤4时，S=t，为一次函数，故选C．
点睛：本题主要考查的就是函数图像的实际应用问题，属于中等难度题型．解答这个问题的关键就是得出函数关系式．
3、B
【解析】
根据图象找出一次函数图象在反比例函数图象上方时对应的自变量的取值范围即可.
【详解】
观察函数图象可发现：或时，一次函数图象在反比例函数图象上方，
∴使成立的取值范围是或，
故选B．
【点睛】
本题考查了反比例函数与一次函数综合，函数与不等式，利用数形结合思想是解题的关键.
4、B
【解析】
比较这些负数的绝对值，绝对值大的反而小.
【详解】
在﹣4、﹣、﹣1、﹣这四个数中，比﹣2小的数是是﹣4和﹣.故选B.
【点睛】
本题主要考查负数大小的比较，解题的关键时负数比较大小时，绝对值大的数反而小.
5、A
【解析】
根据任何一个一次函数都可以化为一个二元一次方程，再根据两个函数交点坐标就是二元一次方程组的解可直接得到答案．
【详解】
解：∵直线y1=k1x+b1与y2=k2x+b2的交点坐标为（2，4），
∴二元一次方程组的解为
故选A.
【点睛】
本题主要考查了函数解析式与图象的关系，满足解析式的点就在函数的图象上，在函数的图象上的点，就一定满足函数解析式．函数图象交点坐标为两函数解析式组成的方程组的解．
6、B
【解析】
试题分析：根据作图方法可得点P在第二象限角平分线上，
则P点横纵坐标的和为0，即2a+b+1=0，
∴2a+b=﹣1．故选B．
7、B
【解析】
试题分析：∵每个小正方形的边长都为1，∴OA=4，∵将△AOB绕点O顺时针旋转90°得到△A′OB′，∴∠AOA′=90°，∴A点运动的路径的长为：=2π．故选B．
考点：弧长的计算；旋转的性质．
8、D
【解析】
找到从上面看所得到的图形即可，注意所有看到的棱都应表现在俯视图中．
【详解】
从上往下看，该几何体的俯视图与选项D所示视图一致．
故选D．
【点睛】
本题考查了简单组合体三视图的知识，俯视图是从物体的上面看得到的视图．
9、C
【解析】
【分析】根据相似多边形性质：对应角相等.
【详解】由已知可得：α的度数是：360〫-60〫-75〫-138〫=87〫
故选C
【点睛】本题考核知识点：相似多边形.解题关键点：理解相似多边形性质.
10、C
【解析】
先解每一个不等式，再根据结果判断数轴表示的正确方法．
【详解】
解：由不等式①，得3x＞5-2，解得x＞1，
由不等式②，得-2x≥1-5，解得x≤2，
∴数轴表示的正确方法为C．
故选C．
【点睛】
考核知识点：解不等式组.

二、填空题（共7小题，每小题3分，满分21分）
11、36°
【解析】
由正五边形的性质得出∠B=108°，AB=CB，由等腰三角形的性质和三角形内角和定理即可得出结果．
【详解】
∵五边形ABCDE是正五边形，
∴∠B=108°，AB=CB，
∴∠ACB=（180°﹣108°）÷2=36°；
故答案为36°．
12、-1
【解析】
先求出8a+6b的值，然后整体代入进行计算即可得解．
【详解】
∵4a+3b=1，
∴8a+6b=2，
8a+6b-3=2-3=-1；
故答案为：-1．
【点睛】
本题考查了代数式求值，整体思想的利用是解题的关键．
13、35
【解析】
分析：根据捐款10元的人数占总人数25%可得捐款总人数，将总人数减去其余各组人数可得答案．
详解：根据题意可知,本年级捐款捐款的同学一共有20÷25%=80(人)，
则本次捐款20元的有：80−(20+10+15)=35(人)，
故答案为：35.
点睛：本题考查了条形统计图.计算出捐款总人数是解决问题的关键.
14、
【解析】
设AC=x,则AB=2x,根据面积公式得S△ABC=2x ,由余弦定理求得 cosC代入化简S△ABC= ,由三角形三边关系求得 ,由二次函数的性质求得S△ABC取得最大值.
【详解】
设AC=x,则AB=2x,根据面积公式得:c= =2x.由余弦定理可得: ,
∴S△ABC=2x=2x=
由三角形三边关系有 ,解得,
故当时, 取得最大值,
故答案为: .
【点睛】
本题主要考查了余弦定理和面积公式在解三角形中的应用,考查了二次函数的性质,考查了计算能力,当涉及最值问题时,可考虑用函数的单调性和定义域等问题,属于中档题.
15、x（x+2）（x﹣2）．
【解析】
试题分析：==x（x+2）（x﹣2）．故答案为x（x+2）（x﹣2）．
考点：提公因式法与公式法的综合运用；因式分解．
16、10°
【解析】
根据线段的垂直平分线得出AD=BD，AE=CE，推出∠B=∠BAD，∠C=∠CAE，求出∠BAD+∠CAE的度数即可得到答案．
【详解】
∵点D、E分别是AB、AC边的垂直平分线与BC的交点，
∴AD=BD，AE=CE，
∴∠B=∠BAD，∠C=∠CAE，
∵∠B=40°，∠C=45°，
∴∠B+∠C=85°，
∴∠BAD+∠CAE=85°，
∴∠DAE=∠BAC-（∠BAD+∠CAE）=180°-85°-85°=10°，
故答案为10°
【点睛】
本题主要考查对等腰三角形的性质，三角形的内角和定理，线段的垂直平分线的性质等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键．
17、（a+1）1．
【解析】
原式提取公因式，计算即可得到结果．
【详解】
原式=（a+1）[1+a+a（a+1）+a（a+1）2+…+a（a+1）98]，
=（a+1）2[1+a+a（a+1）+a（a+1）2+…+a（a+1）97]，
=（a+1）3[1+a+a（a+1）+a（a+1）2+…+a（a+1）96]，
=…，
=（a+1）1．
故答案是：（a+1）1．
【点睛】
考查了因式分解-提公因式法，熟练掌握提取公因式的方法是解本题的关键．

三、解答题（共7小题，满分69分）
18、（1）1；（2）；（3）x时，y有最大值，最大值．
【解析】
（1）只要证明△OBC是等边三角形即可；
（2）求出△AOC的面积，利用三角形的面积公式计算即可；
（3）分三种情形讨论求解即可解决问题：①当0＜x时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E．②当x≤4时，M在BC上运动，N在OB上运动．③当4＜x≤4.8时，M、N都在BC上运动，作OG⊥BC于G．
【详解】
（1）由旋转性质可知：OB＝OC，∠BOC＝1°，
∴△OBC是等边三角形，
∴∠OBC＝1°．
故答案为1．
（2）如图1中．

∵OB＝4，∠ABO＝30°，
∴OAOB＝2，ABOA＝2，
∴S△AOC•OA•AB2×2．
∵△BOC是等边三角形，
∴∠OBC＝1°，∠ABC＝∠ABO+∠OBC＝90°，
∴AC，
∴OP．
（3）①当0＜x时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E．

则NE＝ON•sin1°x，
∴S△OMN•OM•NE1.5xx，
∴yx2，
∴x时，y有最大值，最大值．
②当x≤4时，M在BC上运动，N在OB上运动．

作MH⊥OB于H．
则BM＝8﹣1.5x，MH＝BM•sin1°（8﹣1.5x），
∴yON×MHx2+2x．
当x时，y取最大值，y，
③当4＜x≤4.8时，M、N都在BC上运动，

作OG⊥BC于G．MN＝12﹣2.5x，OG＝AB＝2，
∴y•MN•OG＝12x，
当x＝4时，y有最大值，最大值＝2．
综上所述：y有最大值，最大值为．
【点睛】
本题考查几何变换综合题、30度的直角三角形的性质、等边三角形的判定和性质、三角形的面积等知识，解题的关键是学会用分类讨论的思想思考问题．
19、（1）60；（2）20，20；（3）38000
【解析】
（1）利用从左到右各长方形高度之比为3：4：5：10：8，可设捐5元、10元、15元、20元和30元的人数分别为3x、4x、5x、10x、8x，则根据题意得8x=1，解得x=2，然后计算3x+4x+5x++10x+8x即可；
（2）先确定各组的人数，然后根据中位数和众数的定义求解；
（3）先计算出样本的加权平均数，然后利用样本平均数估计总体，用2000乘以样本平均数即可．
【详解】
（1）设捐5元、10元、15元、20元和30元的人数分别为3x、4x、5x、10x、8x，则8x=1，解得：x=2，∴3x+4x+5x+10x+8x=30x=30×2=60（人）；
（2）捐5元、10元、15元、20元和30元的人数分别为6，8，10，20，1．
∵20出现次数最多，∴众数为20元；
∵共有60个数据，第30个和第31个数据落在第四组内，∴中位数为20元；
（3）2000=38000（元），∴估算全校学生共捐款38000元．
【点睛】
本题考查了条形统计图：条形统计图是用线段长度表示数据，根据数量的多少画成长短不同的矩形直条，然后按顺序把这些直条排列起来．也考查了样本估计总体、中位数与众数．
20、见解析
【解析】
作∠AOB的角平分线和线段MN的垂直平分线，它们的交点即是要求作的点P.
【详解】
解：①作∠AOB的平分线OE，②作线段MN的垂直平分线GH，GH交OE于点P．
点P即为所求．

【点睛】
本题考查了角平分线和线段垂直平分线的尺规作法，熟练掌握角平分线和线段垂直平分线的的作图步骤是解答本题的关键.
21、（1）作图见解析；（2）证明见解析；
【解析】
（1）分别以B、D为圆心，以大于BD的长为半径四弧交于两点，过两点作直线即可得到线段BD的垂直平分线；
（2）利用垂直平分线证得△DEO≌△BFO即可证得结论．
【详解】
解：（1）如图：

（2）∵四边形ABCD为矩形，
∴AD∥BC，
∴∠ADB=∠CBD，
∵EF垂直平分线段BD，
∴BO=DO，
在△DEO和三角形BFO中，
，
∴△DEO≌△BFO（ASA），
∴DE=BF．
考点：1．作图—基本作图；2．线段垂直平分线的性质；3．矩形的性质．
22、（1）证明见解析；（2）阴影部分面积为
【解析】
【分析】（1）连接OC，易证∠BCD=∠OCA，由于AB是直径，所以∠ACB=90°，所以∠OCA+OCB=∠BCD+∠OCB=90°，CD是⊙O的切线；
（2）设⊙O的半径为r，AB=2r，由于∠D=30°，∠OCD=90°，所以可求出r=2，∠AOC=120°，BC=2，由勾股定理可知：AC=2，分别计算△OAC的面积以及扇形OAC的面积即可求出阴影部分面积.
【详解】（1）如图，连接OC，
∵OA=OC，
∴∠BAC=∠OCA，
∵∠BCD=∠BAC，
∴∠BCD=∠OCA，
∵AB是直径，
∴∠ACB=90°，
∴∠OCA+OCB=∠BCD+∠OCB=90°
∴∠OCD=90°
∵OC是半径，
∴CD是⊙O的切线
（2）设⊙O的半径为r，
∴AB=2r，
∵∠D=30°，∠OCD=90°，
∴OD=2r，∠COB=60°
∴r+2=2r，
∴r=2，∠AOC=120°
∴BC=2，
∴由勾股定理可知：AC=2，
易求S△AOC=×2×1=
S扇形OAC=，
∴阴影部分面积为.

【点睛】本题考查圆的综合问题，涉及圆的切线判定，勾股定理，含30度的直角三角形的性质，等边三角形的性质等知识，熟练掌握和灵活运用相关知识是解题的关键.
23、7.6 m．
【解析】
利用CD及正切函数的定义求得BC，AC长，把这两条线段相减即为AB长
【详解】
解：由题意，∠BDC＝45°，∠ADC＝50°，∠ACD＝90°，CD＝40 m．
∵在Rt△BDC中，tan∠BDC＝．
∴BC＝CD＝40 m．
∵在Rt△ADC中，tan∠ADC＝．
∴．
∴AB≈7.6（m）．
答：旗杆AB的高度约为7.6 m．
【点睛】
此题主要考查了解直角三角形的应用，正确应用锐角三角函数关系是解题关键．
24、解：（1）；（2）存在，P（，）；（1）Q点坐标为（0，-）或（0，）或（0，－1）或（0，－1）.
【解析】
（1）已知点A坐标可确定直线AB的解析式，进一步能求出点B的坐标．点A是抛物线的顶点，那么可以将抛物线的解析式设为顶点式，再代入点B的坐标，依据待定系数法可解.
（2）首先由抛物线的解析式求出点C的坐标，在△POB和△POC中，已知的条件是公共边OP，若OB与OC不相等，那么这两个三角形不能构成全等三角形；若OB等于OC，那么还要满足的条件为：∠POC=∠POB，各自去掉一个直角后容易发现，点P正好在第二象限的角平分线上，联立直线y=-x与抛物线的解析式，直接求交点坐标即可，同时还要注意点P在第二象限的限定条件.
（1）分别以A、B、Q为直角顶点，分类进行讨论，找出相关的相似三角形，依据对应线段成比例进行求解即可.
【详解】
解：（1）把A（1，﹣4）代入y＝kx﹣6，得k＝2，
∴y＝2x﹣6，
令y＝0，解得：x＝1，
∴B的坐标是（1，0）．
∵A为顶点，
∴设抛物线的解析为y＝a（x﹣1）2﹣4，
把B（1，0）代入得：4a﹣4＝0，
解得a＝1，
∴y＝（x﹣1）2﹣4＝x2﹣2x﹣1．
（2）存在．
∵OB＝OC＝1，OP＝OP，
∴当∠POB＝∠POC时，△POB≌△POC，
此时PO平分第二象限，即PO的解析式为y＝﹣x．
设P（m，﹣m），则﹣m＝m2﹣2m﹣1，解得m＝（m＝＞0，舍），
∴P（，）．
（1）①如图，当∠Q1AB＝90°时，△DAQ1∽△DOB，
∴，即=，∴DQ1＝，
∴OQ1＝，即Q1（0，-）；
②如图，当∠Q2BA＝90°时，△BOQ2∽△DOB，
∴，即，
∴OQ2＝，即Q2（0，）；
③如图，当∠AQ1B＝90°时，作AE⊥y轴于E，

则△BOQ1∽△Q1EA，
∴，即
∴OQ12﹣4OQ1+1＝0，∴OQ1＝1或1，
即Q1（0，﹣1），Q4（0，﹣1）．
综上，Q点坐标为（0，-）或（0，）或（0，﹣1）或（0，﹣1）．