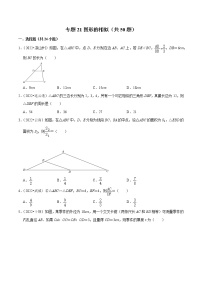
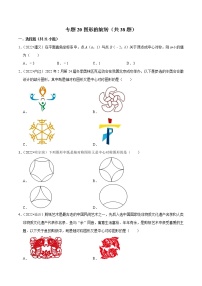
所属成套资源:2022年中考数学真题考点分类汇编(全国通用)【解析版】汇总
专题07分式方程-备战2023年中考数学必刷真题考点分类专练(全国通用)【解析版】
展开
这是一份专题07分式方程-备战2023年中考数学必刷真题考点分类专练(全国通用)【解析版】,文件包含专题07分式方程-备战2023年中考数学必刷真题考点分类专练全国通用解析版docx、专题07分式方程-备战2023年中考数学必刷真题考点分类专练全国通用原卷版docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
专题07分式方程一.选择题(共7小题)1.(2022•德阳)如果关于x的方程1的解是正数,那么m的取值范围是( )A.m>﹣1 B.m>﹣1且m≠0 C.m<﹣1 D.m<﹣1且m≠﹣2【分析】先去分母将分式方程化成整式方程,再求出方程的解x=﹣1﹣m,利用x>0和x≠1得出不等式组,解不等式组即可求出m的范围.【解析】两边同时乘(x﹣1)得,2x+m=x﹣1,解得:x=﹣1﹣m,又∵方程的解是正数,且x≠1,∴,即,解得:,∴m的取值范围为:m<﹣1且m≠﹣2.故答案为:D.【点评】本题主要考查了分式方程的解,一元一次不等式,正确求得分式方程的解并考虑产生增根的情形是解题的关键.2.(2022•遂宁)若关于x的方程无解,则m的值为( )A.0 B.4或6 C.6 D.0或4【分析】解分式方程可得(4﹣m)x=﹣2,根据题意可知,4﹣m=0或x,求出m的值即可.【解析】,2(2x+1)=mx,4x+2=mx,(4﹣m)x=﹣2,∵方程无解,∴4﹣m=0或x,∴m=4或m=0,故选:D.【点评】本题考查分式方程的解法,熟练掌握分式方程的解法,分式方程无解的条件是解题的关键.3.(2022•广元)某药店在今年3月份购进了一批口罩,这批口罩包括一次性医用外科口罩和N95口罩,且两种口罩的只数相同,其中一次性医用外科口罩花费1600元,N95口罩花费9600元.已知一次性医用外科口罩的单价比N95口罩的单价少10元,那么一次性医用外科口罩的单价为多少元?设一次性医用外科口罩单价为x元,则列方程正确的是( )A. B. C. D.10【分析】设该药店购进的一次性医用外科口罩的单价是x元,则购进N95口罩的单价是(x+10)元,利用数量=总价÷单价,结合购进两种口罩的只数相同,即可得出关于x的分式方程.【解析】设该药店购进的一次性医用外科口罩的单价是x元,则购进N95口罩的单价是(x+10)元,依题意得:,故选:B.【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.4.(2022•云南)某地开展建设绿色家园活动,活动期间,计划每天种植相同数量的树木.该活动开始后,实际每天比原计划每天多植树50棵,实际植树400棵所需时间与原计划植树300棵所需时间相同.设实际每天植树x棵,则下列方程正确的是( )A. B. C. D.【分析】根据实际植树400棵所需时间与原计划植树300棵所需时间相同,可以列出相应的分式方程,本题得以解决.【解析】由题意可得,,故选:B.【点评】本题考查由实际问题抽象出分式方程,解答本题的关键是明确题意,找出等量关系,列出相应的方程.5.(2022•丽水)某校购买了一批篮球和足球.已知购买足球的数量是篮球的2倍,购买足球用了5000元,购买篮球用了4000元,篮球单价比足球贵30元.根据题意可列方程30,则方程中x表示( )A.足球的单价 B.篮球的单价 C.足球的数量 D.篮球的数量【分析】设篮球的数量为x个,足球的数量是2x个,列出分式方程解答即可.【解析】设篮球的数量为x个,足球的数量是2x个.根据题意可得:30,故选:D.【点评】此题主要考查了由实际问题抽象出分式方程,得到相应的关系式是解决本题的关键.6.(2022•重庆)关于x的分式方程1的解为正数,且关于y的不等式组的解集为y≥5,则所有满足条件的整数a的值之和是( )A.13 B.15 C.18 D.20【分析】解分式方程得得出x=a﹣2,结合题意及分式方程的意义求出a>2且a≠5,解不等式组得出,结合题意得出a≤7,进而得出2<a≤7且a≠5,继而得出所有满足条件的整数a的值之和,即可得出答案.【解析】解分式方程得:x=a﹣2,∵x>0且x≠3,∴a﹣2>0且a﹣2≠3,∴a>2且a≠5,解不等式组得:,∵不等式组的解集为y≥5,∴5,∴a<7,∴2<a<7且a≠5,∴所有满足条件的整数a的值之和为3+4+6=13,故选:A.【点评】本题考查了分式方程的解,解一元一次不等式组,解一元一次不等式,一元一次不等式的整数解,正确求解分式方程,一元一次不等式组,一元一次不等式是解决问题的关键.7.(2022•重庆)若关于x的一元一次不等式组的解集为x≤﹣2,且关于y的分式方程2的解是负整数,则所有满足条件的整数a的值之和是( )A.﹣26 B.﹣24 C.﹣15 D.﹣13【分析】解不等式组得出,结合题意得出a>﹣11,解分式方程得出y,结合题意得出a=﹣8或﹣5,进而得出所有满足条件的整数a的值之和是﹣8﹣5=﹣13,即可得出答案.【解析】解不等式组得:,∵不等式组的解集为x≤﹣2,∴2,∴a>﹣11,解分式方程2得:y,∵y是负整数且y≠﹣1,∴是负整数且1,∴a=﹣8或﹣5,∴所有满足条件的整数a的值之和是﹣8﹣5=﹣13,故选:D.【点评】本题考查了分式方程的解,解一元一次不等式组,正确求解分式方程和一元一次不等式组是解决问题的关键.二.填空题(共6小题)8.(2022•宁波)定义一种新运算:对于任意的非零实数a,b,a⊗b.若(x+1)⊗x,则x的值为 .【分析】根据新定义列出分式方程,解方程即可得出答案.【解析】根据题意得:,化为整式方程得:x+x+1=(2x+1)(x+1),解得:x,检验:当x时,x(x+1)≠0,∴原方程的解为:x.故答案为:.【点评】本题考查了解分式方程,新定义,根据新定义列出分式方程是解题的关键.9.(2022•江西)甲、乙两人在社区进行核酸采样,甲每小时比乙每小时多采样10人,甲采样160人所用时间与乙采样140人所用时间相等,甲、乙两人每小时分别采样多少人?设甲每小时采样x人,则可列分式方程为 .【分析】由实际问题找到合适的等量关系即可抽象出分式方程.【解析】设甲每小时采样x人,则乙每小时采样(x﹣10)人,根据题意得:.故答案为:.【点评】本题考查由实际问题抽象出分式方程,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.10.(2022•金华)若分式的值为2,则x的值是 4 .【分析】依据题意列出分式方程,解分式方程即可求得结论.【解析】由题意得:2,去分母得:2=2(x﹣3),去括号得:2x﹣6=2,移项,合并同类项得:2x=8,∴x=4.经检验,x=4是原方程的根,∴x=4.故答案为:4.【点评】本题主要考查了解分式方程,解分式方程需要验根,这是容易丢掉的步骤.11.(2022•泸州)若方程1的解使关于x的不等式(2﹣a)x﹣3>0成立,则实数a的取值范围是 a<﹣1 .【分析】先解分式方程,再将x代入不等式中即可求解.【解析】1,,0,解得:x=1,∵x﹣2≠0,2﹣x≠0,∴x=1是分式方程的解,将x=1代入不等式(2﹣a)x﹣3>0,得:2﹣a﹣3>0,解得:a<﹣1,∴实数a的取值范围是a<﹣1,故答案为:a<﹣1.【点评】本题考查分式方程的解,不等式的解集,解题的关键是正确求出分式方程的解,要注意分母不能为0.12.(2022•成都)分式方程1的解为 x=3 .【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解析】去分母得:3﹣x﹣1=x﹣4,解得:x=3,经检验x=3是分式方程的解,故答案为:x=3【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.13.(2022•邵阳)分式方程0的解是 x=﹣3 .【分析】依据解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.【解析】去分母,得:5x﹣3(x﹣2)=0,整理,得:2x+6=0,解得:x=﹣3,经检验:x=﹣3是原分式方程的解,故答案为:x=﹣3.【点评】本题主要考查解分式方程能力,熟练掌握解分式方程的步骤是关键.三.解答题(共10小题)14.(2022•苏州)解方程:1.【分析】先两边同乘以x(x+1)化为整式方程:x2+3(x+1)=x(x+1),解整式方程得x,再检验即可得答案.【解析】方程两边同乘以x(x+1)得:x2+3(x+1)=x(x+1),解整式方程得:x,经检验,x是原方程的解,∴原方程的解为x.【点评】本题考查解分式方程,解题的关键是掌握解分式方程的一般步骤,特别注意解分式方程必须检验.15.(2022•眉山)解方程:.【分析】按照解分式方程的步骤,进行计算即可解答.【解析】,方程两边同乘(x﹣1)(2x+1)得:2x+1=3(x﹣1),解这个整式方程得:x=4,检验:当x=4时,(x﹣1)(2x+1)≠0,∴x=4是原方程的解.【点评】本题考查了解分式方程,熟记解分式方程的步骤是解题的关键,需要特别注意解分式方程需要检验.16.(2022•嘉兴)(1)计算:(1)0.(2)解方程:1.【分析】(1)分别利用0指数幂、算术平方根的定义化简,然后加减求解;(2)首先去分母化分式方程为整式方程,然后解整式方程,最后验根.【解析】(1)原式=1﹣2=﹣1;(2)去分母得x﹣3=2x﹣1,∴﹣x=3﹣1,∴x=﹣2,经检验x=﹣2是分式方程的解,∴原方程的解为:x=﹣2.【点评】本题分别考查了实数的运算和解分式方程,实数的运算主要利用0指数幂及算术平方根的定义,解分式方程的基本方法时去分母.17.(2022•宿迁)解方程:.【分析】根据解分式方程的步骤,先去分母化为整式方程,再求出方程的解,最后进行检验即可.【解析】1,2x=x﹣2+1,x=﹣1,经检验x=﹣1是原方程的解,则原方程的解是x=﹣1.【点评】此题考查了解分式方程,用到的知识点是解分式方程的步骤:去分母化整式方程,解整式方程,最后要把整式方程的解代入最简公分母进行检验.18.(2022•常德)小强的爸爸平常开车从家中到小强奶奶家,匀速行驶需要4小时.某天,他们以平常的速度行驶了的路程时遇到了暴雨,立即将车速减少了20千米/小时,到达奶奶家时共用了5小时,问小强家到他奶奶家的距离是多少千米?【分析】设平常的速度是x千米/小时,根据“到达奶奶家时共用了5小时”列分式方程,求解即可.【解析】设平常的速度是x千米/小时,根据题意,得,解得x=60,经检验,x=60是原方程的根,4×60=240(千米),答:小强家到他奶奶家的距离是240千米.【点评】本题考查了分式方程的应用,理解题意并根据题意建立等量关系是解题的关键.19.(2022•乐山)第十四届四川省运动会定于2022年8月8日在乐山市举办.为保证省运会期间各场馆用电设施的正常运行,市供电局为此进行了电力抢修演练.现抽调区县电力维修工人到20千米远的市体育馆进行电力抢修.维修工人骑摩托车先行出发,10分钟后,抢修车装载完所需材料再出发,结果他们同时到达体育馆.已知抢修车是摩托车速度的1.5倍,求摩托车的速度.【分析】设摩托车的速度为x千米/小时,则抢修车的速度为1.5x千米/小时,根据时间=路程÷速度结合骑摩托车的维修工人比乘抢修车的工人多用10分钟到达,即可得出关于x的分式方程,解之经检验后即可得出结论.【解析】设摩托车的速度为x千米/小时,则抢修车的速度为1.5x千米/小时,依题意,得:,解得:x=10,经检验,x=10是原方程的解,且符合题意.答:摩托车的速度为10千米/小时.【点评】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.20.(2022•扬州)某中学为准备十四岁青春仪式,原计划由八年级(1)班的4个小组制作360面彩旗,后因1个小组另有任务,其余3个小组的每名学生要比原计划多做3面彩旗才能完成任务.如果这4个小组的人数相等,那么每个小组有学生多少名?【分析】设每个小组有学生x名,由题意得:,解分式方程并检验后即可得出答案.【解析】设每个小组有学生x名,由题意得:,解得:x=10,当x=10时,12x≠0,∴x=10是分式方程的根,答:每个小组有学生10名.【点评】本题考查了分式方程的应用,根据题意列出分式方程是解决问题的关键.21.(2022•达州)某商场进货员预测一种应季T恤衫能畅销市场,就用4000元购进一批这种T恤衫,面市后果然供不应求.商场又用8800元购进了第二批这种T恤衫,所购数量是第一批购进量的2倍,但每件的进价贵了4元.(1)该商场购进第一批、第二批T恤衫每件的进价分别是多少元?(2)如果两批T恤衫按相同的标价销售,最后缺码的40件T恤衫按七折优惠售出,要使两批T恤衫全部售完后利润率不低于80%(不考虑其他因素),那么每件T恤衫的标价至少是多少元?【分析】(1)设该商场购进第一批、第二批T恤衫每件的进价分别是x元和(x+4)元,根据所购数量是第一批购进量的2倍列出方程解答即可;(2)设每件T恤衫的标价至少是y元,根据题意列出不等式解答即可.【解答】(1)解:设该商场购进第一批、第二批T恤衫每件的进价分别是x元和(x+4)元,根据题意可得:,解得:x=40,经检验x=40是方程的解,x+4=40+4=44,答:该商场购进第一批、第二批T恤衫每件的进价分别是40元和44元;(2)解:(件),设每件T恤衫的标价至少是y元,根据题意可得:(300﹣40)y+40×0.7y≥(4000+8800)×(1+80%),解得:y≥80,答:每件T恤衫的标价至少是80元.【点评】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.22.(2022•重庆)为保障蔬菜基地种植用水,需要修建灌溉水渠.(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工人员,每天比原来多修建20米,再施工2天完成任务,求甲施工队增加人员后每天修建灌溉水渠多少米?(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建360米后,通过技术更新,每天比原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好相同.求乙施工队原来每天修建灌溉水渠多少米?【分析】(1)根据题意可知:甲原来工作5天的工作量+后来2天的工作量=600,可以列出相应的方程,然后求解即可;(2)根据题意可知:甲、乙施工的长度都是900米,再根据题意可知,两个工程队施工天数相同,即可列出相应的分式方程,然后求解即可,注意分式方程要检验.【解析】(1)设甲施工队增加人员后每天修建灌溉水渠x米,则原计划每天施工(x﹣20)米,由题意可得:5(x﹣20)+2x=600,解得x=100,答:甲施工队增加人员后每天修建灌溉水渠100米;(2)设乙施工队原来每天修建灌溉水渠m米,则技术更新后每天修建水渠m(1+20%)=1.2m米,由题意可得:,解得m=90,经检验,m=90是原分式方程的解,答:乙施工队原来每天修建灌溉水渠90米.【点评】本题考查一元一次方程的应用、分式方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的分式方程和一元一次方程.23.(2022•自贡)学校师生去距学校45千米的吴玉章故居开展研学旅行活动,骑行爱好者张老师骑自行车先行2小时后,其余师生乘汽车出发,结果同时到达.已知汽车速度是自行车速度的3倍,求张老师骑车的速度.【分析】根据题意可知:张老师骑车用的时间﹣汽车用的时间=2,即可列出相应的分式方程,然后求解即可,注意分式方程要检验.【解析】设张老师骑车的速度为x千米/小时,则汽车的速度为3x千米/小时,由题意可得:2,解得x=15,经检验,x=15是原分式方程的解,答:张老师骑车的速度是15千米/小时.【点评】本题考查分式方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的分式方程.
相关试卷
这是一份2022年中考数学必刷真题考点分类专练(全国通用) 专题07分式方程【原卷版+解析】,共16页。
这是一份初中数学中考复习 专题07分式方程-备战2023年中考数学必刷真题考点分类专练(全国通用)【原卷版】,共4页。
这是一份初中数学中考复习 专题07分式方程-备战2023年中考数学必刷真题考点分类专练(全国通用)【解析版】,共13页。