高中数学湘教版（2019）选择性必修 第二册1.1 导数概念及其意义授课ppt课件

这是一份高中数学湘教版（2019）选择性必修 第二册1.1 导数概念及其意义授课ppt课件，共28页。PPT课件主要包含了一创设问题情境，二聚焦问题难点，x2－x1，y2－y1，气球的平均膨胀率为，x3x4，课堂小结，割线斜率，山坡陡峭程度，函数的平均变化率等内容，欢迎下载使用。

在爬山过程中，我们都有这样的感觉：当山坡平缓时，步履轻盈；当山坡陡峭时，气喘吁吁．怎样用数学来刻画山坡的平缓与陡峭程度呢？
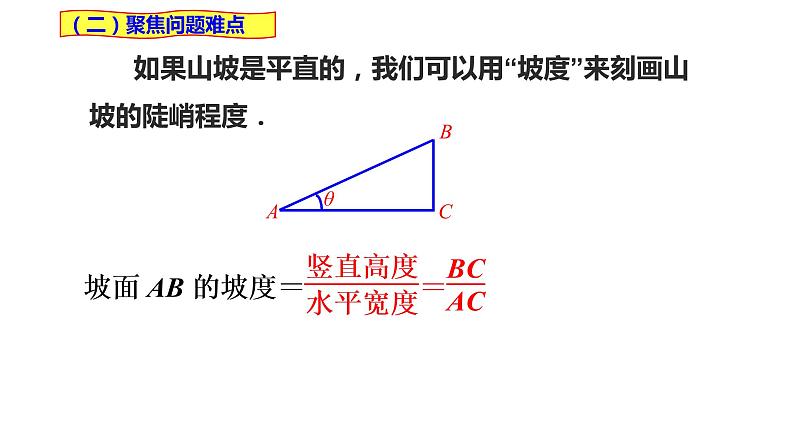
如果山坡是平直的，我们可以用“坡度”来刻画山坡的陡峭程度．
例1 设数轴上的动点P在任何时刻t的位置均可用函数f(t)=0.5t+1表示，求该点P在时间段[a，b] 内的平均速度v[a，b].
所以点P在时间段 [a，b]内的平均速度为0.5.
由例1可知，该动点在任何一个时间段[a，b]内的平均速度都等于0.5，是常数. 由此可见，该动点做匀速运动，且在任何时刻的速度都是0.5.
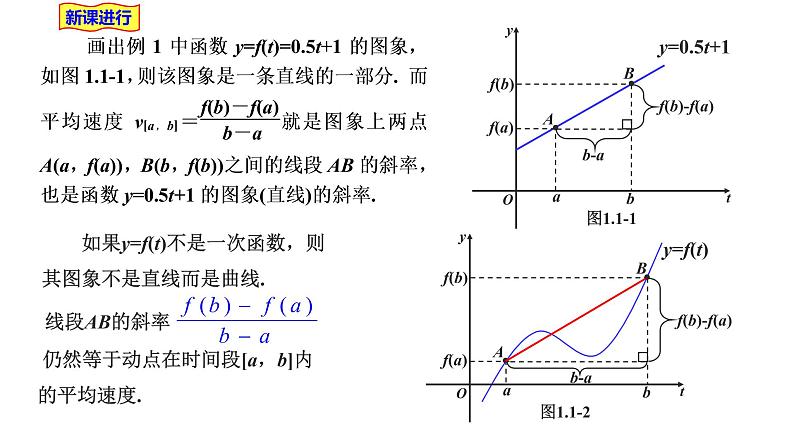
如果y=f(t)不是一次函数，则其图象不是直线而是曲线.
线段AB的斜率 仍然等于动点在时间段[a，b]内的平均速度.
解：物体在时间段[1，3]内的平均速度为
例2 某物体做自由落体运动，其运动方程为 ，其中t为下落的时间(单位：s)，g为重力加速度，大小为9.8 m/s2 . 求它在时间段[1，3]内的平均速度.
函数的平均变化率就是曲线的割线的斜率，这也是函数平均变化率的几何意义.
例4 充满气的气球近似为球体. 在给气球充气时, 我们都知道,开始充气时气球膨胀较快, 随后膨胀速度逐渐缓慢下来，从数学的角度, 如何描述这种现象呢?
气球的体积V(单位:L)与半径r (单位:dm)之间的函数关系是
若将半径 r 表示为体积V的函数, 那么
当空气容量V从0L增加到1L , 气球半径增加了
当空气容量V从1L增加到2 L , 气球半径增加了
随着气球体积逐渐变大,它的平均膨胀率逐渐变小
例5 已知函数f(x)=3x+2，g(x)=x2分别计算它们在区间[-2，-1]，[1，5]上的平均变化率.
解：函数f(x)=3x+2在[-2，-1]上的平均变化率为
函数f(x)=3x+2在[1，5]上的平均变化率为
解：函数g(x)=x2在[-2，-1]上的平均变化率为
函数g(x)=x2在[1，5]上的平均变化率为
7．如果过点P(－2，m)和Q(m,4)的直线的斜率等于1，那么m的值为 (　　)A．1　 B．4　　C．1或3　 D．1或4
8．已知函数f(x)＝2x2－4的图像上两点A，B，且xA＝1，xB＝1.1，则函数f(x)从A点到B点的平均变化率为(　　)A．4　 B．4x　　 C．4.2　 D．4.02
KE TANG XIAO JIE