数学人教A版 (2019)1.2 集合间的基本关系背景图课件ppt

这是一份数学人教A版 (2019)1.2 集合间的基本关系背景图课件ppt，共15页。PPT课件主要包含了A⊆B或B⊇A，真子集，常用结论，abc，3AB，补充例题等内容，欢迎下载使用。
我们知道，两个实数之间有相等关系、大小关系，如5＝5，5＜7，5＞3，等等，类比实数之间的关系，两个集合之间是否也有类似的关系？下面我们通过具体例子探究这个问题.
探究 观察下面几个例子，类比实数之间的相等关系、大小关系，你能发现下面两个集合之间的关系吗？（1）A={1, 2, 3}，B={1, 2, 3, 4, 5}；（2）C为立德中学高一(2)班全体女生组成的集合，D为这个班的全体学生组成的集合；（3）E={x|x是两条边长相等的三角形}，F={x|x是等腰三角形}.
可以发现，在(1)中，集合A的任何一个元素都是集合B的元素. 这时我们说集合A包含于集合B，或集合B包含集合A. (2) (3)中的两个集合之间也有这种关系.
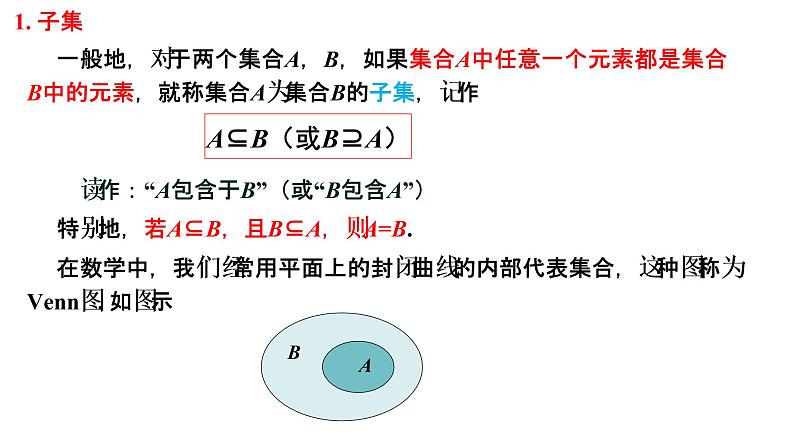
一般地，对于两个集合A，B，如果集合A中任意一个元素都是集合B中的元素，就称集合A为集合B的子集，记作
读作：“A包含于B”（或“B包含A”）
在数学中，我们经常用平面上的封闭曲线的内部代表集合，这种图称为Venn图. 如图示
特别地，若A⊆B，且B⊆A，则A=B.
如果集合A⊆B，但存在元素x∈B，且xA，就称集合A是集合B的真子集，记作
读作：“A真包含于B”（或“B真包含A”）
思考 方程x2+1=0的实数根组成集合是什么？它的元素有哪些？
我们知道，方程x2+1=0是没有实数根，所以方程x2+1=0的实数根组成的集合中没有元素.
一般地，我们把不含任何元素的集合叫做空集，记为∅，并规定：空集是任何集合A的子集. 即∅⊆A. 是任何非空集合的真子集.
思考 包含关系{a}⊆A与属于关系a∈A有什么区别？试结合实例作出解释？
包含关系是集合与集合之间的关系，用“⊆”表示；
属于关系是元素与集合之间的关系，用“∈”表示.
二者切不可混淆，用符号之前要搞清楚是元素与集合还是集合与集合的关系.
由集合之间的基本关系，可以得到以下结论：
(1)任何一个集合都是它本身的子集，即A⊆A；
(2)对于集合A, B, C，如果A⊆B，且B⊆C，那么A⊆C；
(3)对于两个集合A, B，如果A⊆B，且B⊆A，那么A=B；
(4)空集∅是任何集合的子集，是任何非空集合的真子集.
例1 写出集合{a,b}的所有子集，并指出哪些是它的真子集.
解：集合{a, b}的所有子集为∅，{a}，{b}，{a, b}. 真子集为∅，{a}，{b}.
P8练习1 写出集合{a, b, c}的所有子集，并指出哪些是它的真子集.
思考 如果一个集合中有n个元素，则其子集有多少个？真子集有多少个？
如果一个集合中有n个元素，则其子集有2n个. 真子集有2n-1个.
例2 判断下列各题中集合A是否为集合B的子集，并说明理由：（1）A={1, 2, 3}，B={x|x是8的约数}；（2）A={x|x是长方形}，B={x|x是两条对角线相等的平行四边形}.
解：(1) 因为3不是8的约数，所以集合A不是集合B的子集. (2) 因为若x是长方形，则x一定是两条对角线相等的平行四边形，所以集合A是集合B的子集.
P8练习3 判断下列两个集合之间的关系：（1）A={x|x