北师大版八年级下册3 公式法图文ppt课件

这是一份北师大版八年级下册3 公式法图文ppt课件，共20页。PPT课件主要包含了知识回顾，因式分解，提公因式法，平方差公式，同学们拼出图形为，获取新知，a+b2，a2+2ab+b2，a2－2ab+b2，观察这两个式子等内容，欢迎下载使用。

把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法？
a2-b2=(a + b)(a - b)
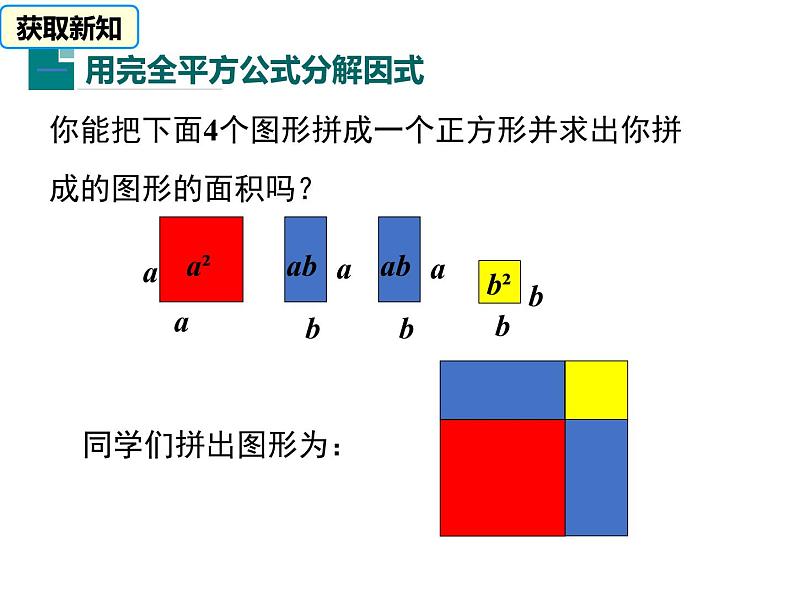
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗？
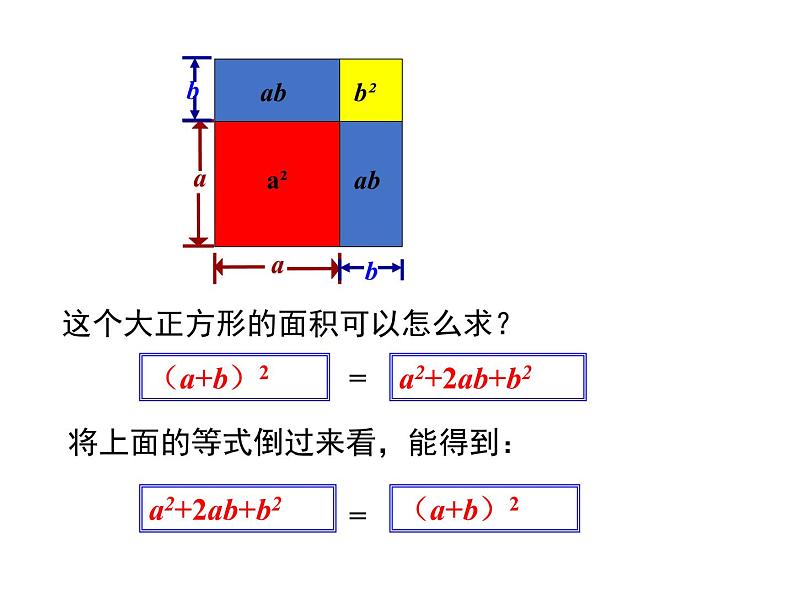
这个大正方形的面积可以怎么求？
将上面的等式倒过来看，能得到：
我们把a²+2ab+b²和a²－2ab+b²这样的式子叫作完全平方式.
（1）每个多项式有几项？
（3）中间项和第一，第三项什么关系？
（2）每个多项式第一项和第三项有什么特征？
这两项都是数或式的平方，并且符号相同
是第一项和第三项底数的积的±2倍
完全平方式的特点： 1.必须是三项式（或可以看成三项的）； 2.有两个同号的数或式的平方； 3.中间有两底数之积的±2倍.
简记口诀： 首平方，尾平方，首尾两倍在中央.
凡具备这些特点的三项式，就是完全平方式，将它写成完全平方形式，便实现了因式分解.
两个数的平方和加上(或减去)这两个数的积的2倍，等于这两个数的和(或差)的平方.
利用公式把某些具有特殊形式（如平方差式，完全平方式等）的多项式分解因式，这种分解因式的方法叫做公式法.
3.a²+4ab+4b²=( )²+2· ( ) ·( )+( )²=( )²
2.m²-6m+9=( )² - 2· ( ) ·( )+( )² =( )²
1. x²+4x+4= ( )² +2·( )·( )+( )² =( )²
对照 a²±2ab+b²=(a±b)²，填空：
例1 把下列完全平方式因式分解：（1）x2+14x+49； （2） (m+n)2 -6 (m+n)+9.
解：(1)x2＋14x＋49 ＝ x2＋ 2·x·7 ＋72 ＝ (x＋7) 2
(2)(m＋n)2－6(m＋n)＋9＝(m＋n)2－2·(m＋n)·3＋32＝(m＋n－3)2.
方法总结：公式中的a、b无论表示数、单项式、还是多项式，只要被分解的多项式能转化成完全平方的形式，就能用完全平方公式因式分解.
例2 把下列各式分解因式： (1)3ax2+6axy+3ay2 ；(2)－x2－4y2＋4xy.
解: (1)原式=3a（x2+2xy+y2） =3a（x+y）2；
分析：(1)中有公因式3a,应先提出公因式，再进一步分解因式；
(2)当首项的二次项系数为负数时，一般应先提出“－”号或整个负数
(2)－x2－4y2＋4xy＝ －(x2＋4y2－4xy)＝ －(x2－4xy＋4y2)＝－[x2－2·x·2y＋(2y)2]＝ －(x－2y)2.
方法总结：分解因式前应先分析多项式的特点，一般先提公因式，再套用公式，平方项为负的先提出负号．注意分解因式必须进行到每一个多项式都不能再分解因式为止．
1、下列各式是不是完全平方式？ （1）a2－4a+4; （2）1+4a²; （3）4b2+4b-1; （4）a2+ab+b2; （5）x2+x+0.25.
（2）因为它只有两项；
（3）4b²与-1的符号不统一；
（4）因为ab不是a与b的积的2倍.
2、如果x2-6x+N是一个完全平方式,那么N是( ) A . 11 B. 9 C. -11 D. -9
解析：根据完全平方式的特征，中间项-6x=2x×(-3),故可知N=(-3)2=9.
变式训练 如果x2-mx+16是一个完全平方式,那么m的值为________.
解析：∵16=(±4)2，故-m=2×(±4)，m=±8.
方法总结：本题要熟练掌握完全平方公式的结构特征， 根据参数所在位置，结合公式，找出参数与已知项之间的数量关系，从而求出参数的值.计算过程中，要注意积的2倍的符号，避免漏解．
3、把下列完全平方公式分解因式：(1)1002－2×100×99+99²；(2)342＋34×32＋162.
解：(1)原式=（100－99)²
(2)原式＝(34＋16)2
4、已知x2－4x＋y2－10y＋29＝0，求x2y2＋2xy＋1的值．
解：∵x2－4x＋y2－10y＋29＝0，
∴(x－2)2＋(y－5)2＝0.
∵(x－2)2≥0，(y－5)2≥0，
∴x－2＝0，y－5＝0，
∴x2y2＋2xy＋1＝(xy＋1)2
a2±2ab+b2=(a±b)2
（1）要求多项式有三项.（2）其中两项同号，且都可以写成某数或式的平方，另一项则是这两数或式的乘积的2倍，符号可正可负.