北师大版八年级下册2 直角三角形课文内容ppt课件

这是一份北师大版八年级下册2 直角三角形课文内容ppt课件，共21页。PPT课件主要包含了什么是勾股定理，在△ABC中，ABDC，ACDB，SSS，SAS，则∠ABC＝∠DEF等内容，欢迎下载使用。

一、创设情境，激活思维
1.判断两个三角形全等的方法有哪几种？
1.SSS、SAS、AAS、ASA。
2.直角三角形两直角边的平方和等于斜边的平方。
思考：两边分别相等且一组等边的对角相等的两个三角形全等吗？如果其中一组等边所对的角是直角呢？
二、问题探究，思维生长
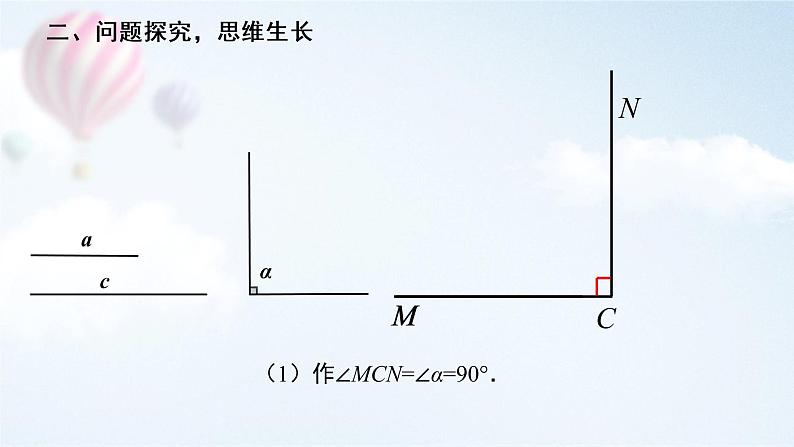
1.活动一：动手操作，猜想结论已知：线段ɑ、c（ɑ＜c），直角α．求作：Rt△ABC，使∠C＝∠α，BC＝ɑ，AB＝c．
（1）作∠MCN=∠α=90°．
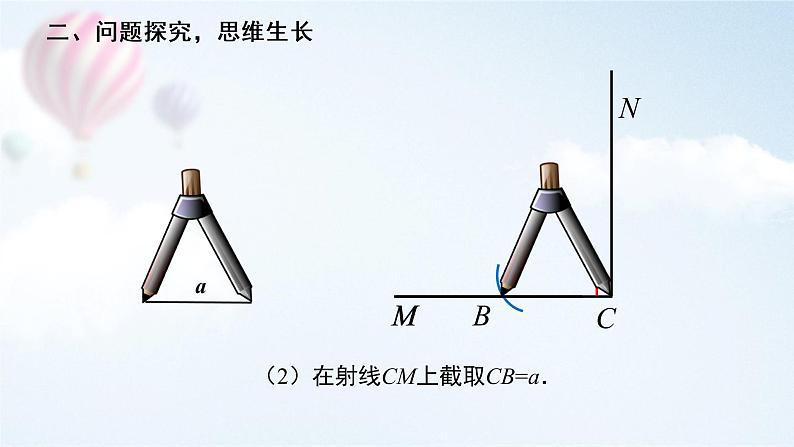
（2）在射线CM上截取CB=ɑ．
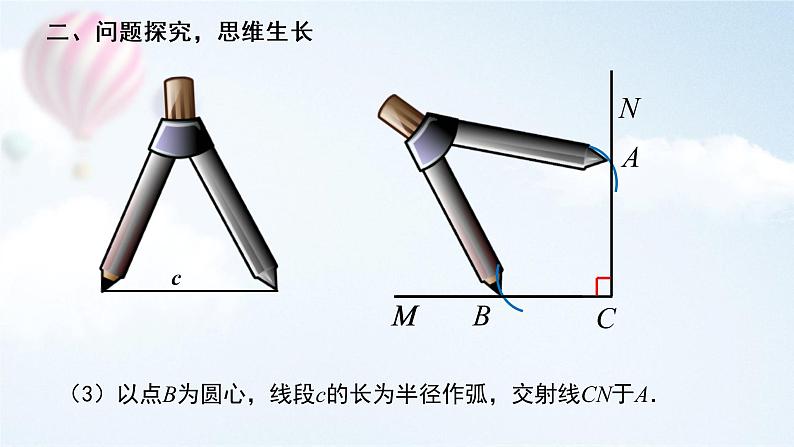
（3）以点B为圆心，线段c的长为半径作弧，交射线CN于A．
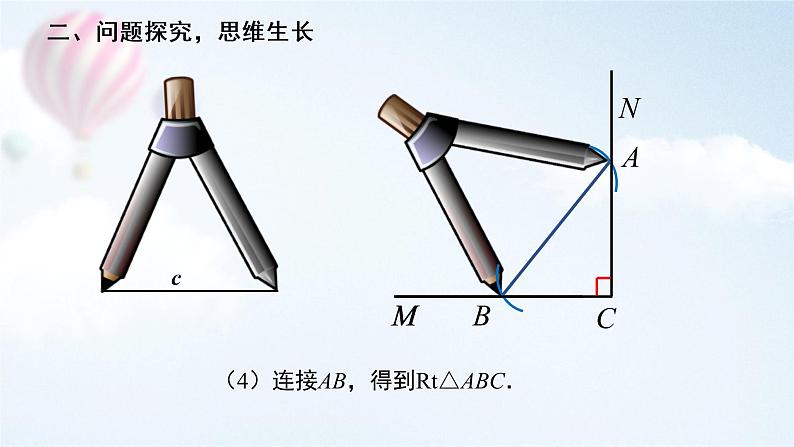
（4）连接AB，得到Rt△ABC．
1.活动一：动手操作，猜想结论你作的三角形和身边小伙伴作的三角形全等吗？
通过画图和观察，你发现了什么结论？写下来。
小组内交流，写下你认为正确的结论。
结论：斜边和一条直角边分别相等的两个直角三角形全等.
2.活动二：引导推理，论证结论
已知：在△ABC和△A′B′C′中，∠C=∠C′=90°，AB=A′B′，AC=A′C′．求证：△ABC≌△A′B′C′．
已知：在△ABC和△A′B′C′中，∠C=∠C′=90°，AB=A′B′，AC=A′C′．求证：△ABC≌△A′B′C′
∴△ABC≌△A′B′C′（SSS）．
∵∠C=90°，∴BC2=AB2-AC2（勾股定理）．
∵AB=A′B′,AC=A′C′，
同理，B′C′2=A′B′2-A′C′2．
定理：斜边和一条直角边分别相等的两个直角三角形全等(简述为“斜边、直角边”或“HL”).
几何语言：在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF (HL).
3.活动三：反思质疑，深化知识
已知AB=DE，AC=DF，∠B=∠E．
4.活动四：运用定理，解决问题
（1）如图，在Rt△ABC与Rt△DCB中，已知∠A＝∠D＝90°，若利用“HL”证明Rt△ABC≌Rt△DCB，你添加的条件是 ．（不添加字母和辅助线）
（2）下列不能使两个直角三角形全等的条件是（　　）A．三边对应相等B．两个锐角相等C．一条直角边和斜边对应相等D．两条直角边对应相等
三、典型例题，巩固新知
1．如图，幼儿园的滑梯有两个长度相等滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等．（1）△ABC与△DEF全等吗？（2）两个滑梯的倾斜角∠ABC与∠DFE的大小有什么关系．
解：△ABC与△DEF全等
理由如下：在Rt△ABC与Rt△DEF中，
∴Rt△ABC≌Rt△DEF（HL）
解：∠ABC+∠DFE＝90°
理由如下：由（1）知，Rt△ABC≌Rt△DEF，
∴∠ABC+∠DFE＝90°．
∵∠DEF+∠DFE＝90°，
四、归纳小结，反思提高
回忆本节课探究新知识的过程，谈谈你对收获？
定理：斜边和一条直角边分别相等的两个直角三角形全等。