初中数学湘教版八年级上册2.3 等腰三角形评优课课件ppt

这是一份初中数学湘教版八年级上册2.3 等腰三角形评优课课件ppt，文件包含湘教版8上数学第二章232《等腰三角形的判定》课件ppt、湘教版8上数学第二章232《等腰三角形的判定》教案docx等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。
湘教版初中数学八年级上册《等腰三角形的性质》教学设计课题名等腰三角形的性质教学目标知识与技能：理解掌握等腰三角形、等边三角形的判定，并能灵活运用判定方法解题。过程与方法：通过操作、观察、交流、逻辑推理、总结归纳等活动，探究学习等腰三角形和等边三角形的判定方法并解题。情感态度：培养学生的动手操作能力、观察能力、逻辑推理能力、总结归纳能力，获得必需的数学知识，激发学生的学习兴趣。教学重点等腰三角形、等边三角形的判定方法。教学难点根据已知条件选择正确的判定方法解题。教学准备教师准备：制作《等腰三角形的判定》课件。学生准备：剪一个等腰三角形和一个等边三角形，课前预习课本第63～65页的《等腰三角形的判定》。教学过程一、        温故知新 1、若等腰三角形的一个内角是300，求这个等腰三角形的其它内角。解：当这个等腰三角形的顶角为300， 则两底角的度数为：
  （1800-300） ÷2=750
当这个等腰三角形的一个底角为300， 则另一底角的度数也为300 ，顶角度数为：
  1800-300 × 2=1200
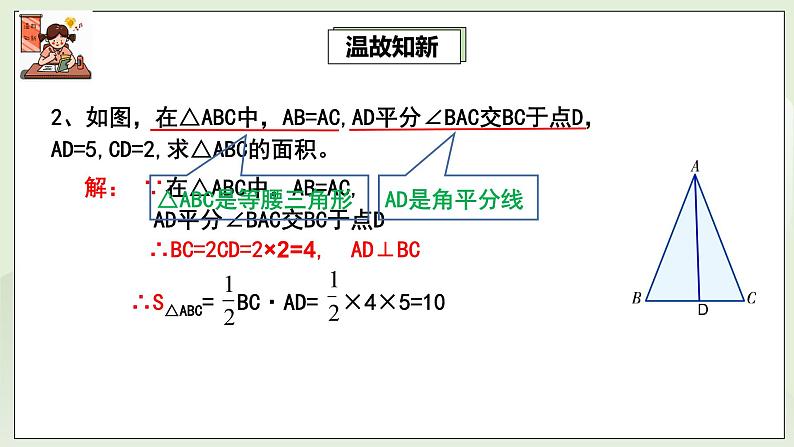
∴综上所述，这个等腰三角形的其它内角为750、750 或300、1200。2、如图，在△ABC中，AB=AC,AD平分∠BAC交BC于点D，AD=5,CD=2,求△ABC的面积。
解： ∵在△ABC中，AB=AC,
      AD平分∠BAC交BC于点D
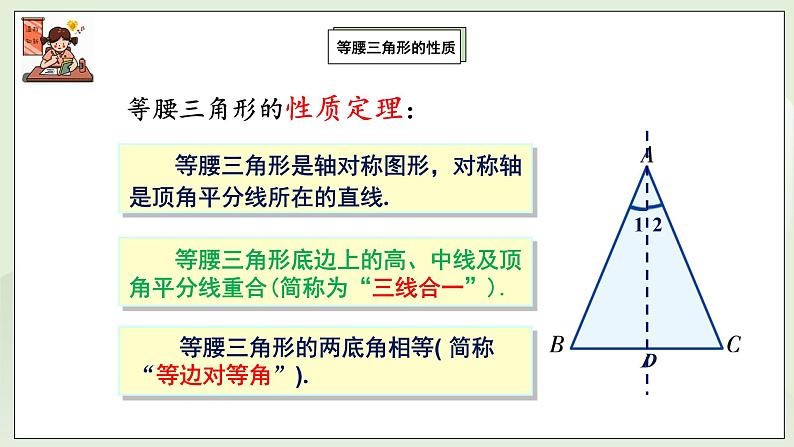
     ∴BD=CD=2,  AD⊥BC∴BC=BD+CD=4∴S△ABC= BC·AD=×5×4=10二、情景导入 1、等腰三角形有哪些性质？①等腰三角形是轴对称图形，对称轴是顶角平分线所在的直线.
②等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
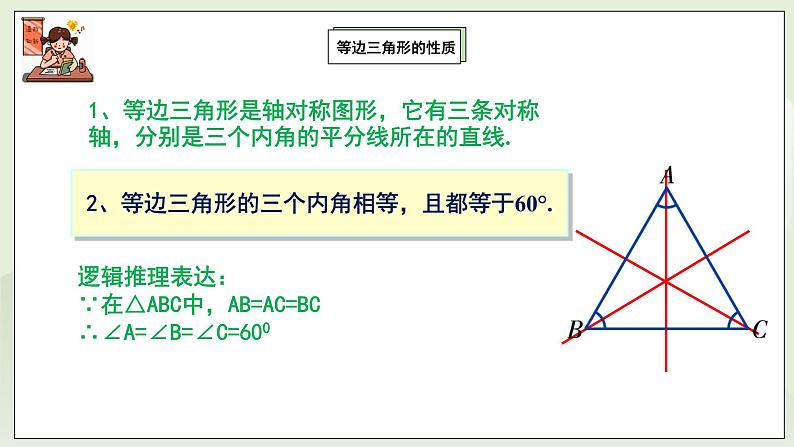
③等腰三角形的两底角相等( 简称“等边对等角”).等边三角形的性质2、等边三角形的性质①等边三角形是轴对称图形，它有三条对称轴，分别是三个内角的平分线所在的直线.
②等边三角形的三个内角相等，且都等于60°逻辑推理表达：
∵在△ABC中，AB=AC=BC
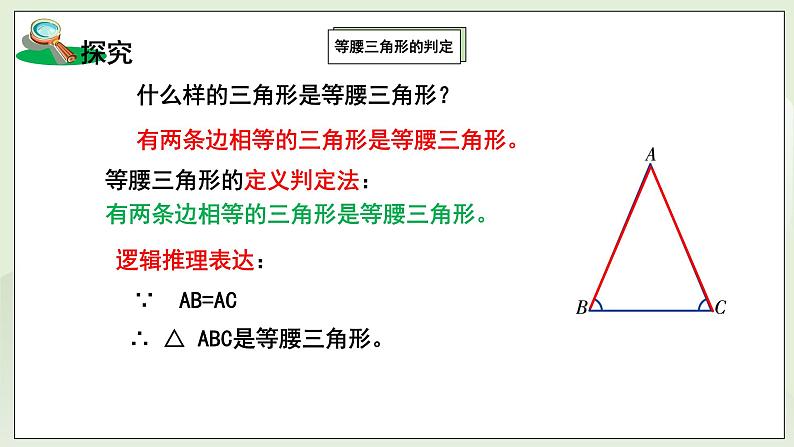
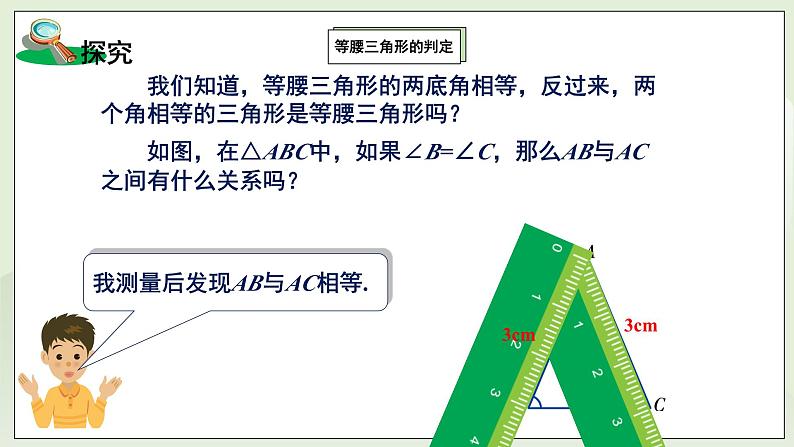
∴∠A=∠B=∠C三、新授内容（活动一）：探究等腰三角形的判断提问：等腰三角形的两底角相等，反过来，两个角相等的三角形是等腰三角形吗？如图，在△ABC中，如果∠B=∠C，那么AB与AC之间有什么关系吗？1、测量：用直尺量一量AB、AC的长度，你发现了什么？ 我测量后发现AB与AC相等。2、证明：如图，在△ABC中，∠B=∠C.
沿过点A的直线把∠BAC对折，得∠BAC的平分线AD交BC于点D，则∠1=∠2.
又∠B=∠C，所以由三角形内角和的性质得：∠ADB=∠ADC.
所以将△ABC沿AD所在直线折叠，射线DB与射线DC重合,射线DB与射线DC重合.从而点B与点C重合，于是AB=AC.
（活动二）：规律总结——等腰三角形的判定 等腰三角形的判定定理：有两个角相等的三角形是等腰三角形(简称“等角对等边”).
   逻辑推理格式表达“等角对等边”：∵ 在△ABC中， ∠B=∠C
  ∴AB=AC
（活动三）：议一议——等边三角形的判定1、提问：三角形的两角相等可以得到两边相等（等腰三角）。那么怎样可以得到三边相等（等边三角形）？答：三角形的三个角相等，就可以得到三边相等——等边三角形！2、等边三角形的判定 ：①三个角都是60°的三角形是等边三角形.
②逻辑推理格式表达：
∵ 在△ABC中，∠B=∠C=∠A=600
∴   AB=AC=BC（活动四）：做一做 ——等腰三角形的判定的应用例2  已知：如图，在△ABC中，AB=AC，点D，E分别是AB，AC上的点，且DE∥BC.
     求证：△ADE为等腰三角形.
证明 ∵AB=AC，      ∴ ∠B=∠C.
   又∵ DE∥BC，    ∴ ∠ADE=∠B，∠AED=∠C.
   ∴ ∠ADE=∠AED.         ∴ AD=AE,  即：△ADE为等腰三角形. §规律：判定一个三角形是等腰三角形，只需两底角相等或两边相等。（活动五）：动脑筋——等边三角形的判定2证明：有一个角是60°的等腰三角形是等边三角形。已知：如图，在△ABC中，AB=AC, ∠A=600
求证： △ABC是等边三角形。证明： ∵在△ABC中,∠A=600
∴ ∠B+∠C=(1800－∠A）=1200
又∵ AB=AC     ∴∠B=∠C
∴ ∠B=∠C=∠A=60°.
∴ AB=AC=BC,即△ABC是等边三角形.提问：如果底角∠B=600（或∠C=600),可以证明△ABC是等边三角形吗？§规律总结：等边三角形的判定2②    内容：有一个角是60°的等腰三角形是等边三角形。②逻辑推理格式表达：
∵ 在△ABC中，AB=AC, ∠A=600
∴AB=AC=BC
（活动六）：做一做 ——典例分析2 例3  已知：如图，△ABC是等边三角形，点D，E分别在BA，CA的延长线上，且AD=AE.
    求证：△ADE是等边三角形.证明  ∵△ABC是等边三角形，    ∴∠BAC=∠B=∠C= 60°.
∴ ∠EAD=∠BAC= 60°又∵ AD =AE，     ∴△ADE是等边三角形
（有一个角是60°的等腰三角形是等边三角形）四、课堂小测1. 已知：等腰三角形ABC的底角∠ABC和∠ACB的平分线相交于点O.
  求证：△OBC为等腰三角形.
证明：∵∠ABC和∠ACB的平分线相交于点O，∴ ∠1=∠ABC,  ∠2=∠ACB，又∵ △ABC是等腰三角形，∴ ∠ABC =∠ACB，
∴ ∠1 =∠2，    ∴ △OBC是等腰三角形.
2. 已知：如图，CD平分∠ACB，AE∥DC，AE交BC的延长线于点E，且∠ACE= 60°.
  求证：△ACE是等边三角形.证明: ∵∠ACE=60°  ∴∠ACB=1800-∠ACE=1200
∵CD平分∠ACB，  ∴ ∠1=∠2= ∠ACB=600，又∵ AE∥DC            ∴ ∠3=∠2=60°, ∠E=∠1=60°∴ ∠3=∠ACE=∠E=60°   ∴△ACE是等边三角形.3. 已知：如图，AB=BC ，∠CDE= 120°， DF∥BA，且DF平分∠CDE.
  求证：△ABC是等边三角形.
证明：∵∠CDE=120°，DF平分∠CDE.
∴ ∠1=∠FDE=∠CDA =60°
又∵DF∥BA，   ∴ ∠2=∠1=60°，∵ AB=BC，    ∴△ABC是等边三角形.布置作业课作：P66  习题2.3第5、6题家作：P67  习题2.3第7、8、9、10题并预习课本P68~P70
板书设计教学反思本节课通过学生的测量、折叠，探究学习了等腰三角形的判定和等边三角形的判定。等腰三角形、等边三角形的判定是本节的教学重点和难点，教学中需学生在学习中交流、总结归纳，让学生实践中领悟。