2020-2021学年北京市西城区三帆中学九年级10月考----无答案

2020-2021学年北京市西城区三帆中学九年级（上）月考数学试卷（10月份）

一、选择题（每题3分）

1．（3分）如图，将一张矩形的纸对折，旋转90°后再对折，然后沿着右图中的虚线剪下，则剪下的纸片打开后的形状一定为（　　）

A．三角形 B．菱形 C．矩形 D．正方形

2．（3分）如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则∠B的大小为（　　）

A．30° B．40° C．50° D．60°

3．（3分）若要得到函数y＝（x+1）2+2的图象，只需将函数y＝x2的图象（　　）

A．先向右平移1个单位长度，再向上平移2个单位长度 

B．先向左平移1个单位长度，再向上平移2个单位长度 

C．先向左平移1个单位长度，再向下平移2个单位长度 

D．先向右平移1个单位长度，再向下平移2个单位长度

4．（3分）若关于x的方程（m+1）x|m|+1﹣2x＝3是关于x的一元二次方程，则m的取值为（　　）

A．m＝1 B．m＝﹣1 C．m＝±1 D．m≠﹣1

5．（3分）⊙O是四边形ABCD的外接圆，AC平分∠BAD，则正确结论是（　　）

A．AB＝AD B．BC＝CD C．＝ D．∠BCA＝∠DCA

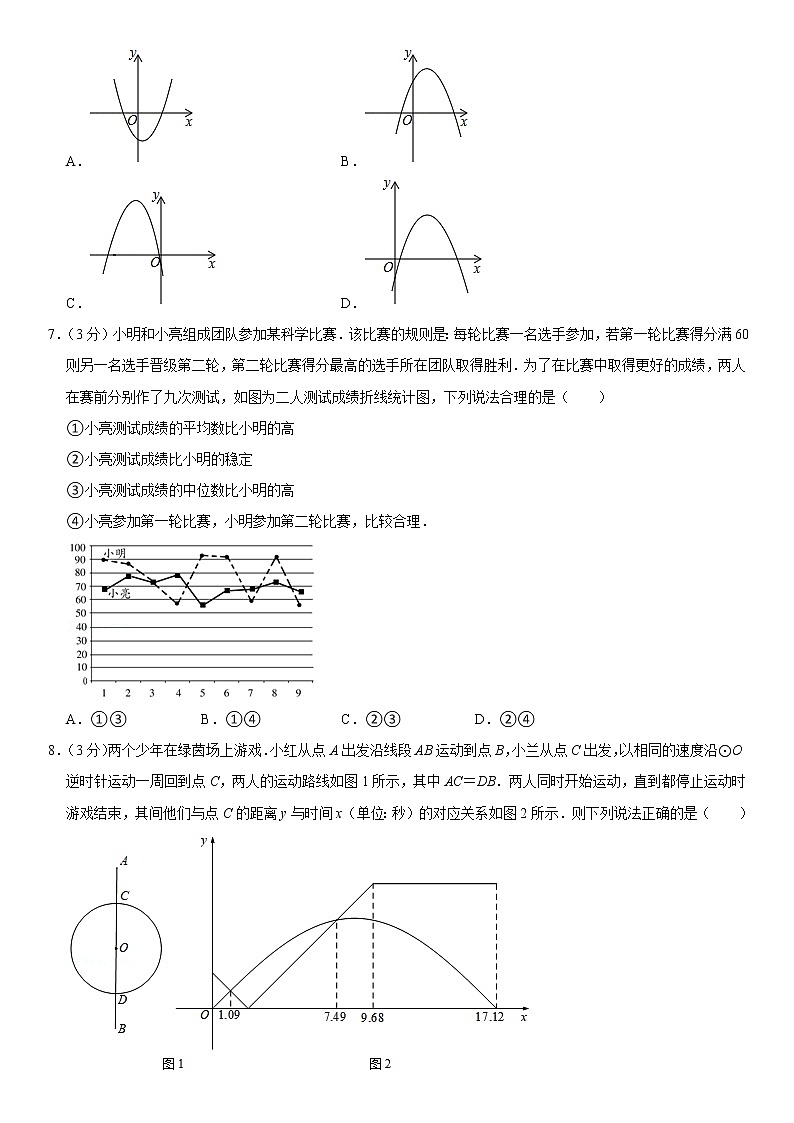
6．（3分）已知函数y＝﹣x2+bx+c，其中b＞0，c＜0，此函数的图象可以是（　　）

A． B． 

C． D．

7．（3分）小明和小亮组成团队参加某科学比赛．该比赛的规则是：每轮比赛一名选手参加，若第一轮比赛得分满60则另一名选手晋级第二轮，第二轮比赛得分最高的选手所在团队取得胜利．为了在比赛中取得更好的成绩，两人在赛前分别作了九次测试，如图为二人测试成绩折线统计图，下列说法合理的是（　　）

①小亮测试成绩的平均数比小明的高

②小亮测试成绩比小明的稳定

③小亮测试成绩的中位数比小明的高

④小亮参加第一轮比赛，小明参加第二轮比赛，比较合理．

A．①③ B．①④ C．②③ D．②④

8．（3分）两个少年在绿茵场上游戏．小红从点A出发沿线段AB运动到点B，小兰从点C出发，以相同的速度沿⊙O逆时针运动一周回到点C，两人的运动路线如图1所示，其中AC＝DB．两人同时开始运动，直到都停止运动时游戏结束，其间他们与点C的距离y与时间x（单位：秒）的对应关系如图2所示．则下列说法正确的是（　　）

A．小红的运动路程比小兰的长 

B．两人分别在1.09秒和7.49秒的时刻相遇 

C．当小红运动到点D的时候，小兰已经经过了点D 

D．在4.84秒时，两人的距离正好等于⊙O的半径

二、填空（18题4分，其余每题2分）

9．（2分）方程x2﹣2x＝0的根是　          　．

10．（2分）已知菱形ABCD中，∠B＝60°，AB＝2，则菱形ABCD的面积是　            　．

11．（2分）请写出一个开口向下，并且过坐标原点的抛物线的表达式，y＝　              　．

12．（2分）如图，在平面直角坐标系xOy中，△DEF可以看作是△ABC经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△ABC得到△DEF的过程：　                　．

13．（2分）关于x的二次函数y＝ax2﹣2ax+a﹣1（a＞0）的图象与x轴的公共点有　 　个．

14．（2分）如图，AB是⊙O的弦，C是AB的中点，连接OC并延长交⊙O于点D．若CD＝1，AB＝4，则⊙O的半径是　              　．

15．（2分）阅读以下作图过程：

第一步：在数轴上，点O表示数0，点A表示数1，点B表示数5，以AB为直径作半圆（如图）；

第二步：以B点为圆心，1为半径作弧交半圆于点C（如图）；

第三步：以A点为圆心，AC为半径作弧交数轴的正半轴于点M．

请你在下面的数轴中完成第三步的画图（保留作图痕迹，不写画法），并写出点M表示的数为　              　．

16．（2分）如图，抛物线y＝ax2+bx+c（a≠0）与y轴交于点C，与x轴交于A，B两点，其中点B的坐标为B（4，0），抛物线的对称轴交x轴于点D，CE∥AB，并与抛物线的对称轴交于点E．现有下列结论：①a＞0；②b＞0；③4a+2b+c＜0；④AD+CE＝4．其中所有正确结论的序号是　   　．

三、解答

17．解下列一元二次方程：

（1）3（1+x）2＝15；

（2）3x2﹣4x﹣2＝0．

18．已知一元二次方程x2﹣（2m﹣1）x+m2﹣m＝0．

（1）求证：此方程有两个不相等的实数根；

（2）若抛物线y＝x2﹣（2m﹣1）x+m2﹣m经过原点，求m的值．

19．已知二次函数y＝x2﹣2x﹣3．

（1）将y＝x2﹣2x﹣3化成y＝a（x﹣h）2+k的形式为　           　；

（2）此函数与x轴的交点坐标为　           　；

（3）在平面直角坐标系xOy中，画出这个二次函数的图象；（不用列表）

（4）直接写出当﹣2＜x＜3时，y的取值范围．

20．如图，菱形ABCD中，AC与BD交于点O，DE∥AC，DE＝AC．

（1）求证：四边形OCED是矩形；

（2）连接AE，交OD于点F，连接CF，若CF＝CE＝1，求AC长．

21．如图，四边形ABCD内接于⊙O，OC＝4，AC＝4．

（1）求点O到AC的距离；

（2）求∠ADC的度数．

22．小明根据学习函数的经验，对函数y＝x4﹣5x2+4的图象与性质进行了探究．

下面是小明的探究过程，请补充完整：

（1）自变量x的取值范围是全体实数，x与y的几组对应数值如下表：

其中m＝　 　；

（2）如图，在平面直角坐标系xOy中，描出了以上表中各组对应值为坐标的点，根据描出的点，画出该函数的图象；

（3）观察函数图象，写出一条该函数的性质　 　；

（4）进一步探究函数图象发现：

①方程x4﹣5x2+4＝0有　 　个互不相等的实数根；

②有两个点（x1，y1）和（x2，y2）在此函数图象上，当x2＞x1＞2时，比较y1和y2的大小关系为：y1　 　y2（填“＞”、“＜”或“＝”）；

③若关于x的方程x4﹣5x2+4＝a有4个互不相等的实数根，则a的取值范围是　 　．

23．已知二次函数y＝ax2﹣4ax+3a．

（1）该二次函数图象的对称轴是直线x＝　 　；

（2）若该二次函数的图象开口向下，当1≤x≤4时，y的最大值是2，求抛物线的解析式；

（3）若对于该抛物线上的两点P（x1，y1），Q（x2，y2），当t≤x1≤t+1，x2≥5时，均满足y1≥y2，请结合图象，直接写出t的取值范围．

24．在等腰△ABC中，AB＝AC，将线段BA绕点B顺时针旋转到BD，使BD⊥AC于H，连接AD并延长交BC的延长线于点P．

（1）依题意补全图形；

（2）若∠BAC＝2α，求∠BDA的大小（用含α的式子表示）；

（3）小明作了点D关于直线BC的对称点点E，从而用等式表示线段DP与BC之间的数量关系．请你用小明的思路补全图形并证明线段DP与BC之间的数量关系．

25．对于平面直角坐标系xOy中的点P，给出如下定义：记点P到x轴的距离为d1，到y轴的距离为d2，若d1≥d2，则称d1为点P的最大距离；若d1＜d2，则称d2为点P的最大距离．

例如：点P（﹣3，4）到x轴的距离为4，到y轴的距离为3，因为3＜4，所以点P的最大距离为4．

（1）①点A（2，﹣5）的最大距离为　 　；

②若点B（a，2）的最大距离为5，则a的值为　 　；

（2）若点C在直线y＝﹣x﹣2上，且点C的最大距离为5，求点C的坐标；

（3）若⊙O上存在点M，使点M的最大距离为5，直接写出⊙O的半径r的取值范围．