专题01 平行线的“拐点”模型-【专题突破】2021-2022学年七年级数学下学期重难点及章节分类精品讲义(人教版)

专题训练（三）平行线的“拐点”模型

1．如图，已知：AB∥CD，∠1=50°，∠2=113°，则∠3=___________度．

【答案】63

【详解】如图所示，

根据平行线的性质易知∠3＝∠2－∠1＝113°－50°＝63°.

2. 把一副三角板放在水平桌面上，摆放成如图所示的形状，使两个直角顶点重合，两条斜边平行，则∠1的度数是（　　）

A. 90° B. 105° C. 120° D. 135°

【答案】B

【详解】作直线OE平行于直角三角板的斜边．

可得：∠A＝∠AOE＝60°，∠C＝∠EOC＝45°，

故∠1的度数是：60°+45°＝105°．故选B．

3．如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是（　　）

A. α+β＝180° B. α+β＝90° C. β＝3α D. α﹣β＝90°

【答案】D

【详解】详解：过C作CF∥AB，

∵AB∥DE，

∴AB∥DE∥CF，

∴

∴故选D．

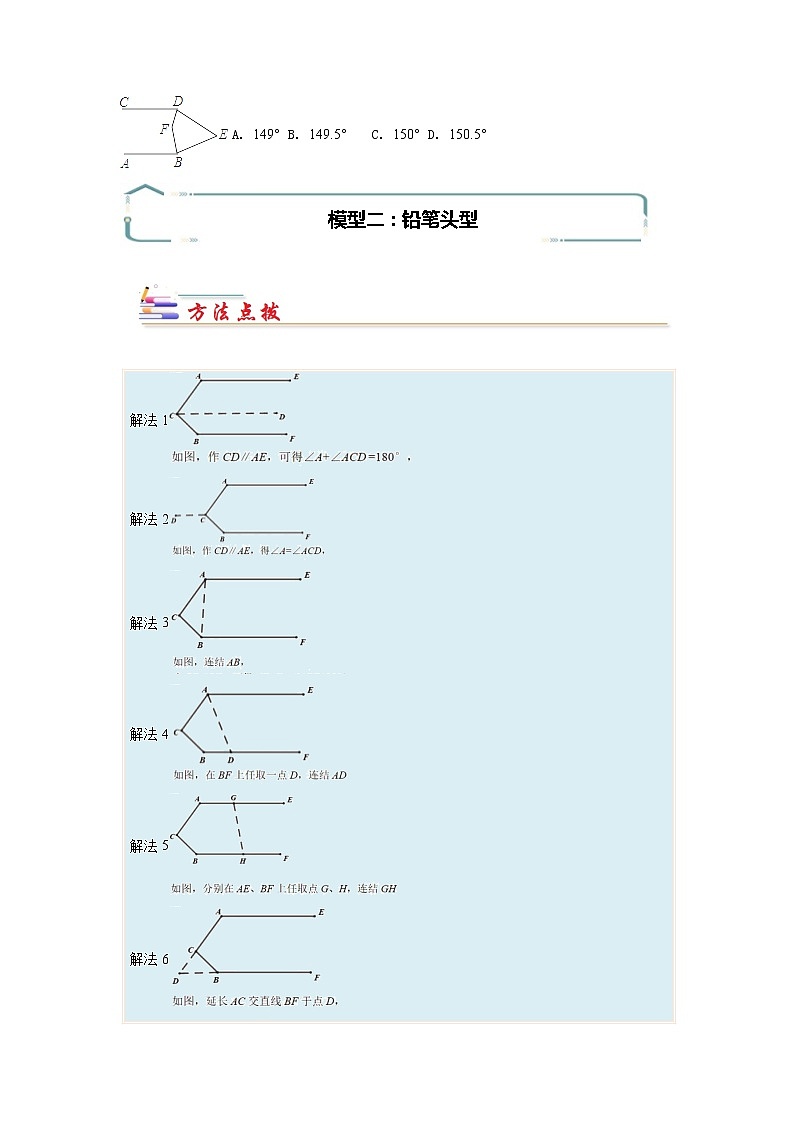
4. 如图，AB∥CD，∠BED=61°，∠ABE平分线与∠CDE平分线交于点F，则∠DFB=（　　）

A. 149° B. 149.5° C. 150° D. 150.5°

【答案】B

【详解】如图，过点E作EG∥AB，

∵AB∥CD，

∴AB∥CD∥GE，

∴∠ABE+∠BEG=180°，∠GED+∠EDC=180°，

∴∠ABE+∠CDE+∠BED=360°；

又∵∠BED=61°，

∴∠ABE+∠CDE=299°．

∵∠ABE和∠CDE的平分线相交于F，

∴∠FBE+∠EDF=（∠ABE+∠CDE）=149.5°，

∵四边形的BFDE的内角和为360°，

∴∠BFD=360°-149.5°-61°=149.5°．故选B．

5. 如图所示，l1∥l2，∠1＝105°，∠2＝140°，则∠3的度数为(　　)

A. 55° B. 60° C. 65° D. 70°

【答案】C

【详解】

过点A作AB∥l1，

∵l1∥l2，∴AB∥l1∥l2，

∴∠1+∠4=180,∠2+∠5=180，

∵∠1=105,∠2=140 ，

∴∠4=75,∠5=40，

∵∠4+∠5+∠3=180，

∴∠3=65.故答案选：C.

6. 如图，在五边形中满足，则图形中的的值是______．

【答案】85

【详解】∵AB∥CD，∠C＝60°，

∴∠B＝180°−∠C＝120°．

∴（5−2）×180°＝x°＋150°＋125°＋60°＋120°．

∴x＝85．故答案为：85．

7. 如图，已知∠ABC=80°，∠CDE=140°，则∠BCD=_____．

【答案】

【详解】延长交BC于M，

∵

∴∠BMD=∠ABC=80°，

∴；

又∵∠CDE=∠CMD+∠C，

∴．

故答案是：40°

8. 如图，AB∥CD，则∠1+∠3—∠2的度数等于__________．

【答案】180°

【详解】∵AB∥CD

∴∠1=∠EFD

∵∠2+∠EFC=∠3

∠EFD=180°-∠EFC

∴∠1+∠3—∠2=180°，故答案为：180°

9. 如图，直线MA∥NB，∠A=70°，∠B=40°，则∠P=___________度．

【答案】30

【详解】根据平行线的性质，得∠A的同位角是70°，再根据三角形的外角的性质，得∠P＝70°−40°＝30°．故答案为30．

10. 如图，AB∥CD，∠E＝37°，∠C＝20°，则∠EAB的度数为__________．

【答案】57°

【详解】设AE、CD交于点F，

∵∠E＝37°，∠C＝20°，

∴∠CFE=180°-37°-20°=123°，

∴∠AFD=123°，

∵AB∥CD，

∴∠AFD+∠EAB=180°，

∴∠EAB=180°-123°=57°，

故答案为：57°．

11. 如图，玲玲在美术课上用丝线绣成了一个“2”，AB∥DE，∠A=30°，∠ACE=110°，则∠E的度数为（　　）

A. 30° B. 150° C. 120° D. 100°

【答案】D

【详解】过C作CQ∥AB，

∵AB∥DE，

∴AB∥DE∥CQ，

∵∠A=30°，

∴∠A=∠QCA=30°，∠E+∠ECQ=180°，

∵∠ACE=110°，

∴∠ECQ=110°−30°=80°，

∴∠E=180°−80°=100°，故选D.

12. 如图所示，AB∥CD，则∠A+∠E+∠F+∠C等于（）

A. 180° B. 360° C. 540° D. 720°

【答案】C

【详解】作EM∥AB，FN∥AB，

∵AB∥CD，∴AB∥EM∥FN∥CD．
∴∠A+∠AEM=180°，∠MEF+∠EFN=180°，∠NFC+∠C=180°，
∴∠A+∠AEF+∠EFC+∠C=540°．故选：C．

13. 珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同，如图，若∠ABC=120°，∠BCD=80°，则∠CDE=__________度．

【答案】20【详解】过点C作CF∥AB，

已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同，

∴AB∥DE，CF∥DE，

∴∠BCF+∠ABC=180°，

∴∠BCF=60°，

∴∠DCF=20°，

∴∠CDE=∠DCF=20°．

故答案为20．