2020-2021学年北京市人大附中高二（上）期中数学试卷

这是一份2020-2021学年北京市人大附中高二（上）期中数学试卷，共30页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2020-2021学年北京市人大附中高二（上）期中数学试卷
一、选择题（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.）
1．（5分）若复数（1﹣i）（a+i）在复平面内对应的点在第二象限，则实数a的取值范围是（　　）
A．（﹣∞，1） B．（﹣∞，﹣1） C．（1，+∞） D．（﹣1，+∞）
2．（5分）在空间直角坐标系中，已知点A（1，0，1），B（3，2，1），则线段AB的中点的坐标是（　　）
A．（1，1，1） B．（2，1，1） C．（1，1，2） D．（1，2，3）
3．（5分）设m是一条直线，α、β是两个不同的平面，则下列命题一定正确的是（　　）
A．若α⊥β，m⊥α，则m∥β B．若α⊥β，m∥α，则m⊥β
C．若α∥β，m⊥α，则m⊥β D．若α∥β，m∥α，则m∥β
4．（5分）若直线ax+2y﹣1＝0与直线2x﹣3y﹣6＝0垂直．则a的值为（　　）
A．0 B．1 C．2 D．3
5．（5分）如图，空间四边形OABC中，，点M在上，且OM＝2MA，点N为BC中点，则＝（　　）

A． B．
C． D．
6．（5分）已知二面角α﹣AB﹣β的平面角是锐角θ，α内一点C到β的距离为3，点C到棱AB的距离为4，那么tanθ的值等于（　　）
A． B． C． D．
7．（5分）如果向量＝（2，﹣1，3）、＝（﹣1，4，﹣2）、＝（7，﹣7，m）共面，则实数m的值是（　　）
A．11 B．8 C．7 D．1
8．（5分）在边长为2的等边三角形ABC中，点D、E分别是边AC，AB上的点，满足DE∥BC且＝λ（λ∈（0，1）），将△ADE沿直线DE折到△A′DE的位置，在翻折过程中，下列结论成立的是（　　）
A．在边A′E上存在点P，使得在翻折过程中，满足BP∥平面A′CD
B．存在λ∈（0，），使得在翻折过程中的某个位置，满足平面A′BC⊥平面BCDE
C．若λ＝，当二面角A′﹣DE﹣B为直二面角时，|A′B|＝
D．设O为线段ED的中点，F为线段BC的中点，对于每个给定的λ，记翻折过程中△A′OF面积的最大值为f（λ），则当λ变化时，f（λ）的最大值为
二、填空题（本大题共6小题，每小题5分，共30分.）
9．（5分）复数+的虚部是　 　．
10．（5分）若三点A（0，8），B（﹣4，0），C（m，﹣4）共线，则实数m的值为　 　．
11．（5分）直线l：2x+2y﹣1＝0的倾斜角为　 　；经过点（1，1）且与直线l平行的直线方程为　 　．
12．（5分）请从正方体ABCD﹣A1B1C1D1的8个顶点中，找出4个点构成一个三棱锥，使得这个三棱锥的4个面都是直角三角形，则这4个点可以是　 　．（只需写出一组）

13．（5分）在棱长为1的正方体ABCD﹣A1B1C1D1中，O1是上底面A1B1C1D1的中心，M是棱BB1的中点，则四面体O1﹣ADM的体积等于　 　．
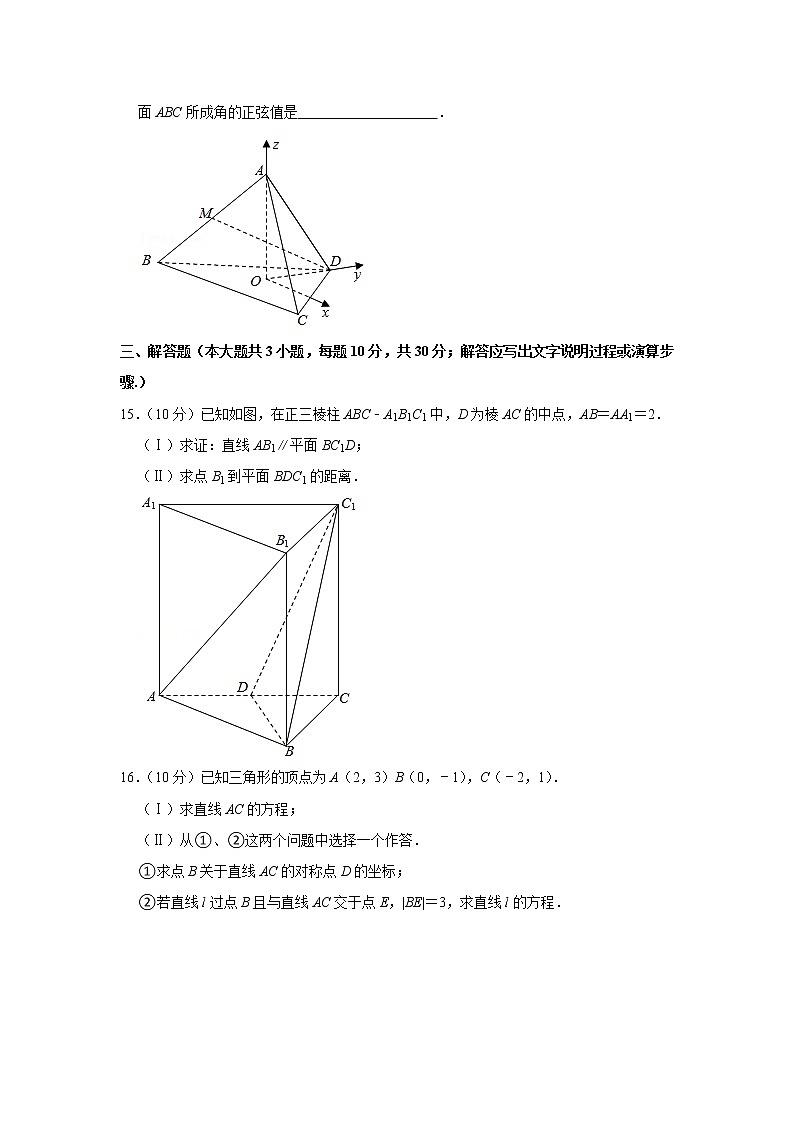
14．（5分）已知棱长为2的正四面体ABCD，如图建立直角坐标系，点O为点A在底面BCD上的射影，M为线段AB的中点、则M点坐标是　 　；直线DM与平面ABC所成角的正弦值是　 　．

三、解答题（本大题共3小题，每题10分，共30分；解答应写出文字说明过程或演算步骤.）
15．（10分）已知如图，在正三棱柱ABC﹣A1B1C1中，D为棱AC的中点，AB＝AA1＝2．
（Ⅰ）求证：直线AB1∥平面BC1D；
（Ⅱ）求点B1到平面BDC1的距离．

16．（10分）已知三角形的顶点为A（2，3）B（0，﹣1），C（﹣2，1）．
（Ⅰ）求直线AC的方程；
（Ⅱ）从①、②这两个问题中选择一个作答．
①求点B关于直线AC的对称点D的坐标；
②若直线l过点B且与直线AC交于点E，|BE|＝3，求直线l的方程．

17．（10分）已知在四棱锥P﹣ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，CD⊥平面PAD，E、F、G、O分别是PC、PD、BC、AD的中点．
（Ⅰ）求证：PO⊥平面ABCD；
（Ⅱ）求二面角B﹣EG﹣F的余弦值；
（Ⅲ）线段PB上是否存在点M，使得直线GM与平面EFG所成角为，若存在，求线段PM的长度；若不存在，说明理由．

四、选择题(本大题共3小题，每小题6分，共18分在每小题给出的四个选项中，只有一项是符合题目要求的，)
18．（6分）下面三条直线l1：3x+y＝4，l2：x﹣y＝0；l3：2x﹣3my＝4不能构成三角形，则m的范围是（　　）
A．{﹣} B．{，﹣}
C．{﹣，，﹣} D．{﹣，，0，﹣}
19．（6分）直线xsinα+y+1＝0（α∈R）的倾斜角的取值范围是（　　）
A．[﹣，] B．[，]
C．[0，]∪[，π） D．[0，]∪[，π）
20．（6分）与正方体ABCD﹣A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点（　　）
A．有且只有1个 B．有且只有2个
C．有且只有3个 D．有无数个
五、填空题(本大题共3小题，每小题6分，共18分.)
21．（6分）设复数z1，z2满足|z1|＝|z2|＝2，且z1+z2＝﹣i，其中i为虚数单位，则|z1﹣z2|＝　 　．
22．（6分）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA＝AD＝CD＝2，BC＝3，E为PD的中点，点F在线段PC上，且＝，若点Q是四棱锥P﹣ABCD表面上的一点（不含点D），DQ∥平面AEF，则线段DQ长度的取值范围是　 　．

23．（6分）已知三棱锥P﹣ABC的底面ABC为正三角形，点A在侧面PBC上的射影H是△PBC的垂心（三角形的垂心是三角形三条高线的交点），延长PH交BC于D．过P作PO⊥AD于O，延长CO交AB于F，二面角H﹣AB﹣C为，且PA＝2．则下列结论成立的有　 　．
①BC⊥AD；
②二面角P﹣AB﹣C的平面角为∠PBC；
③直线PA与平面ABC所成角的大小为；
④直线FD与直线PC所成角的余弦值为；
⑤三棱锥P﹣ABC的体积为．

六、解答题（本大题共1小题。满分14分，解答应写出文字说明过程或演算步骤.）
24．（14分）已知四棱锥T﹣ABCD的底面是平行四边形，平面α与直线AD，TA，TC分别交于点P，Q，R且＝＝＝x，点M在直线TB上，N为CD的中点，且直线MN∥平面α．
（Ⅰ）设＝，＝，＝，试用基底{，，}表示向量；
（Ⅱ）证明：四面体TABC中至少存在一个顶点，从其出发的三条棱能够组成一个三角形；
（Ⅲ）证明：对所有满足条件的平面α，点M都落在某一条长为TB的线段上．


2020-2021学年北京市人大附中高二（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.）
1．（5分）若复数（1﹣i）（a+i）在复平面内对应的点在第二象限，则实数a的取值范围是（　　）
A．（﹣∞，1） B．（﹣∞，﹣1） C．（1，+∞） D．（﹣1，+∞）
【分析】复数（1﹣i）（a+i）＝a+1+（1﹣a）i在复平面内对应的点在第二象限，可得，解得a范围．
【解答】解：复数（1﹣i）（a+i）＝a+1+（1﹣a）i在复平面内对应的点在第二象限，
∴，解得a＜﹣1．
则实数a的取值范围是（﹣∞，﹣1）．
故选：B．
【点评】本题考查了复数的运算法则、几何意义、不等式的解法，考查了推理能力与计算能力，属于基础题．
2．（5分）在空间直角坐标系中，已知点A（1，0，1），B（3，2，1），则线段AB的中点的坐标是（　　）
A．（1，1，1） B．（2，1，1） C．（1，1，2） D．（1，2，3）
【分析】利用中点坐标公式直接求解．
【解答】解：∵在空间直角坐标系中，
点A（1，0，1），B（3，2，1），
∴线段AB的中点的坐标是（2，1，1）．
故选：B．
【点评】本题考查线段中点坐标的求法，考查中点坐标公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．
3．（5分）设m是一条直线，α、β是两个不同的平面，则下列命题一定正确的是（　　）
A．若α⊥β，m⊥α，则m∥β B．若α⊥β，m∥α，则m⊥β
C．若α∥β，m⊥α，则m⊥β D．若α∥β，m∥α，则m∥β
【分析】由空间中直线与直线、直线与平面、平面与平面位置关系逐一核对四个选项得答案．
【解答】解：对于A，若α⊥β，m⊥α，则m∥β或m⊂β，故A错误；
对于B，若α⊥β，m∥α，则m∥β或m⊂β或m与β相交，故B错误；
对于C，若α∥β，m⊥α，则m⊥β，故C正确；
对于D，若α∥β，m∥α，则m∥β或m⊂β，故D错误．
故选：C．
【点评】本题考查空间中直线与直线、直线与平面、平面与平面位置关系的判定及其应用，考查空间想象能力与思维能力，是中档题．
4．（5分）若直线ax+2y﹣1＝0与直线2x﹣3y﹣6＝0垂直．则a的值为（　　）
A．0 B．1 C．2 D．3
【分析】根据直线相互垂直与斜率之间的关系即可得出．
【解答】解：∵直线ax+2y﹣1＝0与直线2x﹣3y﹣6＝0垂直，
∴﹣×（﹣）＝﹣1，
解得a＝3．
故选：D．
【点评】本题考查了直线相互垂直与斜率之间的关系，考查了推理能力与计算能力，属于基础题．
5．（5分）如图，空间四边形OABC中，，点M在上，且OM＝2MA，点N为BC中点，则＝（　　）

A． B．
C． D．
【分析】由题意，把，，三个向量看作是基向量，由图形根据向量的线性运算，将用三个基向量表示出来，即可得到答案，选出正确选项．
【解答】解：由题意
＝++
＝+﹣+
＝﹣++﹣
＝﹣++
又＝，＝，＝
∴＝﹣++
故选：B．

【点评】本题考点是空间向量基本定理，考查了用向量表示几何的量，向量的线性运算，解题的关键是根据图形把所研究的向量用三个基向量表示出来，本题是向量的基础题．
6．（5分）已知二面角α﹣AB﹣β的平面角是锐角θ，α内一点C到β的距离为3，点C到棱AB的距离为4，那么tanθ的值等于（　　）
A． B． C． D．
【分析】根据已知条件作出图形，根据图形即可找到角θ，根据已知的边的长度即可求出tanθ．
【解答】解：如图所示，CO⊥β，垂足为O，CD⊥AB，垂足为D，且CO＝3，CD＝4，连接DO，
∵CO⊥β，∴CO⊥DO，
∴在Rt△CDO中，DO＝；
∵CO⊥β，AB⊂β，
∴CO⊥AB，即AB⊥CO，又AB⊥CD，CD∩CO＝C；
∴AB⊥平面CDO，DO⊂平面CDO，∴AB⊥DO；
∴∠CDO是二面角α﹣AB﹣β的平面角，∴∠CDO＝θ；
∴．
故选：D．

【点评】考查二面角以及二面角的平面角的概念，而借助图形会比较形象的求解本题，以及线面垂直的判定定理．
7．（5分）如果向量＝（2，﹣1，3）、＝（﹣1，4，﹣2）、＝（7，﹣7，m）共面，则实数m的值是（　　）
A．11 B．8 C．7 D．1
【分析】设，列出方程组，能求出实数m的值．
【解答】解：∵向量＝（2，﹣1，3）、＝（﹣1，4，﹣2）、＝（7，﹣7，m）共面，
∴设，即（2，﹣1，3）＝（﹣x，4x，﹣2x）+（7y，﹣7y，my）＝（7y﹣x，4x﹣7y，my﹣2x），
∴，解得．
∴实数m的值是11．
故选：A．
【点评】本题考查实数值的求法，考查共面向量的性质等基础知识，考查运算求解能力，是基础题．
8．（5分）在边长为2的等边三角形ABC中，点D、E分别是边AC，AB上的点，满足DE∥BC且＝λ（λ∈（0，1）），将△ADE沿直线DE折到△A′DE的位置，在翻折过程中，下列结论成立的是（　　）
A．在边A′E上存在点P，使得在翻折过程中，满足BP∥平面A′CD
B．存在λ∈（0，），使得在翻折过程中的某个位置，满足平面A′BC⊥平面BCDE
C．若λ＝，当二面角A′﹣DE﹣B为直二面角时，|A′B|＝
D．设O为线段ED的中点，F为线段BC的中点，对于每个给定的λ，记翻折过程中△A′OF面积的最大值为f（λ），则当λ变化时，f（λ）的最大值为
【分析】根据线面平行的性质判断A，根据直角三角形的性质判断B，根据勾股定理计算|A′B|判断C，利用基本不等式判断D．
【解答】解：对于A，连接AA′，A′B，A′C，显然平面A′BE∩平面A′CD＝AA′，
若A′E上存在点F使得BF∥A′CD，则BF∥AA′，显然BF与AA′为相交直线，矛盾，故A错误；
对于B，设BC中点F，DE中点O，由等边三角形性质可知DE⊥AO，DE⊥A′O，
故A′在平面BCDE上的射影在直线AF上，
若平面A'BC⊥平面BCDE，则F为A′在底面BCDE上的射影，于是A′O＞OF，
∴λ＞，与λ∈（0，）矛盾，故B错误；
对于C，若，二面角A'﹣DE﹣B为直二面角，则OA′＝OF＝AF＝，BF＝1，
且A′O⊥平面BCDE，∵OB＝＝，
∴|AB′|＝＝，故C错误；
对于D，由可知AO＝λ，即A′O＝λ，∴OF＝﹣λ，
显然当A′O⊥OF时，△A′OF的面积最大，故f（λ）＝×（）＝λ（1﹣λ）≤×（）2＝，
当且仅当λ＝1﹣λ即λ＝时取等号，故D正确．
故选：D．

【点评】本题考查了线面平行的性质，空间距离与空间角的计算，考查基本不等式的应用，属于中档题．
二、填空题（本大题共6小题，每小题5分，共30分.）
9．（5分）复数+的虚部是　　．
【分析】利用复数的运算法则和虚部的定义即可得出．
【解答】解：复数+＝＝＝．
故其虚部为．
故答案为．
【点评】熟练掌握复数的运算法则和虚部的定义是解题的关键．
10．（5分）若三点A（0，8），B（﹣4，0），C（m，﹣4）共线，则实数m的值为　﹣6　．
【分析】由三点A（0，8），B（﹣4，0），C（m，﹣4）共线，可得kAB＝kBC，解出即可得出．
【解答】解：三点A（0，8），B（﹣4，0），C（m，﹣4）共线，则kAB＝kBC，
可得：＝，
解得：m＝﹣6．
经过验证可知满足题意．
实数m的值为﹣6．
【点评】本题考查了三点共线与直线斜率之间的关系，考查了推理能力与计算能力，属于基础题．
11．（5分）直线l：2x+2y﹣1＝0的倾斜角为　135°　；经过点（1，1）且与直线l平行的直线方程为　x+y﹣2＝0　．
【分析】先求出直线的斜率，可得它的倾斜角，再用点斜式求出要求直线的方程．
【解答】解：∵直线l：2x+2y﹣1＝0的斜率为﹣1，∴它的倾斜角为135°；
经过点（1，1）且与直线l平行的直线方程为y﹣1＝﹣1×（x﹣1），即 x+y﹣2＝0，
故答案为：135°； x+y﹣2＝0．
【点评】本题考查了直线的斜率和倾斜角，用点斜式求直线的方程，考查了推理能力与计算能力，属于基础题．
12．（5分）请从正方体ABCD﹣A1B1C1D1的8个顶点中，找出4个点构成一个三棱锥，使得这个三棱锥的4个面都是直角三角形，则这4个点可以是　A1、A、C、D　．（只需写出一组）

【分析】正方体ABCD﹣A1B1C1D1中，由CD⊥平面ADD1A1，AA1⊥平面ABCD，得到从正方体ABCD﹣A1B1C1D1的8个顶点中，找出4个点A1、A、C、D，构成一个三棱锥A1﹣ACD，这个三棱锥的4个面都是直角三角形．
【解答】解：∵正方体ABCD﹣A1B1C1D1中，CD⊥平面ADD1A1，
∴A1D⊥CD，AD⊥CD，AA1⊥CD，
∵正方体ABCD﹣A1B1C1D1中，AA1⊥平面ABCD，
∴AA1⊥AD，AA1⊥AC，
∴从正方体ABCD﹣A1B1C1D1的8个顶点中，找出4个点A1、A、C、D，
构成一个三棱锥A1﹣ACD，这个三棱锥的4个面都是直角三角形．
故答案为：A1、A、C、D．

【点评】本题正方体的八个顶点中能构成4个面都是直角三角形的三棱锥的顶点的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、函数与方程思想，是中档题．
13．（5分）在棱长为1的正方体ABCD﹣A1B1C1D1中，O1是上底面A1B1C1D1的中心，M是棱BB1的中点，则四面体O1﹣ADM的体积等于　　．
【分析】由题意画出图形，求出△O1DM的面积，利用等体积法求四面体O1﹣ADM的体积．
【解答】解：如图，
取面O1DM为底面，则＝＝．
四面体O1﹣ADM即三棱锥A﹣O1DM，高h为A到平面BB1D1D的距离为．
∴四面体O1﹣ADM的体积＝＝．
故答案为：．

【点评】本题考查多面体体积的求法，考查空间想象能力与思维能力，是中档题．
14．（5分）已知棱长为2的正四面体ABCD，如图建立直角坐标系，点O为点A在底面BCD上的射影，M为线段AB的中点、则M点坐标是　（﹣，﹣，）　；直线DM与平面ABC所成角的正弦值是　　．

【分析】求出A，B的坐标得出中点M的坐标，求出平面ABC的法向量，计算与的夹角得出线DM与平面ABC所成角的大小．
【解答】解：延长DO交BC于E，则DE⊥BC，E为BC的中点，
∵正四面体ABCD的棱长为2，
∴BE＝1，DE＝，OE＝DE＝，OD＝DE＝，
∴OA＝＝，
∴B（﹣1，﹣，0），A（0，0，），
∵M是AB的中点，∴M（﹣，﹣，），
又D（0，，0），∴＝（﹣，﹣，），
＝（2，0，0），＝（1，，），
设平面ABC的法向量为，则，即，
设z＝1可得＝（0，﹣2，1），
∴cos＜，＞＝＝＝，
∴直线DM与平面ABC所成角的正弦值是．
故答案为：（﹣，﹣，），．

【点评】本题考查了空间向量与线面角计算，属于中档题．
三、解答题（本大题共3小题，每题10分，共30分；解答应写出文字说明过程或演算步骤.）
15．（10分）已知如图，在正三棱柱ABC﹣A1B1C1中，D为棱AC的中点，AB＝AA1＝2．
（Ⅰ）求证：直线AB1∥平面BC1D；
（Ⅱ）求点B1到平面BDC1的距离．

【分析】（Ⅰ）取A1C1的中点D1，证明平面AB1D1∥平面C1BD，从而得出AB1∥平面BC1D；
（Ⅱ）建立空间坐标系，求出平面BDC1的法向量，根据点到平面的距离公式计算点B1到平面BDC1的距离．
【解答】（Ⅰ）证明：取A1C1的中点D1，连接AD1，DD1，
∵四边形ACC1A1是矩形，D，D1分别是AC，A1C1的中点，
∴AD∥C1D1，AD＝C1D1，
∴四边形ADC1D1是平行四边形，∴AD1∥C1D，
同理可证BD∥B1D1，
又BD∩C1D＝D，AD1∩B1D1＝D1，
∴平面AB1D1∥平面C1BD，又AB1⊂平面AB1D1，
∴AB1∥平面BC1D．
（Ⅱ）解：以D为原点，以DB，DC，DD1为坐标轴建立空间直角坐标系D﹣xyz，
则D（0，0，0），B（，0，0），C1（0，1，2），B1（，0，2），
∴＝（0，0，2），＝（，0，0），＝（0，1，2），
设平面BDC1的法向量为，则，即，
令z＝1可得＝（0，﹣2，1），
∴B1到平面BDC1的距离为＝＝．

【点评】本题考查线面平行的判定，考查点到平面的距离计算，属于中档题．
16．（10分）已知三角形的顶点为A（2，3）B（0，﹣1），C（﹣2，1）．
（Ⅰ）求直线AC的方程；
（Ⅱ）从①、②这两个问题中选择一个作答．
①求点B关于直线AC的对称点D的坐标；
②若直线l过点B且与直线AC交于点E，|BE|＝3，求直线l的方程．

【分析】（Ⅰ）直接利用点斜式，得到直线的方程；
（Ⅱ）利用中点坐标公式和直线垂直的充要条件，得到点的坐标．
【解答】解：（Ⅰ）三角形的顶点为A（2，3）B（0，﹣1），C（﹣2，1）．
所以，
所以直线AC的方程为，整理得x﹣2y+4＝0．
（Ⅱ）选①时，设点D（m，n）
所以，，故，
直线BD的中点坐标（）满足直线AC的方程，
故，解得．
故D（）．
选②时，设经过点B的直线的方程为y＝kx﹣1，与直线AC：x﹣2y+4＝0交点坐标为（x，y），
所以，解得，
由于|BE|＝3，
故，
解得k＝﹣．
故直线l的方程为．
【点评】本题考查的知识要点：直线方程，中点坐标公式，直线垂直的充要条件，主要考查学生的运算能力和转换能力及思维能力，属于基础题．
17．（10分）已知在四棱锥P﹣ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，CD⊥平面PAD，E、F、G、O分别是PC、PD、BC、AD的中点．
（Ⅰ）求证：PO⊥平面ABCD；
（Ⅱ）求二面角B﹣EG﹣F的余弦值；
（Ⅲ）线段PB上是否存在点M，使得直线GM与平面EFG所成角为，若存在，求线段PM的长度；若不存在，说明理由．

【分析】（Ⅰ）证明PO⊥AD，PO⊥CD即可得出PO⊥平面ABCD；
（Ⅱ）建立空间坐标系，计算平面BEG的法向量和平面FEG的法向量，根据法向量夹角得出二面角大小；
（Ⅲ）假设存在符合条件的点M，设＝λ，令|cos＜，＞|＝计算λ，根据λ的值作出判断即可．
【解答】（Ⅰ）证明：∵△PAD是正三角形，O是AD的中点，
∴PO⊥AD，
∵CD⊥平面PAD，PO⊂平面PAD，
∴PO⊥CD，
又AD∩CD＝D，AD⊂平面ABCD，CD⊂平面ABCD，
∴PO⊥平面ABCD．
（Ⅱ）解：连接OG，
∵四边形ABCD是正方形，∴OG⊥AD，
以O为原点，以OA，OG，OP所在直线为坐标轴建立空间直角坐标系O﹣xyz，如图所示，
则B（2，4，0），G（0，4，0），C（﹣2，4，0），P（0，0，2），D（﹣2，0，0），
∴E（﹣1，2，），F（﹣1，0，），
∴＝（0，2，0），＝（1，2，﹣），＝（2，0，0），
设平面BEG的法向量为＝（x1，y1，z1），则，即，
令z1＝2可得＝（0，，2），
设平面EFG的法向量为＝（x2，y2，z2），则，即，
令z2＝1可得＝（，0，1），
∴cos＜＞＝＝＝，
由图形可知二面角B﹣EG﹣F为锐二面角，
故二面角B﹣EG﹣F的余弦值为．
（Ⅲ）解：假设线段PB上存在点M使得GM与平面EFG所成角为，
＝（2，4，﹣2），＝（0，4，﹣2），
不妨设＝λ＝（2λ，4λ，﹣2λ），则＝﹣＝（2λ，4λ﹣4，2﹣2λ），
∴cos＜，＞＝＝＝＝，
∴||＝＝2，解得λ＝1或λ＝，
又PB＝||＝＝4，∴PM＝3或PM＝4，
故线段PB上存在点M，使得直线GM与平面EFG所成角为，PM＝3或PM＝4．

【点评】本题考查线面垂直的判定，考查空间向量与二面角、线面角的计算，属于中档题．
四、选择题(本大题共3小题，每小题6分，共18分在每小题给出的四个选项中，只有一项是符合题目要求的，)
18．（6分）下面三条直线l1：3x+y＝4，l2：x﹣y＝0；l3：2x﹣3my＝4不能构成三角形，则m的范围是（　　）
A．{﹣} B．{，﹣}
C．{﹣，，﹣} D．{﹣，，0，﹣}
【分析】由题意可得，其中有两条直线互相平行或三线共点，由此求得m的范围．
【解答】解：若三条直线l1：3x+y＝4，l2：x﹣y＝0；l3：2x﹣3my＝4不能构成三角形，
则有其中两条直线互相平行或三线共点．
由于直线l1的斜率为﹣3，直线l2的斜率为1，直线l3的斜率为，
当＝﹣3，求得m＝﹣，
当 ＝1，m＝．
若直线l1和直线l2的交点（1，1）在直线l3：2x﹣3my＝4上，求得m＝﹣，
故选：C．
【点评】本题主要考查两条直线平行的性质，3条直线共点问题，属于基础题．
19．（6分）直线xsinα+y+1＝0（α∈R）的倾斜角的取值范围是（　　）
A．[﹣，] B．[，]
C．[0，]∪[，π） D．[0，]∪[，π）
【分析】先求出直线的斜率，进而得到倾斜角正切值的范围，再利用正切函数的图象即可求出倾斜角的范围．
【解答】解：直线xsinα+y+1＝0的斜率k＝﹣，
∵﹣1≤sinα≤1，∴，
设直线的倾斜角为θ，则tan，且θ∈[0，π），
∴．
故选：D．
【点评】本题主要考查了直线的斜率和倾斜角，考查了正切函数的图象和性质，是基础题．
20．（6分）与正方体ABCD﹣A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点（　　）
A．有且只有1个 B．有且只有2个
C．有且只有3个 D．有无数个
【分析】由于点D、B1显然满足要求，猜想B1D上任一点都满足要求，然后想办法证明结论．
【解答】解：在正方体ABCD﹣A1B1C1D1上建立如图所示空间直角坐标系，
并设该正方体的棱长为1，连接B1D，并在B1D上任取一点P，
因为＝（1，1，1），
所以设P（a，a，a），其中0≤a≤1．
作PE⊥平面A1D，垂足为E，再作EF⊥A1D1，垂足为F，
则PF是点P到直线A1D1的距离．
所以PF＝；
同理点P到直线AB、CC1的距离也是．
所以B1D上任一点与正方体ABCD﹣A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离都相等，
所以与正方体ABCD﹣A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点有无数个．
故选：D．

【点评】本题主要考查合情推理的能力及空间中点到线的距离的求法．
五、填空题(本大题共3小题，每小题6分，共18分.)
21．（6分）设复数z1，z2满足|z1|＝|z2|＝2，且z1+z2＝﹣i，其中i为虚数单位，则|z1﹣z2|＝　2　．
【分析】设z1＝a+bi，z2＝c+di，（a，b，c，d∈R），根据题意可得a2+b2＝4，c2+d2＝4，ac+bd＝﹣2，代入|z1﹣z2|＝＝即可求出结果．
【解答】解：设z1＝a+bi，z2＝c+di，（a，b，c，d∈R），
∵|z1|＝|z2|＝2，∴a2+b2＝4，c2+d2＝4，
∵z1+z2＝（a+c）+（b+d）i＝，
∴a+c＝，b+d＝﹣，
∴a2+c2+2ac+b2+d2+2bd＝4，
∴ac+bd＝﹣2，
∴|z1﹣z2|＝|（a﹣c）+（b﹣d）i|＝＝＝＝2．
故答案为：2．
【点评】本题主要考查了复数的运算和复数的模长，是基础题．
22．（6分）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA＝AD＝CD＝2，BC＝3，E为PD的中点，点F在线段PC上，且＝，若点Q是四棱锥P﹣ABCD表面上的一点（不含点D），DQ∥平面AEF，则线段DQ长度的取值范围是　（0，2]　．

【分析】建立空间坐标系，利用向量确定平面AEF与PB的交点位置，过D点构造与平面AEF平行的平面，得出Q的轨迹，从而可得出DQ的范围．
【解答】解：过A作AM⊥BC于M，以AM，AD，AP为坐标轴建立空间直角坐标系，如图所示，
则B（2，﹣1，0），P（0，0，2），E（0，1，1），C（2，2，0），
∴＝（2，﹣1，﹣2），＝（0，0，2），＝（0，1，1），＝（2，2，﹣2），
∴＝+＝（，，），
设平面AEF与PB的交点为N，则存在唯一实数对λ，μ，使得＝λ+μ，
不妨设＝k＝（2k，﹣k，﹣2k），则＝＝（2k，﹣k，2﹣2k），
∴，解得，即N为线段PB的靠近B的三等分点，
连接AN，FN，取PC的中点H，CF的中点G，连接DG，MG，DM，BH，则DG∥EF，
∵，＝2，∴BH∥NF，
又，∴MG∥BH，
∴MG∥NF，
又DG∩MG＝G，EF∩NF＝F，
∴平面DMG∥平面AEF，
∵Q为四棱锥P﹣ABCD表面上的一点（不含D），DQ∥平面AEF，
∴Q的轨迹为△DMG（不含D点），
∵M（2，0，0），D（0，2，0），G（，，），
∴DM＝＝2，DG＝＝＜2，
∴0＜DQ≤2．
故答案为：（0，2]．

【点评】本题考查平面的性质，考查面面平行的性质，属于中档题．
23．（6分）已知三棱锥P﹣ABC的底面ABC为正三角形，点A在侧面PBC上的射影H是△PBC的垂心（三角形的垂心是三角形三条高线的交点），延长PH交BC于D．过P作PO⊥AD于O，延长CO交AB于F，二面角H﹣AB﹣C为，且PA＝2．则下列结论成立的有　①③⑤　．
①BC⊥AD；
②二面角P﹣AB﹣C的平面角为∠PBC；
③直线PA与平面ABC所成角的大小为；
④直线FD与直线PC所成角的余弦值为；
⑤三棱锥P﹣ABC的体积为．

【分析】延长BH交PC与M，证明BC⊥平面PAD，PC⊥平面ABM，PO⊥平面ABC，AB⊥平面PCF，可判断①，②，并得出PA＝PB＝PC，设AB＝a，根据∠MFC＝和勾股定理列方程计算a，再判断③④⑤．
【解答】解：延长BH交PC与M，连接AM，PF，FM
∵AH⊥平面PBC，∴AH⊥BC，
∵H是△PBC的垂心，∴PH⊥BC，即PD⊥BC，
又PD∩AH＝H，PD⊂平面PAD，AH⊂平面PAD，
∴BC⊥平面PAD，∴BC⊥AD，BC⊥PO，故①正确；
∵PO⊥AD，AD∩BC＝D，
∴PO⊥平面ABC，∴PO⊥AB，
∵AH⊥平面PBC，∴AH⊥PC，
∵H是△PBC的垂心，∴BM⊥PC，
又AH∩BM＝H，∴PC⊥平面ABM，
∴PC⊥AB，
又PO⊥AB，PO∩PC＝P，
∴AB⊥平面PCF，
∴AB⊥CF，AB⊥PF，AB⊥MF，
∴∠PFC是二面角P﹣AB﹣C的平面角，故②错误；
∴∠MFC是二面角H﹣AB﹣C的平面角，即∠MFC＝，
由PC⊥平面ABM可得PC⊥FM，
∴CM＝CF，FM＝CM，
∵△ABC是等边三角形，BC⊥AD，AB⊥CF，
∴D是BC的中点，F是AB的中点，O是△ABC的中心，
∴PA＝PB＝PC＝2，
设△ABC的边长为a，则CF＝AD＝a，∴CM＝a，PM＝2﹣a，FM＝，
又PF＝＝，PC⊥FM，
∴PF2＝PM2+FM2，即4﹣＝（2﹣）2+，解得：a＝，
∴AO＝AD＝a＝1，
∵PO⊥平面ABC，∴∠PAO为直线PA与平面ABC所成的角，
∴cos∠PAO＝＝，故∠PAO＝，故③正确；
∵D是BC的中点，F是AB的中点，∴DF∥AC，
∴∠PCA是直线FD与直线PC所成的角，
在△PAC中，由余弦定理可得cos∠PAC＝＝，故④错误；
∵PO＝＝，
VP﹣ABC＝S△ABC•PO＝×（）2×＝，故⑤正确．
故答案为：①③⑤．

【点评】本题考查线面垂直的判定和性质，考查空间角计算•、棱锥的体积计算，属于中档题．
六、解答题（本大题共1小题。满分14分，解答应写出文字说明过程或演算步骤.）
24．（14分）已知四棱锥T﹣ABCD的底面是平行四边形，平面α与直线AD，TA，TC分别交于点P，Q，R且＝＝＝x，点M在直线TB上，N为CD的中点，且直线MN∥平面α．
（Ⅰ）设＝，＝，＝，试用基底{，，}表示向量；
（Ⅱ）证明：四面体TABC中至少存在一个顶点，从其出发的三条棱能够组成一个三角形；
（Ⅲ）证明：对所有满足条件的平面α，点M都落在某一条长为TB的线段上．

【分析】（Ⅰ）直接根据向量的加减的几何意义即可求出；
（Ⅱ）不妨设AB是四面体最长的棱，根据三角形中的三边关系即可证明；
（Ⅲ）根据向量的加减的几何意义和向量的共线定理，以及向量的平行即可证明．
【解答】解：（Ⅰ）∵+＝+，
∴＝﹣+；
证明：（Ⅱ）不妨设AB是四面体最长的棱，
则在△ABT，△ABC中，AT+TB＞AB，AC+CB＞AB，
∴AT+TB+AC+CB＞2AB，
∴（AT+AC）+（TB+BC）＞2AB，
∴AT+AC，TB+BC至少有一个大于AB，
不妨设AT+AC＞AB，
∴AT，AC，AB能构成三角形；
证明（Ⅲ）设＝，＝，＝，
由（Ⅰ）可知＝﹣+，
∵＝＝＝x，
∴＝x，＝（1﹣x），
∵＝x，
∴＝（1﹣x）+x（+﹣）＝+x﹣x，
＝+x﹣x﹣x＝（1﹣x）+x﹣x，
＝（1﹣x）﹣x＝﹣x+（1﹣x），
设＝λ＝λ，
∵＝+＝﹣+，
＝﹣﹣＝﹣+（λ）﹣，
∵∥平面PQR，
∴存在实数y，z使得＝y+z，
∴﹣＝y（1﹣x）﹣yx+yx﹣zx+z（1﹣x），
＝（y﹣xy﹣zx）﹣yx+（yx+z﹣xz），
∴，
消元可得（4λ+1）x2﹣（4λ+3）x+2λ+1＝0，
当λ＝﹣，﹣2x+＝0，解得x＝，
当λ≠﹣，∵x∈R，
∴△＝（4λ+3）2﹣4（4λ+1）（2λ+1）≥0，
解得﹣≤λ≤，
综上﹣≤λ≤，
故对所有满足条件的平面α，点M都落在某一条长为TB的线段上．
【点评】本题考查了向量的加减的几何意义向量，共线定理，向量的平行，考查了推理论证能力，属于中档题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/10/4 9:28:54；用户：张强；邮箱：goodboyiis@163.com；学号：426909

菁优网APP 菁优网公众号 菁优网小程序