初中数学人教版九年级上册24.3 正多边形和圆一课一练

这是一份初中数学人教版九年级上册24.3 正多边形和圆一课一练，共8页。
1.________________相等，______________也相等的多边形叫做正多边形.
2．把一个圆分成几等份，连接各点所得到的多边形是________________，它的中心角等于______________________________________________.
3.一个正多边形的外接圆的____________叫做这个正多边形的中心，外接圆的__________叫做正多边形的半径，正多边形每一边所对的__________叫做正多边形的中心角，中心到正多边形的一边的____________叫做正多边形的边心距.
4.正n边形的半径为R，边心距为r，边长为a，
（1）中心角的度数为：______________.
（2）每个内角的度数为：_______________________.
（3）每个外角的度数为：____________.
（4）周长为：_________，面积为：_________.
5.正n边形都是轴对称图形，当边数为偶数时，它的对称轴有_______条，并且还是中心对称图形；当边数为奇数时，它只是_______________.（填“轴对称图形”或“中心对称图形”）
一、选择题
1.下列说法正确的是 （ ）
A.各边相等的多边形是正多边形
B.各角相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的圆内接多边形是正多边形
2.（2013•天津）正六边形的边心距与边长之比为 （ ）
3.(2013山东滨州)若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为 ( )
第4题
A．6， B．，3
C．6，3 D．，
4. 如图所示，正六边形ABCDEF内接于⊙O，
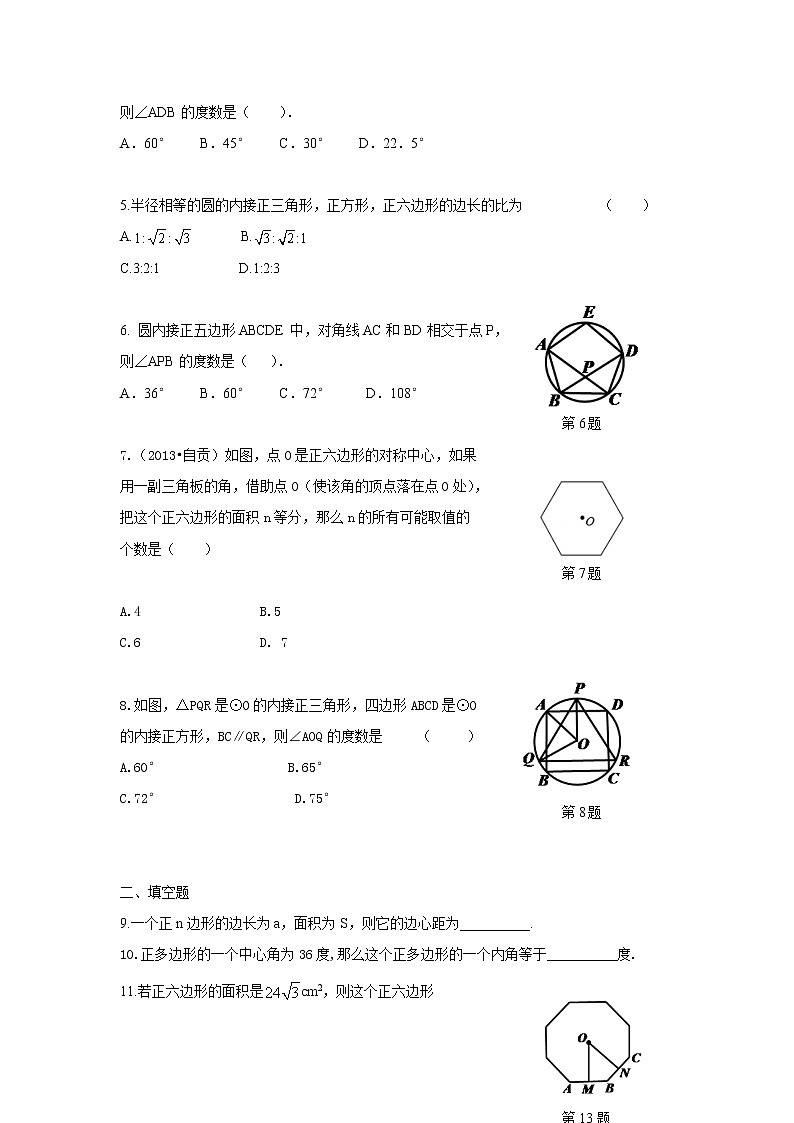
则∠ADB的度数是（ ）．
A．60° B．45° C．30° D．22．5°
5.半径相等的圆的内接正三角形，正方形，正六边形的边长的比为 （ ）
A. B.
C.3:2:1 D.1:2:3
第6题
6. 圆内接正五边形ABCDE中，对角线AC和BD相交于点P，
则∠APB的度数是（ ）．
A．36° B．60° C．72° D．108°

7.（2013•自贡）如图，点O是正六边形的对称中心，如果
第7题
用一副三角板的角，借助点O（使该角的顶点落在点O处），
把这个正六边形的面积n等分，那么n的所有可能取值的
个数是（ ）
A.4 B.5
C.6 D. 7
第8题
8.如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O
的内接正方形，BC∥QR，则∠AOQ的度数是 （ ）
A.60° B.65°
C.72° D.75°

二、填空题
9.一个正n边形的边长为a，面积为S，则它的边心距为__________.
10.正多边形的一个中心角为36度,那么这个正多边形的一个内角等于__________度.
第13题
11.若正六边形的面积是cm2，则这个正六边形
的边长是__________.
12.已知正六边形的边心距为，则它的周长是_______.
13.点M、N分别是正八边形相邻的边AB、BC上的点，且AM
=BN，点O是正八边形的中心，则∠MON=_____________.
14.边长为a的正三角形的边心距、半径（外接圆的半径）和高之比为_________________.
15.要用圆形铁片截出边长为4cm的正方形铁片，则选用的圆形铁片的直径最小要__________cm.
16.若正多边形的边心距与边长的比为1:2，则这个正多边形的边数是__________.
17.一个正三角形和一个正六边形的周长相等，则它们的面积比为__________.
第18题
18.(2013•徐州)如图，在正八边形ABCDEFGH中，四
边形BCFG的面积为20cm2，则正八边形的面积为
________cm2.
三、解答题
19.比较正五边形与正六边形，可以发现它们的相同点与不同点.
正五边形 正六边形
例如 它们的一个相同点：正五边形的各边相等，正六边形的各边也相等.
它们的一个不同点：正五边形不是中心对称图形，正六边形是中心对称图形.请你再写出它们的两个相同点和不同点.
相同点：（1）____________________________________________________________________;
（2）___________________________________________________________________.
不同点：（1）____________________________________________________________________;
（2）____________________________________________________________________.
第20题
20.已知，如图，正六边形ABCDEF的边长为6cm，求这个正六边形的外接圆半径R、边心距r6、面积S6.
第21题
21.如图，⊙O的半径为，⊙O的内接一个正多边形，边心距为1，求它的中心角、边长、面积.
22.已知⊙O和⊙O上的一点A.
（1）作⊙O的内接正方形ABCD和内接正六边形AEFCGH；
（2）在（1）题的作图中，如果点E在弧AD上，求证：DE是⊙O内接正十二边形的一边.
第22题
23.如图1、图2、图3、…、图n，M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点，且BM=CN，连结OM、ON.
(1)求图1中∠MON的度数；
(2)图2中∠MON的度数是_________，图3中∠MON的度数是_________；
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
24.3 正多边形和圆
知识点
1.各边 各角
2.正多边形 正多边形每一边所对的圆心角
3.圆心 半径 圆心角 距离
4.
5.n 轴对称图形
一、选择题
1.C 2.B 3.B 4.C 5.B 6.C
7.B
解：根据圆内接正多边形的性质可知，只要把此正六边形再化为正多边形即可，即让周角除以30的倍数就可以解决问题．
360÷30=12；
360÷60=6；
360÷90=4；
360÷120=3；
360÷180=2．
因此n的所有可能的值共五种情况，
故选B．
8.D
二、填空题
9. 10.144 11.4cm 12.12 13.45° 14.1:2:3 15. 16.四 17.2:3
18.40
三、解答题
19.相同点：（1）每个内角都相等（或每个外角都相等或对角线都相等）；
（2）都是轴对称图形（或都有外接圆和内切圆）.
不同点：（1）正五边形的每个内角是108°，正六边形的每个内角是120°；
（2）正五边形的对称轴是5条，正六边形的对称轴是6条.
20.
21.
解：连结OB
∵在Rt△AOC中，AC==1
∴AC=OC ∴∠AOC=∠OAC=45°
∵OA=OB OC⊥AB
∴AB=2AC=2 ∠AOB=2∠OAC=2×45°=90°
∴这个内接正多边形是正方形.
∴面积为22=4
∴中心角为90°，边长为2，面积为4.
第22题
22. (1)作法：
①作直径AC;
②作直径BD⊥AC;
③依次连结A、B、C、D四点,
四边形ABCD即为⊙O的内接正方形;
④分别以A、C为圆心，以OA长为半径作弧，交⊙O于E、H、F、G;
⑤顺次连结A、E、F、C、G、H各点.
六边形AEFCGH即为⊙O的内接正六边形.
(2)证明：连结OE、DE.
∵∠AOD＝＝90°，∠AOE＝＝60°，
∴∠DOE＝∠AOD－∠AOE＝90°-60°=30°.
∴DE为⊙O的内接正十二边形的一边.
23.(1)方法一：连结OB、OC.
∵正△ABC内接于⊙O，
∴∠OBM=∠OCN＝30°，
∠BOC=120°.
又∵BM=CN，OB=OC，
∴△OBM≌△OCN（SAS）.
∴∠BOM＝∠CON.
∴∠MON=∠BOC=120°.
方法二：连结OA、OB.
∵正△ABC内接于⊙O，
∴AB=AC，∠OAM=∠OBN=30°,
∠AOB=120°.
又∵BM＝CN，
∴AM=BN.
又∵OA=OB,
∴△AOM≌△BON（SAS）.
∴∠AOM=∠BON.
∴∠MON=∠AOB=120°.
(2)90° 72°
(3)∠MON=.

A．
：3
B．
：2
C．
1：2
D．
：2