

湖南省长沙市雅礼中学2022届高三下学期月考(九)数学试题-
展开绝密★启用前
湖南省长沙市雅礼中学2022届高三下学期月考(九)数学试题
试卷副标题
考试范围:xxx;考试时间:100分钟;命题人:xxx
题号
一
二
三
四
五
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
评卷人
得分
一、单选题
1.已知复数(为虚数单位),则( )
A. B. C. D.
2.已知集合,,则的子集个数为( )
A. B. C. D.
3.函数图象的大致形状为( )
A. B.
C. D.
4.《增减算法统宗》中,许多数学问题都是以歌诀的形式出现的.其中有一首“葛藤缠木”,大意是说:有根高2丈的圆木柱,该圆木的周长为3尺,有根葛藤从圆木的根部向上生长,缓慢地自下而上均匀绕该圆木7周,刚好长的和圆木一样高.已知1丈等于10尺,则能推算出该葛长为( )
A.21尺 B.25 C.29尺 D.33尺
5.“x,y为无理数”是“xy为无理数”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
6.下列对不等关系的判断,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
7.已知双曲线的右焦点为,圆(为双曲线的半焦距)与双曲线的一条渐近线交于两点,且线段的中点落在另一条渐近线上,则双曲线的方程是
A. B.
C. D.
8.若不等式在区间内的解集中有且仅有三个整数,则实数的取值范围是( ).
A. B. C. D.
评卷人
得分
二、多选题
9.如果,,都是非零向量.下列判断正确的有( )
A.若,,则 B.若,则
C.若,则 D.若,则
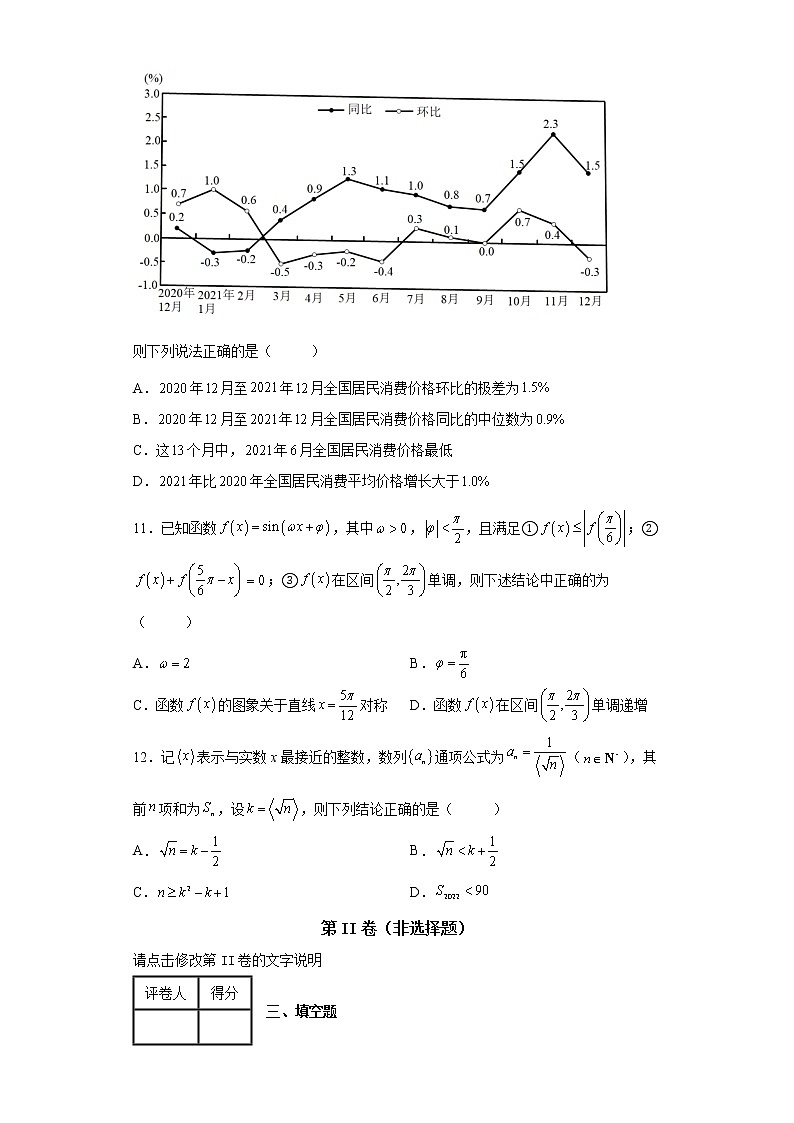
10.如图是国家统计局发布的年月至年月的全国居民消费价格涨跌幅,其中同比,环比.
则下列说法正确的是( )
A.年月至年月全国居民消费价格环比的极差为
B.年月至年月全国居民消费价格同比的中位数为
C.这个月中,年月全国居民消费价格最低
D.年比年全国居民消费平均价格增长大于
11.已知函数,其中,,且满足①;②;③在区间单调,则下述结论中正确的为( )
A. B.
C.函数的图象关于直线对称 D.函数在区间单调递增
12.记表示与实数x最接近的整数,数列通项公式为(),其前项和为,设,则下列结论正确的是( )
A. B.
C. D.
第II卷(非选择题)
请点击修改第II卷的文字说明
评卷人
得分
三、填空题
13.的展开式中,的系数为___________.(用数字作答)
14.年北京冬奥会参加冰壶混双比赛的队伍共有支,冬奥会冰壶比赛的赛程安排如下,先进行循环赛,循环赛的规则规定:每支队伍都要和其余支队伍轮流交手一次,循环赛结束后按照比赛规则决出前名进行半决赛.胜者决冠军,负者争铜牌,则整个冰壶混双比赛的场数是___________.
15.在△ABC中,,将△ABC绕BC旋转至△BCD的位置,使得,如图所示,则三棱锥外接球的体积为_____________.
评卷人
得分
四、双空题
16.椭圆的光学性质,从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上.已知椭圆:,,为其左、右焦点.是上的动点,点,若的最大值为.动直线为此椭圆的切线,右焦点关于直线的对称点,,则:(1)椭圆的离心率为___________;(2)的取值范围为___________.
评卷人
得分
五、解答题
17.在①,②是的等比中项,③这三个条件中任选一个,补充在下面问题中,并作答.
问题:已知各项均为正数的等差数列的前项和为,,且 .
(1)求;
(2)设数列的前项和为,试比较与的大小,并说明理由.
18.如图,四边形是圆柱的轴截面,圆柱的侧面积为,点在圆柱的底面圆周上,且是边长为的等边三角形,点是线段上的动点.
(1)若是的中点,求证:;
(2)若,求与平面所成角的余弦值.
19.已知等腰三角形ABC的角A,B,C所对的边分别为a,b,c,且,c(c+b)=(a+b)(a-b).
(1)求A和b;
(2)若点E,F分别是线段BC(含端点)上的动点,且BF>BE,在运动过程中始终有,求△EAF面积的最小值.
20.某校对学生关于开展数学研究性学习的态度进行调查,随机抽调了人,他们数学成绩的平均分(单位:分)的频数分布及对开展数学研究性学习赞成人数如表:
成绩
频数
赞成人数
(1)根据以上统计数据完成下面的列联表:能否有的把握认为学生关于开展数学研究性学习的态度与数学成绩平均分为分分界点有关?
成绩不低于分的人数
成绩低于分的人数
合计
赞成
不赞成
合计
(2)若对数学成绩平均分在和的被调查人中各随机选取人进行追踪调查,求在选中的人中有人不赞成的条件下,赞成开展数学研究性学习的人数的分布列及数学期望.
附参考公式与数据:,.
21.已知抛物线C:的焦点为,过且垂直于x轴的直线l与抛物线交于,两点,抛物线的准线与x轴的交点为,已知的面积为.
(1)求抛物线的方程;
(2)已知,,若在线段上,,是抛物线的两条切线,切点为,,求面积的最大值.
22.已知函数.
(1)当时,设,求的最小值;
(2)若在上恒成立,求实数的取值范围;
(3)证明:.
参考答案:
1.B
【解析】
【分析】
根据复数的除法运算求出复数,再根据复数的模的计算公式即可得解.
【详解】
解:,
所以.
故选:B.
2.C
【解析】
【分析】
化简集合A、B,再根据集合的交集运算即可.
【详解】
,,∴,∴的子集个数为8.
故选:C.
3.A
【解析】
【分析】
利用奇偶性定义判断的奇偶性,结合的符号,应用排除法确定答案.
【详解】
由且定义域为R,
所以为偶函数,排除C、D;
,且,,即,排除B.
故选:A
4.C
【解析】
【分析】
根据葛藤绕圆柱7周,由7个圆柱的侧面展开图拼成的矩形的对角线求解.
【详解】
如图所示,圆柱的侧面展开图是矩形ABEF,
由题意得:2丈=20尺,圆周长BE=3尺,
则葛藤绕圆柱7周后长为尺,
故选:C
5.D
【解析】
【分析】
对充分性和必要性分别取特殊值进行否定即可.
【详解】
充分性:取符合“x,y为无理数”,但是不符合“xy为无理数”,故充分性不满足;
必要性:当“xy为无理数”时,可以取,但是不符合“x,y为无理数”,故必要性不满足.
故“x,y为无理数”是“xy为无理数”的既不充分也不必要条件.
故选:D
6.C
【解析】
【分析】
根据不等式的性质,对数函数、指数函数、正切函数的性质判断,错误的可举反例.
【详解】
A.满足,但,A错;
B.,,满足,但,B错;
C.,C正确;
D.,但,D错.
故选:C.
【点睛】
本题考查不等式的性质,考查函数的单调性.解题关键是掌握不等式的性质,掌握指数函数、对数函数、正切函数的性质.特别是函数的单调性问题,一般只有两个在同一单调区间的自变量的值,才能比较它们函数的大小,否则需要转化为同一单调上来,否则会出错,因此可举反例说明不等式是错误的.
7.D
【解析】
渐近线过圆心,代入求出渐近线,点在圆上,得,由中点及线段的中点,由中位线得渐近线与平行,建立方程组求解.
【详解】
不妨设双曲线的一条渐近线方程为,代入圆,得,则,所以.易知点在圆上,所以,得,即①.因为线段的中点落在另一条渐近线上,且,所以,与该渐近线垂直,所以该渐近线与平行,得②.解①②组成的方程组,得,所以双曲线的方程为.
故选:D.
【点睛】
本题考查利用双曲线的几何性质求双曲线方程.
求双曲线方程的思路:
(1)如果已知双曲线的中心在原点,且确定了焦点在轴上或轴上,则设出相应形式的标准方程,然后根据条件确定关于的方程组,解出,从而写出双曲线的标准方程(求得的方程可能是一个,也有可能是两个,注意合理取舍,但不要漏解).
(2)当焦点位置不确定时,有两种方法来解决:一种是分类讨论,注意考虑要全面;另一种是设双曲线的一般方程为求解.
8.C
【解析】
【分析】
令,根据导数判断出的单调性并求得最值,根据在区间内的解集中有且仅有三个整数,转为在区间内的解集中有且仅有三个整数,结合图像可得结果.
【详解】
不等式,即,不等式成立则,
令,则.
令,得或;,得,
在和上单调递增,在上单调递减,
,且.如图所示
当时,至多有一个整数解.当时,在区间内的解集中有且仅有三个整数,只需,即,
解得.
故选:C
【点睛】
本题考查不等式的解法和应用问题,考查利用导数研究函数的单调性最值和函数图像,考查数形结合思想的应用,属于中档题.
9.ACD
【解析】
【分析】
利用平行向量的定义可判断AD,利用数量积的概念及性质可判断BC.
【详解】
∵,,都是非零向量,
∴若,,则,故A正确;
若,,则,但不一定等于,故B错误;
由,可得,整理可得,所以,故C正确;
若,则,故D正确.
故选:ACD.
10.AB
【解析】
【分析】
计算出年月至年月全国居民消费价格环比的极差,可判断A选项;利用中位数的定义可判断B选项;根据涨幅可判断C选项;利用平均数公式可判断D选项.
【详解】
年月至年月全国居民消费价格环比的最大值为,最小值为,
所以其极差为,A项正确;
年月至年月全国居民消费价格同比(单位:)从小到大依次为
、、、、、、、、、、、、,
其中位数为,B项正确;
从环比来看,假设2020年全国居民消费平均价格为1,经计算可得2020年12月全国居民消费平均价格,C项错误;
年比年全国居民消费价格平均增长为
,D项错误.
故选:AB.
11.AB
【解析】
【分析】
由①可得在处取得最值,由②可得关于对称,由③可得,结合①②与题设条件可得,进而判断选项
【详解】
由得:,;
由得:,;
∴,.
由在区间单调得:,,
又,综上可得,,,故AB正确;
又函数的图象关于点对称,满足在区间单调递减.
故CD错误;
故选:AB
12.BCD
【解析】
【分析】
A特殊值判断即可;B、C由题设可得即可判断正误;D通过归纳总结得到数列中有2个1,4个,6个,8个,……,根据中各对应值的项数,进而求和.
【详解】
由题意,记表示与实数最接近的整数且,
当时,可得,则, A不正确;
由,即,可得,故成立, B正确;
由B分析知:,平方得:,
因为且不是整数,其中是右侧的最接近的整数,所以成立, C正确;
当时,,此时;
当时,,此时;
当时,,此时;
当时,,此时;……
归纳得:数列中有2个1,4个,6个,8个,……
又2,4,6,8,…构成首项为2,公差为2的等差数列,其前项和,
而,所以, D正确.
故选:BCD
【点睛】
关键点点睛:D选项,首先通过列举归纳总结出对应值出现的次数,再由等差数列前n项和公式确定项的分布情况,进而求出.
13.5
【解析】
【分析】
利用二项展开式的通项公式可求得结果.
【详解】
的展开式的通项公式为,,
令,得,
所以的系数为.
故答案为:5
14.49
【解析】
【分析】
分别计算循环赛、半决赛、决赛和铜牌争夺赛的场次再求和即可
【详解】
循环赛有场,决出前4名后,分两组进行半决赛,半决赛举行2场,胜者决冠军举行1场,负者争铜牌举行1场,共举行场.
故答案为:49
15.
【解析】
【分析】
在△ABC中,利用余弦定理求得,从而将三棱锥D—ABC放入长方体中,如图所示,设长方体的长、宽、高分别为a,b,c,则,长方体的外接球半径就是三棱锥D—ABC的外接球半径,求出长方体的对角线,可求得外接球的半径,从而可求出体积
【详解】
在△ABC中,由余弦定理得,所以.
在三棱锥D—ABC中,.
将三棱锥D—ABC放入长方体,设长方体的长、宽、高分别为a,b,c,
棱锥D—ABC外接球的半径为R,则,
所以,
所以,
从而三棱锥D—ABC外接球的体积
故答案为:
16.
【解析】
【分析】
根据题意得,所以,求出,即可求出,再求出离心率;根据椭圆的光学性质可得,即点的轨迹是以为圆心,半径为4的圆,又表示点到直线的距离的倍,分析求解即可.
【详解】
根据椭圆定义得:,
所以,因为的最大值为6,
因为,所以,即,解得,所以离心率为.
右焦点关于直线的对称点,设切点为,由椭圆的光学性质可得:
,,三点共线,所以,
即点的轨迹是以为圆心,半径为4的圆,
圆心到直线的距离为,
则圆上的点到直线的距离最小值,最大值,
所以点到直线的距离为:,
所以表示点到直线的距离的倍,
则,即.
故答案为:,.
17.(1)(2),理由见解析
【解析】
【分析】
(1)设等差数列{an}的公差为d,根据所选条件求出数列{an}的首项和公差,进一步求出{an}的通项公式;
(2)求得,运用数列的裂项相消求和求得,将与作差,通分化简可得大小.
【详解】
设等差数列的公差为,则
,
.
方案一:选条件①
由,
解得,,
.
又
方案二:选条件②
由
解得,
同方案一
方案三:选条件③
由
解得,
同方案一
【点睛】
规律方法点睛:使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点.
18.(1)证明见解析
(2)
【解析】
【分析】
(1)先证明出BP⊥AG,DP⊥AG,利用线面垂直的判定定理证明出AG⊥面BPD,即可证明AG⊥BD;
(2)在底面内过O作,连结OQ.以O为原点,分别为x、y、z轴正方向建立空间直角坐标系.用向量法求解.
(1)
设圆柱的底面半径为,高为.
因为三角形是边长为的等边三角形,所以.
因为圆柱的侧面积为,所以,解得:.
在底面圆中,,,所以.
因为圆柱的母线底面,所以,.
因为,
所以,又,所以面.
因为面,
所以.在三角形中,,是的中点,所以.
又,所以面.
因为面,所以.
(2)
在底面内过作,连接.以为原点,,,分别为,,轴正方向建立空间直角坐标系.
则,,,,,,.
所以,,.
因为,,
.
设为平面的法向量,
则,即,令得.
设与平面所成角为,则.
∵,∴与平面所成角的余弦值为.
19.(1)
(2)
【解析】
【分析】
(1)利用正弦定理结论,结合,可求得;利用余弦定理结合即可求得A,从而求得b.
(2)利用(1)中的结论,分别在三角形和三角形中利用正弦定理,结合三角形面积公式,即可解出答案.
(1)
由正弦定理得:即: (R为三角形ABC的外接圆半径),
故 ,
由 得: ,
则 ,因为 ,故 ;
由等腰三角形ABC可得 ,故 ;
(2)
由(1)知: ,
由点E,F分别是线段BC(含端点)上的动点,且BF>BE,在运动过程中始终有 ,
知点在点的左边,如图:
设 ,不变,可知,
在中,由正弦定理可得,
,
在中,由正弦定理可得,
,
故
,,
,
三角形的面积的最小值为,此时.
20.(1)表格见解析,有;(2)分布列见解析,.
【解析】
【分析】
(1)根据频数分布表中的数据填写列联表,再利用求出,然后利用临界值表进行判断,
(2)由题意知,的所有可能取值为,,,,然后求出各自对应的概率,从而可列出分布列,求出数学期望
【详解】
解:(1)根据统计数据填写列联表,如下:
成绩不低于分的人数
成绩低于分的人数
合计
赞成
不赞成
合计
40
50
由表中数据,计算,
所以有的把握认为学生关于开展数学研究性学习的态度与数学成绩平均分为分分界点有关;
(2)由题意知,的所有可能取值为,,,,则
,
,
,
,
所以的分布列为:
数学期望为.
21.(1)
(2)
【解析】
【分析】
(1)联立准线与抛物线的方程可得,,再根据面积求解即可;
(2)设,,的方程为,联立抛物线的方程,根据判别式为0可得切线的方程为:,同理得到切线的方程,再根据点在切线、上,进而得直线的方程,联立抛物线的方程并表达出面积,结合韦达定理化简求解即可
(1)
抛物线的焦点为,准线为:,直线为:,点,联立,解得:,或,不妨设,,则.,得.
∴抛物线的方程为;
(2)
∵,,在线段上,∴,且.
依题意:切线,的斜率存在,
设,,的方程为,
联立,消去得:,
,
整理得:,解得:,
∴切线的方程为:,即:.
同理可得切线的方程为,
又点在切线、上,∴,得直线的方程为,
即.联立,得,
∴.
又点到直线的距离,
∴.
∵,∴,,则.
即面积的最大值为.
22.(1)
(2)
(3)证明见解析
【解析】
【分析】
(1)根据题意,所以,得在上恒成立,即在上单调递增,所以,即在上单调递增,求解即可;(2)根据题意得当时,恒成立,设,所以,再设,所以,可以求出的单调性,进而得到在上存在唯一零点,设为,确定的单调性,求出的最小值即可;(3)根据题意得,构造,求解证明即可.
(1)
根据题意,函数,所以,
则,故在上恒成立,
所以在上单调递增,则有,所以在上单调递增,
则有,故的最小值为;
(2)
根据题意得:在上恒成立,
当时,;当时,,设,
,
设,,
则时,,单调递增;时,,
单调递减.而,,,
所以在上存在唯一零点,设为,则时,,;
时,,,所以在处取得最大值,
在处取得最小值,所以,综上所述:实数的取值范围为.
(3)
由(2)知:时,,所以,所以,
即,
所以
,
所以.
【点睛】
函数的单调性是函数的重要性质之一,它的应用贯穿于整个高中数学的教学之中.某些数学问题从表面上看似乎与函数的单调性无关,但如果我们能挖掘其内在联系,抓住其本质,那么运用函数的单调性解题,能起到化难为易、化繁为简的作用.因此对函数的单调性进行全面、准确的认识,并掌握好使用的技巧和方法,这是非常必要的.根据题目的特点,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这种思想去解决,往往能获得简洁明快的思路,有着非凡的功效.
湖南省长沙市雅礼中学2023届高三下学期月考(八)数学试题: 这是一份湖南省长沙市雅礼中学2023届高三下学期月考(八)数学试题,文件包含数学答案pdf、湖南省长沙市雅礼中学2023届高三月考八数学试卷pdf等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。
精品解析:湖南省长沙市雅礼中学2023届高三下学期月考(七)数学试题: 这是一份精品解析:湖南省长沙市雅礼中学2023届高三下学期月考(七)数学试题,文件包含精品解析湖南省长沙市雅礼中学2023届高三下学期月考七数学试题解析版docx、精品解析湖南省长沙市雅礼中学2023届高三下学期月考七数学试题原卷版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。
2022届湖南省长沙市雅礼中学高三下学期月考(八)数学试题(解析版): 这是一份2022届湖南省长沙市雅礼中学高三下学期月考(八)数学试题(解析版),共21页。试卷主要包含了单选题,多选题,填空题,双空题,解答题等内容,欢迎下载使用。












