高中数学人教B版 (2019)必修 第一册3.1.2 函数的单调性教案

   第三章  函数

3.1.2 函数的单调性教学设计

教材分析：

函数的单调性与最值指的是在初中的基础上对函数的单调性的再认识，是利用集合与对应的思想来理解函数的定义，从而加深对抽象函数单调性的定义理解，根据定义证明函数的单调性，理解单调区间以及理解函数最大（小）值的定义并掌握其求法。由于它还是初等数学和高等数学衔接的枢纽，所以在本学科有不可替代的重要位置的地位，是本学科的核心内容。教学的重点是掌握利用函数图象和单调性定义判断、证明函数的单调性，理解单调区间以及理解函数最大（小）值的定义并掌握其求法。函数的单调性与最值指的是在初中的基础上对函数的单调性的再认识，是利用集合与对应的思想来理解函数的定义，从而加深对抽象函数单调性的定义理解，根据定义证明函数的单调性，理解单调区间以及理解函数最大（小）值的定义并掌握其求法。由于它还是初等数学和高等数学衔接的枢纽，所以在本学科有不可替代的重要位置的地位，是本学科的核心内容。教学的重点是掌握利用函数图象和单调性定义判断、证明函数的单调性，理解单调区间以及理解函数最大（小）值的定义并掌握其求法。

教学目标：

会用三种语言表述函数单调性；掌握用定义证明函数单调性的基本方法和步骤。

在函数单调性的研究中，让学生经历观察分析、归纳概括、语言表示的思维过程，初步体会研究函数性质的方法。培养函数思维能力。

通过单调性的学习树立善于思考、敢于质疑、严谨求实的精神。

初步感知平均变化率与函数增长速度之间的关系，培养数学抽象、直观想象、数学运算、逻辑推理等数学素养．

【教学重点】

1.函数单调性的判定与证明

2.求函数的单调区间

3.用图像法、函数的单调性求函数的最值.

4.函数最值的应用问题

【教学难点】

1.利用单调性证明一些简单的不等式

2.对抽象函数的单调性判断

3.借助函数单调性求最值

在函数的单调性的教学中，准备使用《几何画板》。因为使用《几何画板》，有利于规范作图。

教学过程

一、单调性的定义与证明

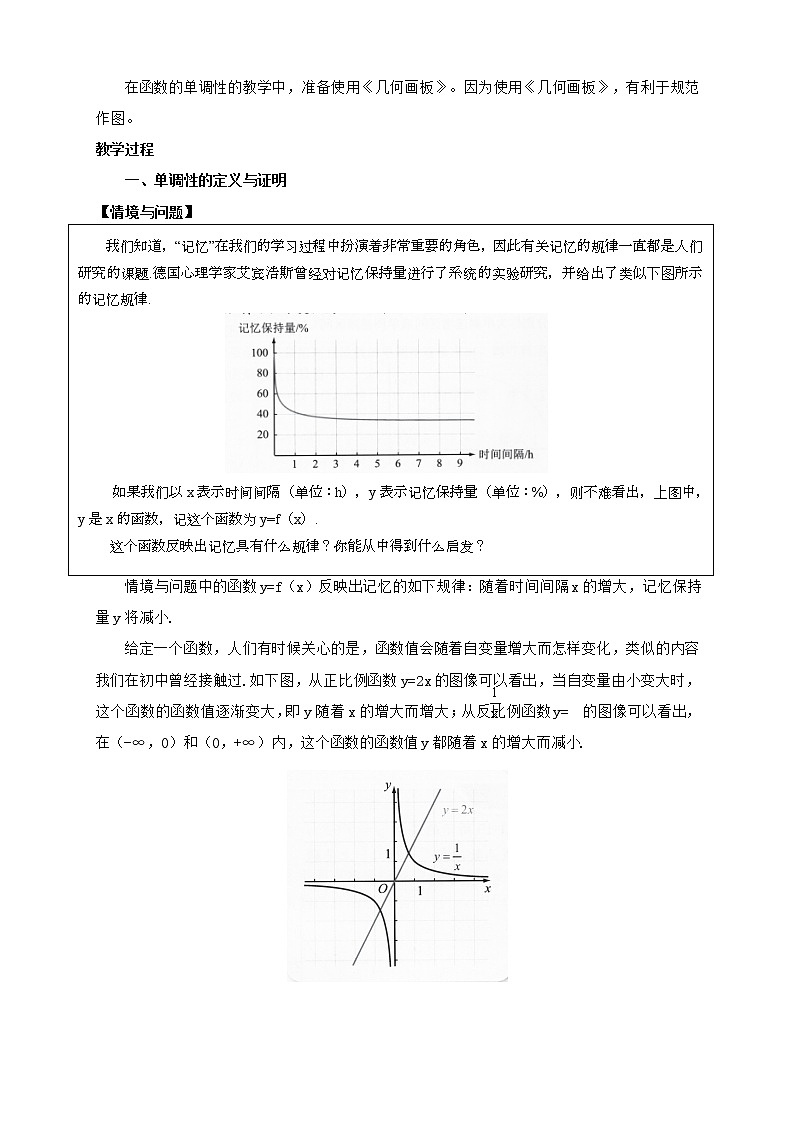
【情境与问题】

情境与问题中的函数y=f（x）反映出记忆的如下规律：随着时间间隔x的增大，记忆保持量y将减小.

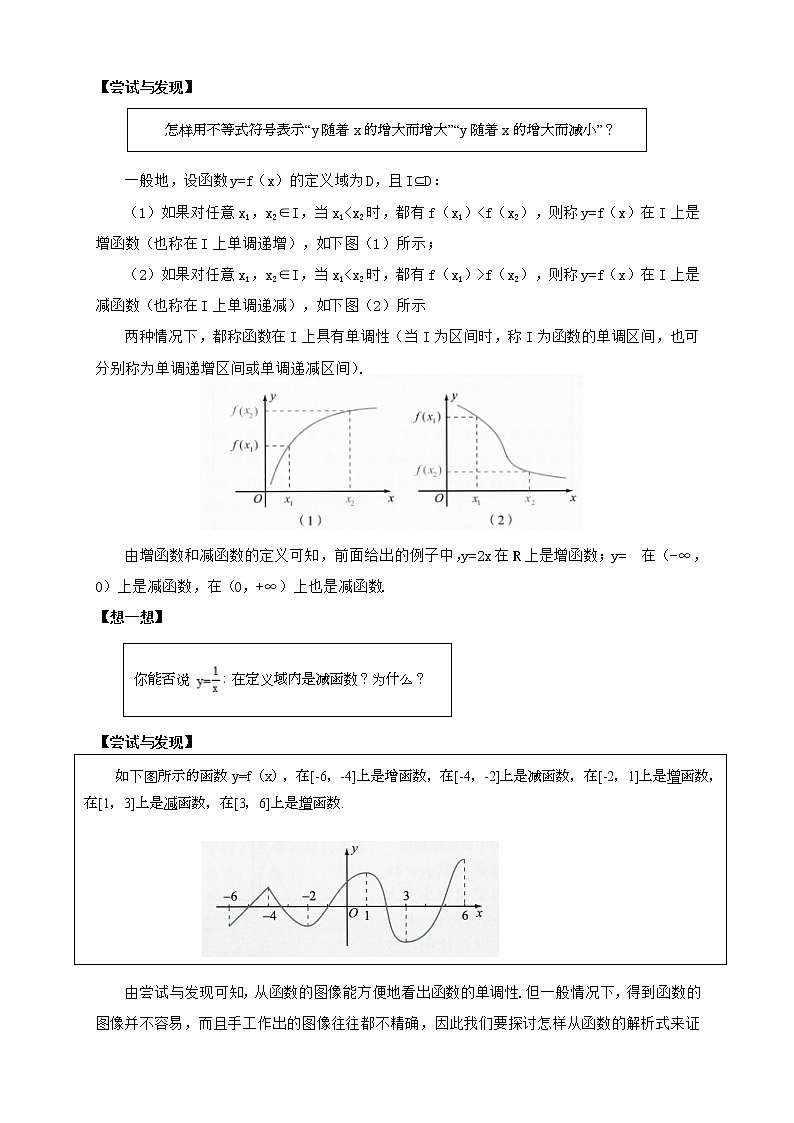
给定一个函数，人们有时候关心的是，函数值会随着自变量增大而怎样变化，类似的内容我们在初中曾经接触过.如下图，从正比例函数y=2x的图像可以看出，当自变量由小变大时，这个函数的函数值逐渐变大，即y随着x的增大而增大；从反比例函数y=  的图像可以看出，在（-∞，0）和（0，+∞）内，这个函数的函数值y都随着x的增大而减小.

【尝试与发现】

一般地，设函数y=f（x）的定义域为D，且I⊆D：

（1）如果对任意x1，x2∈I，当x1<x2时，都有f（x1）<f（x2），则称y=f（x）在I上是增函数（也称在I上单调递增），如下图（1）所示；

（2）如果对任意x1，x2∈I，当x1<x2时，都有f（x1）>f（x2），则称y=f（x）在I上是减函数（也称在I上单调递减），如下图（2）所示

两种情况下，都称函数在I上具有单调性（当I为区间时，称I为函数的单调区间，也可分别称为单调递增区间或单调递减区间）.

由增函数和减函数的定义可知，前面给出的例子中，y=2x在R上是增函数；y=  在（-∞，0）上是减函数，在（0，+∞）上也是减函数.

【想一想】

【尝试与发现】

由尝试与发现可知，从函数的图像能方便地看出函数的单调性.但一般情况下，得到函数的图像并不容易，而且手工作出的图像往往都不精确，因此我们要探讨怎样从函数的解析式来证明函数的单调性.这可以利用函数单调性的定义和不等式的证明方法.

【典型例题】

例1 求证：函数f（x）=-2x在R上是减函数.

证明 任取x1，x2∈R且x1<x2，则x1-x2<0，那么

f（x1）-f（x2）=（-2x1）-（-2x2）=2（x2-x1）>0，

从而f（x1）>f（x2）.

因此，函数f（x）=-2x在R上是减函数.

一般地，设函数f（x）的定义域为D，且x0∈D：如果对任意x∈D，都有f（x）≤f（x0），则称f（x）的最大值为f（x0），而x0称为f（x）的最大值点；如果对任意x∈D，都有f（x）≥f（x0），则称f（x）的最小值为f（x0），而x0称为f（x）的最小值点.最大值和最小值统称为最值，最大值点和最小值点统称为最值点.

不难看出，如果函数有最值而且函数的单调性容易求出，则可利用函数的单调性求出函数的最值点和最值

例2 判断函数f（x）=3x+5，x∈[-1，6]的单调性，并求这个函数的最值.

解   任取x1，x2∈[-1，6]且x1<x2，则x1-x2<0，那么

f（x1）-f（x2）=（3x1+5）-（3x2+5）=3（x1-x2）<0，

所以这个函数是增函数.

因此，当-1≤x≤6时，有

f（-1）≤f（x）≤f（6），

从而这个函数的最小值为f（-1）=2，最大值为f（6）=23.

例2的结论也可由不等式的知识得到：因为-1≤x≤6，所以

-3≤3x≤18，2≤3x+5≤23，

即f（-1）≤f（x）≤f（6），其余同上.

二、函数的平均变化率

我们已经知道，两点确定一条直线，在平面直角坐标系中，这一结论当然也成立.一般地，给定平面直角坐标系中的任意两点A（x1，y1），B（x2，y2），当x1≠x2时，称

为直线AB的斜率；当x1=x2时，称直线AB的斜率不存在.

直线AB的斜率反映了直线相对于x轴的倾斜程度.

若记Δx=x2一x1，相应的Δy=y2-y1，则当Δx≠0时，斜率可记为解为

如下图所示，直线AB的斜率即为Rt△ACB中BC与AC的比.另外，图中，直线AB的斜率大于零，而直线AD的斜率小于零.

不难看出，平面直角坐标系中的三个点共线，当且仅当其中任意两点确定的直线的斜率都相等或都不存在.下面我们用直线的斜率来研究函数的单调性.

由函数的定义可知，任何一个函数图像上的两个点，它们所确定的直线的斜率一定存在.

【尝试与发现】

可以看出，函数递增的充要条件是其图像上任意两点连线的斜率都大于0，函数递减的充要条件是其图像上任意两点连线的斜率都小于0

一般地，若I是函 数y=f（x）的定义域的子集，对任意x1，x2∈I且x1≠x2，记y1=f（x1），y2=f（x2 ），            （即                 ），则：

（1）y=f（x）在I上是增函数的充要条件是       在I上恒成立；

（2）y=f（x）在I上是减函数的充要条件是       在I上恒成立。

一般地，当x1≠x2时，称

为函数y=f（x）在区间[x1，x2]（x1<x2时）或[x2，x1]（x1>x2时）上的平均变化率。

利用上述结论，我们可以证明一个函数的单调性.

例如，对于函数y=-2x来说，对任意x1，x2∈R且x1≠x2，有

因此y=-2x在R上是减函数.

【拓展阅读】

【典型例题】

例3   求证：函数y=   在区间（-∞，0）和（0，+∞）上都是减函数

证明  设x1≠x2，那么

如果x1，x2∈（-∞，0），则x1x2>0，此时   ＜0，所以函数在（-∞，0）上是减函数.同理，函数在（0，+∞）也是减函数

例4  判断一次函数y=kx+b（k≠0）的单调性.

解  设x1≠x2，那么

因此，一次函数的单调性取决于k的符号：当k>0时，一次函数在R上是增函数；当k<0时，一次函数在R上是减函数.

例4说明，一次函数y=kx+b（k≠0）的图像上任意两点确定的直线斜率均为k，这实际上也说明了一次函数的图像一定是直线不仅则此，此时从   =k还可以看出，Δy=kΔx，这就意味着在一次函数中，Δy与Δx成正比，且比例系数为k.特别地，当自变量每增大一个单位时，因变量增大k个单位，而且可以证明，只有一次函数才具有这个性质.事实上，如果Δy=kΔx，设x=0时函数值为y0，则

y-y0=k（x-0），

即y=kx+y0，因此一定是一次函数.正因为如此，一次函数也经常被称为线性函数.

例如，如果向给定的容器中倒水，且任意相等的时间间隔内所倒的水体积相等，那么容器内水面的高度y是时间t的函数。

当容器是下图（1）所示的圆柱时，在固定的Δt时间内，Δy应该是常数，因此函数的图像是如下图（2）所示的一条线段.

当容器是如下图（1）所示圆台时，由容器的形状可知，在固定的Δt时间内，随着t的增加，Δy应该越大，因此函数的图像如图（2）所示。

【典型例题】

例5  证明函数f（x）=x2+2x在（-∞，-1]上是减函数，在[-1，+∞）上是增函数，并求这个函数的最值.

当然，这一结论也可以从二次函数的图像是关于x=     对称的抛物线与开口方向看出来.

【拓展与阅读】

教学反思

在本节课的教学中，学生可能遇到的问题是归纳抽象函数单调性的定义，并根据定义证明函数的单调性以及求一个具体函数的最值。产生这一问题的原因是对抽象函数还不熟练，对于函数单调性的定义还不是很理解，其次单调性的证明是学生在函数内容中首次接触到的代数论证内容，而学生在代数方面的推理论证能力是比较薄弱的。要解决这一问题，就要加强对函数单调性的理解，通过对证明过程的分析，帮助学生掌握单调性的证明，以及求函数的最值。