苏科版九年级下册第8章 统计和概率的简单应用8.2 货比三家优秀习题

这是一份苏科版九年级下册第8章 统计和概率的简单应用8.2 货比三家优秀习题，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

8.2货比三家苏科版初中数学九年级下册同步练习
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）

一、选择题（本大题共12小题，共36.0分）
1. 某学校为了加强学生的安全意识，组织学生观看了纪实片《孩子，请不要私自下水》，并对部分学生进行调查．根据下面两幅不完整的统计图可以求出，在这次调查中被调查的学生有(    )

A. 400名 B. 380名 C. 350名 D. 300名
2. 某班有48位同学，在一次数学检测中，分数只取整数，统计其成绩，绘制出频数分布直方图(横半轴表示分数，把50.5分到100.5分之间的分数分成5组，组距是10分，纵半轴表示频数)如图所示，从左到右的小矩形的高度比是1：3：6：4：2，则由图可知，其中分数在70.5～80.5之间的人数是(    )

A. 9 B. 18 C. 12 D. 6
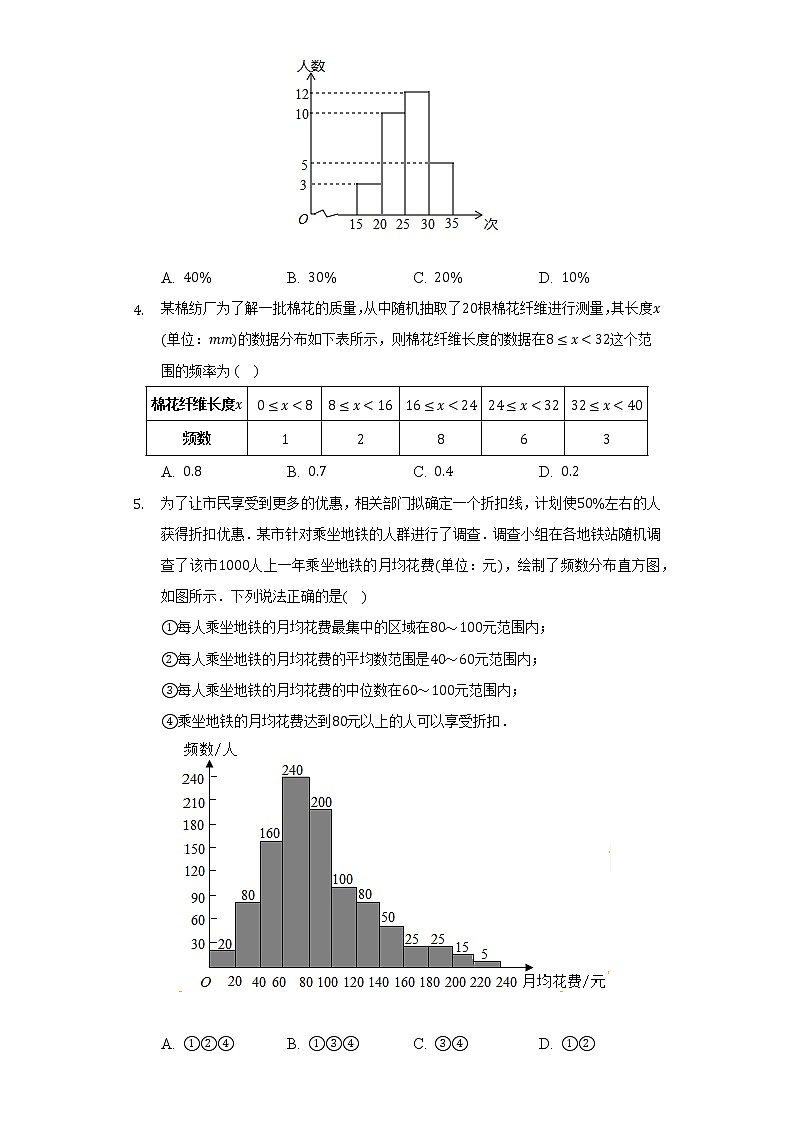
3. 为了了解某校九年级学生的体能情况，随机抽查了该校九年级若干名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的直方图，请根据图示计算，仰卧起坐次数在25～30次的学生人数占被调查学生人数的百分比为(    )

A. 40% B. 30% C. 20% D. 10%
4. 某棉纺厂为了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x(单位：mm)的数据分布如下表所示，则棉花纤维长度的数据在8≤x<32这个范围的频率为(    )
棉花纤维长度x
0≤x<8
8≤x<16
16≤x<24
24≤x<32
32≤x<40
频数
1
2
8
6
3
A. 0.8 B. 0.7 C. 0.4 D. 0.2
5. 为了让市民享受到更多的优惠，相关部门拟确定一个折扣线，计划使50%左右的人获得折扣优惠．某市针对乘坐地铁的人群进行了调查．调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位：元)，绘制了频数分布直方图，如图所示．下列说法正确的是(    )
①每人乘坐地铁的月均花费最集中的区域在80～100元范围内；
②每人乘坐地铁的月均花费的平均数范围是40～60元范围内；
③每人乘坐地铁的月均花费的中位数在60～100元范围内；
④乘坐地铁的月均花费达到80元以上的人可以享受折扣．

A. ①②④ B. ①③④ C. ③④ D. ①②
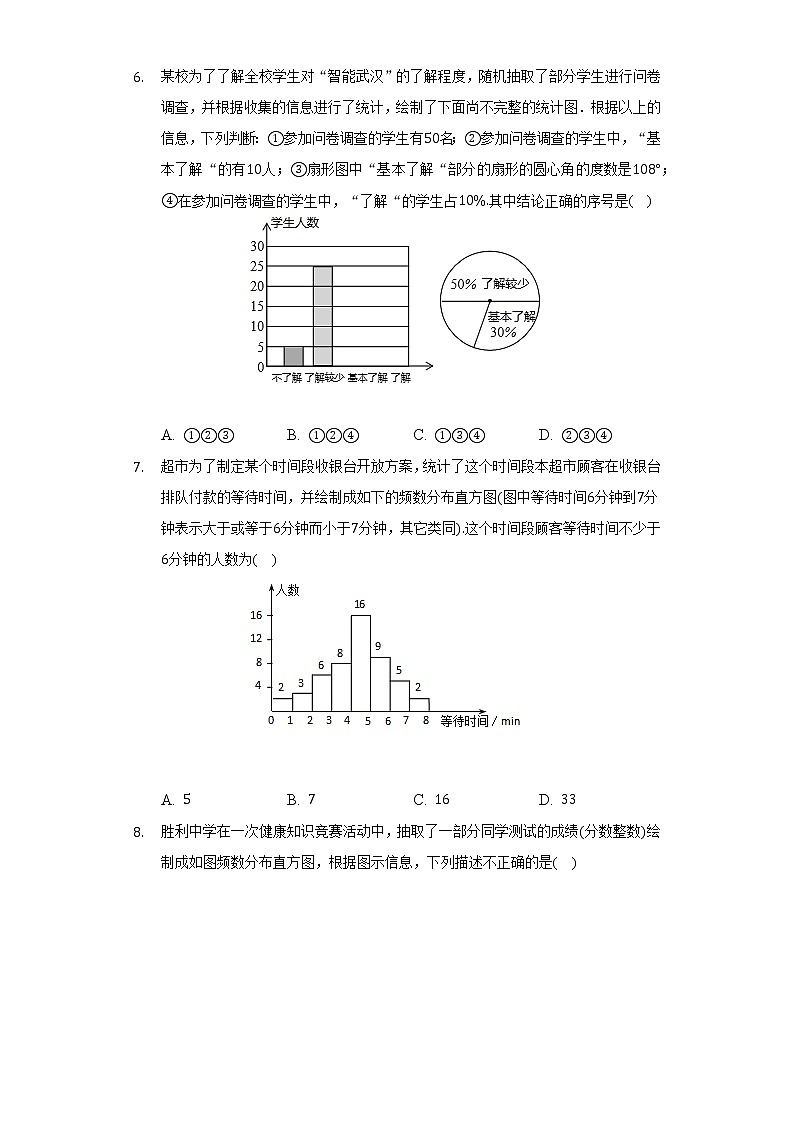
6. 某校为了了解全校学生对“智能武汉”的了解程度，随机抽取了部分学生进行问卷调查，并根据收集的信息进行了统计，绘制了下面尚不完整的统计图．根据以上的信息，下列判断：①参加问卷调查的学生有50名；②参加问卷调查的学生中，“基本了解“的有10人；③扇形图中“基本了解“部分的扇形的圆心角的度数是108°；④在参加问卷调查的学生中，“了解“的学生占10%.其中结论正确的序号是(    )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
7. 超市为了制定某个时间段收银台开放方案，统计了这个时间段本超市顾客在收银台排队付款的等待时间，并绘制成如下的频数分布直方图(图中等待时间6分钟到7分钟表示大于或等于6分钟而小于7分钟，其它类同).这个时间段顾客等待时间不少于6分钟的人数为(    )

A. 5 B. 7 C. 16 D. 33
8. 胜利中学在一次健康知识竞赛活动中，抽取了一部分同学测试的成绩(分数整数)绘制成如图频数分布直方图，根据图示信息，下列描述不正确的是(    )

A. 抽查了50个学生
B. 成绩在60.5～70.5范围的频数为2
C. 成绩在70.5～80.5范围的频数比成绩在60.5～70.5范围的频数多1
D. 成绩在70.5～80.5范围的频率为0.8
9. 八年级期末体育测试结束后，某班体育委员将本班50名学生的测试成绩制成如下的统计表．则这个班学生体育测试成绩是优秀的频数是(分数在27分及以上为优秀)(    )
成绩(分)
20
21
22
23
24
25
26
27
28
29
30
人数(人)
1
1
2
4
5
6
5
8
10
6
2
A. 18 B. 26 C. 30 D. 34
10. 在样本容量为160的频数分布直方图中，共有3个小长方形，若中间一个小长方形的高与其余两个小长方形高的和之比是1:4，则中间一组的频率为(    )
A. 40 B. 32 C. 0.25 D. 0.2
11. 下列5个数：−π3、3−8、2、227、(−1)2021中，无理数出现的频数是(    )
A. 2 B. 3 C. 0.4 D. 0.6
12. 为了减轻学生课外作业负担，数学老师准备按照学生每天课外作业完成量(完成题目个数)实行分档布置作业．作业量分档递增，计划使第一档、第二档和第三档的作业量覆盖全校学生的70%，20%和10%，为合理确定各档之间的界限，随机抽查了该校500名学生过去一个阶段完成作业量的平均数(单位：个)；绘制了统计图．如图所示，下面四个推断合理的是(    )

A. 每天课外作业完成量不超过15个题的该校学生按第二档布置作业
B. 每天课外作业完成量超过21个的该校学生按第三档布置作业
C. 该校学生每天课外作业完成量的平均数不超过18
D. 该校学生每天课外作业完成量的中位数在15−18之间
第II卷（非选择题）

二、填空题（本大题共4小题，共12.0分）
13. 下表是某种数学报纸的销售份数x(份)与价钱y(元)的统计表，观察下表：
份数x(份)
1
2
3
4
…
收入y(元)
0.5
1.0
1.5
2.0
…
则买48份这种报纸应付______元．
14. 在一个不透明的袋子里有1个红球，2个白球和若干个黑球．小宇将袋子中的球摇匀后，从中任意摸出一个，记下颜色后放回袋中，在多次重复以上操作后，小宇统计了摸到红球的频率，并绘制了如图折线图．则从袋子中随机摸出两个球，这两个球一红一白的概率为______．
．
15. 一次数学单元测试后，全班50名学生的成绩被分成5组，第1−4组的频数分别是：18，10，12，4，则第五组的频率是______．
16. 一个容量为80的样本最大值为143，最小值为50，取组距为10，则可以分成____________组．

三、解答题（本大题共7小题，共56.0分）
17. 质检员小李对车间3月21日生产的15个零件进行了测量，所得数据整理如下表：
编号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
⑪
⑫
⑬
⑭
⑮
尺寸/mm
50.8
48.6
50.6
50.1
49.4
50.3
49.7
49.9
49.2
49.6
50.4
49.1
50.7
47.8
a

尺寸/mm
产品等次
49.7≤x≤50.3
特等品
49.5≤x≤50.5
优等品
49.0≤x≤51.0
合格品
x<49.0或x>51.0
残次品
(注：在统计优等品个数时，将特等品计算在内；在统计合格品个数时，将优等品(含特等品)计算在内．)
(1)已知这次抽检的合格率为80%，请判断编号为⑮的产品是否为合格品，并说明理由．
(2)求出此次抽检出的优等品尺寸的中位数．
(3)将这些优等品分成两组，一组尺寸大于50.0mm，另一组尺寸不大于50.0mm，从这两组中各随机抽取1件进行复检，请求出抽取到的2件产品都是特等品的概率．
18. 为了提高玉米产量进行良种优选．某农业科学院选择了两块基本条件大致相同的试验田用于分析甲、乙两种玉米种子的产量，从两块试验田中各随机抽取了20穗玉米，并对其单穗质量(单位；克)进行整理分析，过程如下：
收集数据：
甲型种子：161 161 172 181 194 201 206 206 211 215
215 222 226 232 232 232 242 246 251 254
乙型种子：162 174 183 185 196 207 208 213 215 217
219 220 220 220 225 228 236 237 245 250
整理数据：
分组
型号
160 180 200 220 240 甲
3
2
6
a
4
乙
2
3
9
4
2
分析数据：
统计量
型号
平均数
众数
中位数
方差
甲
213
m
215
759.8
乙
213
220
n
536.3
根据以上信息，回答下列问题：
(1)填空：a=______，m=______，n=______．
(2)此次调查中，单穗质量为217克的玉米在单穗质量排名(从高到低)中更靠前的是______型玉米；
(3)综合以上信息，你认为哪种玉米种子的产量表现更好，请说明理由．
19. 2021年7月24日中共中央办公厅、国务院办公厅颁布了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》，该意见对学生睡眠时间提出了新的要求．为了了解某校初二年级学生的睡眠时长，随机抽取了初二年级男生和女生各20位，对其同一天的睡眠时长进行调查，并对数据进行收集、整理、描述和分析．下面给出了相关信息．
a.睡眠时长(单位：小时)：
男生
7.7
9.9
9.8
5.5
9.6
9.6
8.6
9.8
9.9
7.9
9.0
7.5
7.7
8.5
9.2
8.7
9.2
9.3
9.2
9.4
女生
9.0
7.6
9.1
9.0
8.0
7.9
8.6
9.2
9.0
9.3
8.2
9.2
8.8
8.5
9.1
8.6
9.0
9.5
9.3
9.1
b.睡眠时长频数分布直方图(分组：5≤x<6，6≤x<7，7≤x<8，8≤x<9，9≤x<10)：
c.睡眠时长的平均数、众数、中位数如下：
年级
平均数
众数
中位数
男生
8.8
m
9.2
女生
8.8
9.0
n
根据以上信息，回答下列问题：
(1)补全男生睡眠时长频数分布直方图；
(2)直接写出表中m，n的值；
(3)根据抽样调查情况，可以推断______(填“男生”或“女生”)睡眠情况比较好，理由为______．
20. 为了解天水市民对全市创建全国文明城市工作的满意程度，某中学数学兴趣小组在某个小区内进行了调查统计．将调查结果分为不满意，一般，满意，非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图．

请结合图中的信息，解决下列问题：
(1)此次调查中接受调查的人数为______人；
(2)请你补全条形统计图；
(3)扇形统计图中“满意”部分的圆心角为______度；
(4)该兴趣小组准备从调查结果为“不满意”的4位市民中随机选择2位进行回访，已知这4位市民中有2位男性，2位女性．请用画树状图的方法求出选择回访的市民为“一男一女”的概率．
21. 为让同学们了解新冠病毒的危害及预防措施，某中学举行了“新冠病毒预防”知识竞赛．数学课外活动小组将八(1)班参加本校知识竞赛的40名同学的成绩(满分为100分，得分为正整数且无满分，最低为75分)分成五组进行统计，并绘制了下列不完整的统计图表：
分数段
频数
频率
74.5−79.5
2
0.05
79.5−84.5
8
n
84.5−89.5
12
0.3
89.5−94.5
m
0.35
94.5−99.5
4
0.1
(1)表中m=______，n=______；
(2)请补全频数分布直方图；
(3)本次知识竞赛中，成绩在94.5分以上的选手，男生和女生各占一半，从中随机确定2名学生参加颁奖，请用列表法或树状图法求恰好是一名男生和一名女生的概率．

22. 某校开展主题为“防疫常识知多少”的调查活动，抽取了部分学生进行调查，调查问卷设置了四个等级，分别是A：非常了解、B：比较了解、C：基本了解、D：不太了解，抽取了部分学生进行调查，要求每个学生填且只能填其中的一个等级，采取随机抽样的方式，并根据调查结果绘制成如图所示不完整的频数分布表和频数分布直方图，根据以上信息回答下列问题：
等级
频数
频率
A
20
0.4
B
15
b
C
10
0.2
D
a
0.1
(1)频数分布表中a=______，b=______，将频数分布直方图补充完整；
(2)若该校有学生1000人，请根据抽样调查结果估算该校A等级和B等级防疫常识的学生共有多少人？
(3)在(2)的条件下，该校为了提高学生的防疫意识，决定对C、D等级的学生进行防疫知识的普及教育，将C、D等级的学生转化为A、B等级的学生，并使普及后全校学生A等级学生人数至少是B等级学生人数的2倍，那么至少需要多少C、D等级的学生转化为A等级的学生？

23. 刚结束的体育中考中，某中学取得了优异的成绩，现随机抽查了部分同学的体育成绩，根据成绩分成如下六组：A：40≤x<45；B：45≤x<50；C：50≤x<55；D：55≤x<60；E：60≤x<65；F：65≤x≤70.并制作出如下不完整的统计图，根据统计图解决下列问题．

(1)补全频数分布直方图，并求出m的值；
(2)测试成绩不低于60分为优秀，则本次测试的优秀率是多少？
(3)现要从F组的4名同学中抽取2名同学去参加体育特训班，这4名同学恰好是两男两女，请用列表法或画树状图法，求选中的同学当中恰好是一男一女的概率．
答案和解析

1.【答案】A 
【解析】解：20÷5%=400人，
故选：A．
从两个统计图可得，“一定会”的有20人，占调查人数的5%，可求出调查人数．
考查扇形统计图、条形统计图的意义和制作方法，从两个统计图中获取数量及数量之间的关系是解决问题的关键，

2.【答案】B 
【解析】解：由图形可知，从左到右的小矩形的高度比是1：3：6：4：2，且总数为48，
所以分数在70.5～80.5之间的人数是48×61+3+6+4+2=18(人)．
故选B．
由频数分布直方图上的小长方形的高为频数，知道高度比，即可算出每组的频率，再根据数据总数，即可求出每组对应的频数．
本题主要考查学生对频数直方图的认识和对频数的计算．

3.【答案】A 
【解析】解：由频率直方图可以得出，被调查的总人数=3+10+12+5=30.又仰卧起坐次数在25～30次的学生人数为12，故百分比为40%。
根据频率直方图可以知道被调查的总人数，又在要求的范围可以很直观地由图形看出，即可得出百分比。
本题考查读频数分布直方图的能力和利用统计图获取信息的能力。利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题。

4.【答案】A 
【解析】略

5.【答案】C 
【解析】解：①根据频数分布直方图，可得众数为60−80元范围，故每人乘坐地铁的月均花费最集中的区域在60−80元范围内，故①错误；
②每人乘坐地铁的月均花费的平均数=876001000=87.6元，故每人乘坐地铁的月均花费不在40～60元范围内，故②错误；
③每人乘坐地铁的月均花费的中位数约为80元，在60～100元范围内，故③正确；
④为了让市民享受到更多的优惠，若使50%左右的人获得折扣优惠，则乘坐地铁的月均花费达到80元以上的人可以享受折扣，故④正确．
故选：C．
根据频数分布直方图中的数据，求得众数，平均数，中位数，即可得出结论．
本题主要考查了频数分布直方图，平均数以及中位数的应用，将一组数据按照从小到大(或从大到小)的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．

6.【答案】C 
【解析】
【分析】
①用了解较少的学生数除以该组所占比例即可得到总人数；
②用学生总数乘以该组所占的比例得到基本了解的学生数；
③扇形所对圆心角的度数等于圆周角乘以该组所占比例；
④先求出不了解对应的百分比，再根据百分比之和等于1可得答案．
本题考查了两种统计图的认识，解题的关键是正确的利用这两种统计图的关系．
【解答】
解：①∵了解较少的学生有25人，占学生总数的50%，
∴参加问卷调查的学生有25÷50%=50人，故①正确；
②50×30%=15人，
∴参加问卷调查的学生中，“基本了解”的有15人，
故②错误；
③360°×30%=108°，
∴“基本了解”部分的扇形的圆心角的度数是108°，故③正确；
④∵不了解对应的百分比为550×100%=10%，
∴了解对应的百分比为1−(10%+50%+30%)=10%，故④正确；
故选：C．  
7.【答案】B 
【解析】
【分析】
本题考查了通过频数分布直方图获取信息解答问题的能力，解题关键是认真分析频数分布直方图，找出等待时间不少于6分钟的小组，读出人数再相加可得答案．
【解答】
解：由频数直方图可以看出：顾客等待时间不少于6分钟的人数即最后两组的人数为5+2=7人．
故选：B．  
8.【答案】D 
【解析】解：观察图象可知，抽查了50个学生，成绩在60.5～70.5范围的频数为2，成绩在70.5～80.5范围的频数比成绩在60.5～70.5范围的频数多1，成绩在70.5～80.5范围的频率为0.6，
故选项A，B，C正确，
故选：D．
利用直方图中的信息，一一判断即可．
本题考查频数分布直方图，解题的关键是读懂图象信息，灵活运用所学知识解决问题．

9.【答案】B 
【解析】解：分数在27分及以上的人数为8+10+6+2=26(人)，
所以这个班学生体育测试成绩是优秀的频数是26．
故选：B．
判断出分数在27分及以上的人数可得结论．
本题考查频数分布表，解题的关键是理解题意，灵活运用所学知识解决问题．

10.【答案】D 
【解析】略

11.【答案】A 
【解析】解：−π3、3−8、2、227、(−1)2021中，无理数有：：−π3、2，无理数出现的频数是2，
故选：A．
根据频数的定义解决问题即可．
本题考查频数与频率，有理数，无理数等知识，解题的关键是理解频数的定义，属于中考常考题型．

12.【答案】C 
【解析】解：A.由频数分布直方图可得：每天课外作业完成量不超过15个题的学生一共有(25+75+150+100)=350(名)，
350500×100%=70%，故每天课外作业完成量不超过15个题的该校学生按第一档布置作业，错误，不合题意；
B.∵每天课外作业完成量超过21个的学生有(25+15+15+5)=60(名)，
∴60500×100%=12%≠10%，故此选项错误，不合题意；
C.由A得，该校学生每天课外作业完成量的平均数不超过18，正确，符合题意；
D.∵500个数数据的中间是第250和251的平均数，
∴该校学生每天课外作业完成量的中位数在12−15之间，故此选项错误，不合题意；
故选：C．
利用频数分布直方图结合中位数的定义分别分析得出答案．
此题主要考查了频数分布直方图以及中位数的定义，正确利用条形统计图获取正确信息是解题关键．

13.【答案】24 
【解析】解：由统计表知这种报纸每份0.5元，
则买48份这种报纸应付48×0.5=24元，
故答案为：24．
由统计表得出每份0.5元，据此可求解．
本题主要考查统计表，解题的关键是根据统计表得出解题所需的数据．

14.【答案】15 
【解析】解：观察折线统计图可知：摸到红球的频率稳定在0.2，
设袋子中有x个黑球，
所以11+2+x=0.2，
解得x=2，
所以袋子中一共有5个球．
∴袋子中黑球的个数为2，
列表如下：

红
白
白
黑
黑
红

(白，红)
(白，红)
(黑，红)
(黑，红)
白
(红，白)

(白，白)
(黑，白)
(黑，白)
白
(红，白)
(白，白)

(黑，白)
(黑，白)
黑
(红，黑)
(白，黑)
(白，黑)

(黑，黑)
黑
(红，黑)
(白，黑)
(白，黑)
(黑，黑)

可能出现的结果有20种，并且它们出现的可能性相同．其中这两个球一红一白的结果有4种，
∴这两个球一红一白的概率为420=15，
故答案为：15．
根据摸到红球的频率，可以得到黑球的个数，进而可得袋子中一共有5个球；根据枚举法即可求摸出的两个球一红一白的概率．
此题主要考查了利用频率估计概率，本题利用了用大量试验得到的频率可以估计事件的概率．关键是根据红球的频率得到相应的等量关系．

15.【答案】12% 
【解析】解：第5组的频数=50−18−10−12−4=6，
∴第五组的频率=650=12%，
故答案为：12%．
根据频率的定义解决问题即可．
本题考查频数与频率，解题的关键是连接频率的定义，属于中考常考题型．

16.【答案】10 
【解析】
【分析】
本题考查的是组数的计算，属于基础题，只要根据组数的定义“数据分成的组的个数称为组数”来解即可．根据组数=(最大值−最小值)÷组距计算，注意小数部分要进位．
【解答】
解：在样本数据中最大值为143，最小值为50，它们的差是143−50=93，
已知组距为10，9310=9.3．
故可以分成10组．
故答案是10．  
17.【答案】解：(1)∵抽检的合格率为80%，
∴合格品有15×80%=12(个)，则残次品有3个，
而从编号①至编号⑭对应的产品中，只有编号②与编号⑭对应的产品为残次品，
故编号为⑮的产品不是合格品；

(2)按照优等品的标准，从小到大排列为：49.6，49.7，49.9，50.1，50.3，50.4，
中位数是：49.9+50.12=50(mm)；


(3)在优等品当中，编号②，⑩，⑧对应的产品尺寸不大于50.0mm，分别记为A1，A2，A3；编号④，⑥，⑪对应的产品尺寸大于50.0mm，分别记为B1，B2，B3，其中的特等品为A2，A3，B1，B2.根据题意列表：

B1
B2
B3
A1
(A1,B1)
(A1,B2)
(A1,B3)
A2
(A2,B1)
(A2,B2)
(A2,B3)
A3
(A3,B1)
(A3,B2)
(A3,B3)
由上表可知：共有9种等可能的结果，其中2件产品都是特等品的结果有4种，
所以抽取到的2件产品都是特等品的概率为49． 
【解析】(1)先求出残次品有3个，再由编号①与编号②对应的产品为残次品，即可得出结论；
(2)由中位数等于求解即可；
(3)画树状图，得出所有等可能的情况数，找出符合条件的情况数，然后根据概率公式求解即可．
此题考查的是用列表法或树状图法求概率、统计表以及中位数．用到的知识点为：概率=所求情况数与总情况数之比．

18.【答案】5  232  218  甲 
【解析】解：(1)将甲型种子抽样20穗质量进行分组统计，可得220 甲型种子抽样20穗质量出现次数最多的是232，共出现3次，因此众数为232，即m=232，
将乙型种子抽样20穗质量从小到大排列后，处在中间位置的两个数的平均数为217+2192=218，即中位数是218，也就是n=218，
故答案为：5，232，218；
(2)甲的中位数为215，乙的中位数为218，
所以此次调查中，单穗质量为217克的玉米在单穗质量排名(从高到低)中更靠前的是甲型玉米；
故答案为：甲；
(3)乙型玉米种子的产量表现更好，理由：乙型种子单穗质量的中位数大于甲型种子单穗质量的中位数，说明乙型种子大部分质量高于甲型种子(答案不唯一)．
(1)将甲型种子抽样20穗质量进行分组统计，进而得出a的值，利用中位数、众数的意义求出m、n的值；
(2)从中位数的角度得出结论；
(3)根据中位数的意义解答即可．
本题考查频数分布表，中位数、众数、方差的意义，理解中位数、众数、方差的意义，掌握中位数、众数、方差的计算方法是正确解答的前提．

19.【答案】解：(1)男生8≤x<9的频数为20−1−4−12=3，
补全的频数分布直方图如图：

(2)由a表格可知，m=9.2，n=(9.0+9.0)÷2=9.0，
∴m=9.2，n=9.0；
(3)根据题目中的信息可知，男生睡眠情况比较好，
理由为：睡眠时长的平均数相等，男生睡眠时长的众数、中位数高于女生．
故答案为：男生，睡眠时长的平均数相等，男生睡眠时长的众数、中位数高于女生． 
【解析】(1)求出男生8≤x<9的频数，然后即可将频数分布直方图补充完整；
(2)根据a表格的数据，可以得到m，n的值；
(3)根据c表格中的数据，可以得到睡眠情况比较好的，并写出相应的理由．
本题考查频数分布直方图、中位数、众数，解答本题的关键是明确题意，利用数形结合的思想解答．

20.【答案】50  144 
【解析】解：(1))∵非常满意的有18人，占36%，
∴此次调查中接受调查的人数：18÷36%=50(人)；
故答案为：50；

(2)此次调查中结果为满意的人数为：50−4−8−18=20(人)；


(3)扇形统计图中“满意”部分的圆心角为：360°×2050=144°；
故答案为：144°；

(4)画树状图得：

∵共有12种等可能的结果，选择回访市民为“一男一女”的有8种情况，
∴选择回访的市民为“一男一女”的概率为：812=23．
(1)由非常满意的有18人，占36%，即可求得此次调查中接受调查的人数；
(2)用总人数减去其他满意程度的人数，求出满意的人数，从而补全统计图；
(3)用360°乘以满意的人数所占的百分比即可得出答案；
(4)首先根据题意画出树状图，然后由树状图求得所有等可能的结果与选择回访市民为“一男一女”的情况，再利用概率公式即可求得答案．
此题考查了列表法或树状图法求概率以及条形与扇形统计图的知识．用到的知识点为：概率=所求情况数与总情况数之比．

21.【答案】14  0.2 
【解析】解：(1)m=40×35%=14，n=8÷40=0.2，
故答案为：14，0.2；
(2)补全频数分布直方图如下：

(3)∵成绩在94.5分以上的选手有4人，男生和女生各占一半，
∴2名是男生，2名是女生，
画树状图如下：

共有12种等可能的结果，其中确定的2名学生恰好是一名男生和一名女生的结果有8种，
∴确定的2名学生恰好是一名男生和一名女生的概率为812=23．
(1)由样本容量乘以频率得出m的值，再由频率的定义求出n的值即可；
(2)由(1)的结果，补全频数分布直方图即可；
(3)画树状图，共有12种等可能的结果，其中确定的2名学生恰好是一名男生和一名女生的结果有8种，再由概率公式求解即可．
此题考查了树状图法求概率、频数分布表和频数分布直方图等知识．正确画出树状图是解题的关键，用到的知识点为：概率=所求情况数与总情况数之比．

22.【答案】5  0.3 
【解析】解：(1)20÷0.4=50(人)，
a=50×0.1=5(人)，
b=15÷50=0.3，

故答案为：5，0.3；
(2)1000×(0.4+0.3)=700(人)，
答：该校1000学生中A等级和B等级防疫常识的学生大约有700人；
(3)1000×0.4=400(人)，1000×0.3=300(人)，
设将x名C、D等级的学生转化为A等级，
400+x≥2×300
解得：x≥200，
∴至少需要，200名C、D等级的学生转化为A等级的学生．
(1)根据频率=频数总数，可计算出得出总数，进而求出a、b的值，并补全频数分布直方图；
(2)根据样本中“非常了解”“比较了解”所占的百分比估计总体1000人中“非常了解”“比较了解”的人数；
(3)根据题意列不等式解答即可．
本题考查频数分布直方图、频数分布表以及用列表法求简单的随机事件发生的概率，理解频率=频数总数，列举出所有可能出现的结果情况是求概率的关键．

23.【答案】解：(1)本次抽查的学生有：6÷43.2°360∘=50(人)，
E组学生有：50−2−6−8−16−4=14(人)，
补全的频数分布直方图如图所示，

m=360°×1650=115.2°，
即m的值是115.2；

(2)本次测试的优秀率是：14+450=0.36；

(3)列表为：

男1
男2
女1
女2
男1
--
男2男1
女1男1
女2男1
男2
男1男2
--
女1男2
女2男2
女1
男1女1
男2女1
--
女2女1
女2
男1女2
男2女2
女1女2
--
由上表可知，从4名学生中任意选取2名学生共有12种等可能结果，其中恰好选到1名男生和1名女生的结果有8种，
所以选中的同学当中正好是一男一女的概率812=23． 
【解析】(1)根据B组的频数和所对的圆心角的度数，可以计算出本次调查的人数，再根据频数分布直方图中的数据，可以得到E组的频数，从而可以将频数分布直方图补充完整，根据直方图中的数据，可以计算出m的值；
(2)用优秀的人数除以总人数即可得出答案；
(3)根据题意列出图表，得出所有等可能的情况数，找出选中的同学当中恰好是一男一女的情况数，然后根据概率公式即可得出答案．
此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．也考查了扇形统计图、条形统计图的应用．