2020-2021学年1.2.3 充分条件、必要条件教学课件ppt

这是一份2020-2021学年1.2.3 充分条件、必要条件教学课件ppt，共25页。

教材新知知识点一 充分条件与必要条件提出问题在物理中，我们经常遇到这样的电路图：
问题1：图中A开关闭合时B灯一定亮吗？提示：一定亮．问题2：B灯亮时A开关一定闭合吗？提示：不一定，还可能是C开关闭合．
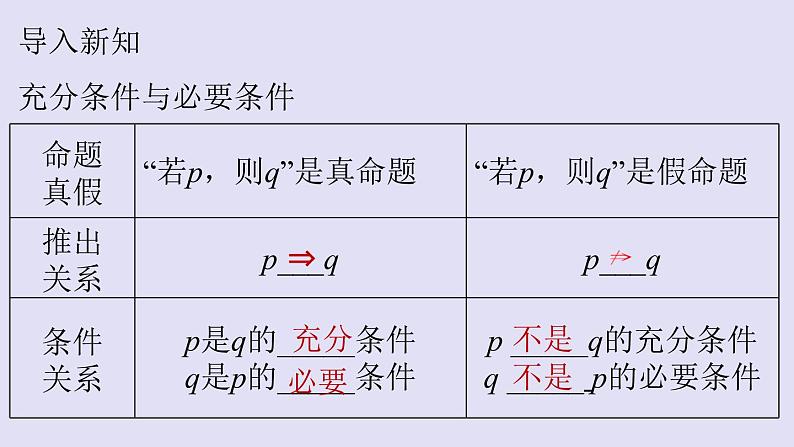
导入新知充分条件与必要条件
化解疑难1．p是q的充分条件是指“p成立可充分保证q成立，但是如果没有p，q也可能成立”．2．q是p的必要条件是指“要使p成立必须要有q成立”，或者说“若q不成立，则p一定不成立”；但即使有q成立，p未必会成立.
知识点二 充要条件如图是一物理电路图．问题1：图中开关A闭合，灯泡B亮；反之灯泡B亮，开关A一定闭合吗？
问题2：开关A闭合作为命题的条件p，灯泡B亮作为命题的结论q，你能判断p，q之间的推出关系吗？提示：p⇔q.
解：(1)在△ABC中，A∈(0，π)，B∈(0，π)，且A＋B＋C＝π.若cs2A＝cs2B，则A＝B；反之，若A＝B，则cs2A＝cs2B.因此，p是q的充要条件．(2)由x＞1可以推出x2＞1；由x2＞1，得x＜－1，或x＞1，不一定有x＞1.因此，p是q的充分不必要条件．(3)由(a－2)(a－3)＝0可以推出a＝2，或a＝3，不一定有a＝3；由a＝3可以得出(a－2)(a－3)＝0.因此，p是q的必要不充分条件．
类题通法充分、必要的判断方法判断p是q的什么条件，其实质是判断“若p，则q”及其逆命题“若q，则p”是真是假，原命题为真而逆命题为假，p是q的充分不必要条件；原命题为假而逆命题为真，则p是q的必要不充分条件；原命题为真，逆命题为真，则p是q的充要条件；原命题为假，逆命题为假，则p是q的既不充分也不必要条件，同时要注意反证法的运用．
活学活用指出下列各组命题中p是q的什么条件．(1)p：四边形的对角线相等，q：四边形是平行四边形；(2)p：(x－1)2＋(y－2)2＝0，q：(x－1)(y－2)＝0.
题型二 充分、必要条件的应用例2　已知p：－2≤x≤10，q：1－m≤x≤1＋m，且p是q的充分不必要条件，求实数m的取值范围．
类题通法应用充分条件和必要条件求参数的取值范围，主要是根据集合间的包含关系与充分条件和必要条件的关系，将问题转化为集合之间的关系，建立关于参数的不等式或不等式组求解，注意数形结合思想的应用．
活学活用已知P＝{x|a－4＜x＜a＋4}，Q＝{x|x2－4x＋3＜0}，若x∈P是x∈Q的必要条件，求实数a的取值范围．
随堂即时演练1．给定空间中的直线l及平面α，条件“直线l与平面α内无数条直线都垂直”是“直线l与平面α垂直”的 (　　)A．充分不必要条件　 B．必要不充分条件C．充要条件 D．既不充分也不必要条件
【解析】直线l与平面内无数直线都垂直，不能得到直线l⊥α，因为有可能是直线l在平面α内与一组平行直线垂直．若l⊥α，则直线l垂直于α内的所有直线．【答案】B
2．已知非零向量a，b，c，则“a·b＝a·c”是“b＝c”的 (　　)A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件
3.已知M＝{x|0＜x≤3}，N＝{x|0＜x≤2}，那么“a∈M”是“a∈N”的________条件．
4．在平面直角坐标系xOy中，直线x＋(m＋1)y＝2－m与直线mx＋2y＝－8互相垂直的充要条件是m＝________.
5．若p：x2＋x－6＝0是q：ax＋1＝0的必要不充分条件，求实数a的值．