





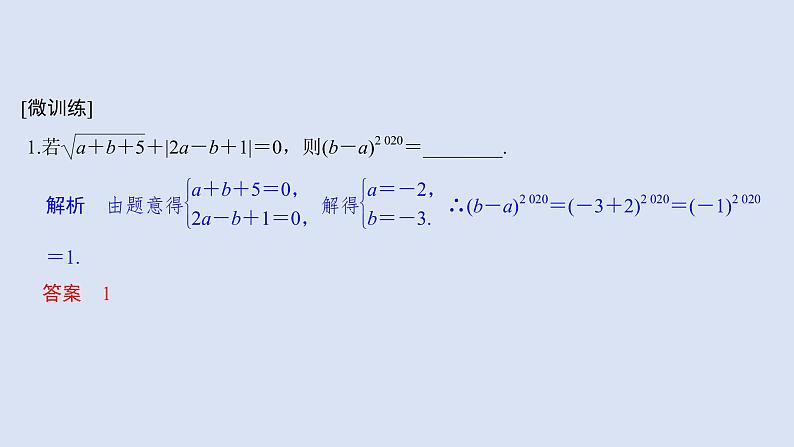

人教B版 (2019)必修 第一册2.1.3 方程组的解集教学课件ppt
展开法二 100-81=19(只),81÷3=27(元).假设剩余的19只鸡全是鸡翁,则5×19=95(元).因为95-73=22(元).所以鸡母:22÷(5-3)=11(只),鸡翁:19-11=8(只).
一般地,将多个方程联立,就能得到方程组.方程组中,由每个方程的解集得到的交集称为这个方程组的解集.
求方程组解集的依据还是等式的性质等,常用的方法是_________.
当方程组中未知数的个数大于方程的个数时,方程组的解集可能含有___________个元素.此时,如果将其中一些未知数看成_______,那么其他未知数往往能用这些未知数表示出来.
1.若ab=0,则a=0或b=0.( )2.二元方程的解集是无限集.( )提示 (x-1)2+(y-1)2=0的解集为{(x,y)|(1,1)}.3.二元一次方程组的解集可能是空集.( )
3.下列说法正确的是________(填序号).
①二元一次方程只有一个解;②二元一次方程组有无数个解;③二元一次方程组的解必是它所含的二元一次方程的解;④三元一次方程组一定由三个三元一次方程组成.解析 二元一次方程有无穷多个解,①不正确;二元一次方程组有一个解或无穷多个解或无解,②不正确;由方程组解集的定义知③正确;三元一次方程组中并非每一个方程均为三元一次方程,④不正确.答案 ③
1.常见的消元法有哪两种?提示 加减消元和代入消元.2.解二元二次方程组的基本思路是什么?提示 “消元”与“降次”.
解 (1)当1×2-a≠0即a≠2时,方程组有一个解.
解 法一 (代入法)由②,得y=4x-5 ③,把③代入①,得2x+3(4x-5)=-1,解这个一元一次方程,得x=1,把x=1代入③,得y=-1.所以这个方程组的解集为{(1,-1)}.法二 (加减法)①×2-②得y=-1,代入②得x=1,所以这个方程组的解集为{(1,-1)}.
角度3 二元一次方程组的实际应用【例1-3】 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质.若病人每餐需35单位蛋白质和40单位铁质,则每餐甲、乙两种原料各多少克恰好满足病人的需要?
解 设每餐甲、乙两种原料各需x g,y g,则有下表:
根据题意及上述表格,可列方程组
①-②,得y=30,把y=30代入②中,得x=28.答:每餐需甲种原料28 g,乙种原料30 g.
规律方法 (1)求二元一次方程组的解集常常利用消元的思想,消元的方法有代入消元法与加减消元法.(2)用二元一次方程组解决实际问题的步骤:①审题:弄清题意和题目中的数量关系.②设元:用字母表示题目中的未知数.③列方程组:根据两个等量关系列出方程组.④解方程组:利用代入消元或加减消元解出未知数的值.⑤检验并答:检验所求的解是否符合实际意义,然后作答.
【训练1】 随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需要600元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5 200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少元?
解 (1)设打折前甲品牌粽子每盒x元,乙品牌粽子每盒y元,
答:打折前甲品牌粽子每盒40元,乙品牌粽子每盒120元.(2)80×40+100×120-80×0.8×40-100×0.75×120=3 640(元).答:打折后购买这批粽子比不打折节省了3 640元.
①+②,得5x-z=14.①+③,得4x+3z=15.
把x=3,z=1代入③,得y=8.所以原方程组的解集为{(3,8,1)}.
规律方法 求三元一次方程组解集时,首先将系数较为简单的未知数消去,将“三元”转化为“二元”,再解二元一次方程组即可;或根据各未知数系数的特点,直接将方程相加(减)进行简便运算.
①-②×2,得5y-3z=8,④③-②,得3y-3z=6,⑤
把y=1,z=-1代入②,得x=2,所以原方程组的解集为{(2,1,-1)}.
题型三 求二元二次方程组的解集【例3】 求下列方程组的解集:
解 (1)把①代入②得x2+(x+1)2=13,整理得x2+x-6=0,解得x1=-3,x2=2.把x1=-3代入①,得y1=-2,把x2=2代入①,得y2=3,所以原方程组的解集为{(-3,-2),(2,3)}.
【训练3】 求下列方程组的解集:
即(x-2y+2)(x-2y-1)=0.∴x-2y+2=0或x-2y-1=0.
1.通过求方程组的解集提升数学运算素养.2.消元与降次是求方程组解集的基本方法.
1.某年级学生共有246人,其中男生人数y比女生人数x的2倍少2人,则下面所列的方程组中符合题意的是( )
2.三个二元一次方程2x+5y-6=0,3x-2y-9=0,y=kx-9有公共解的条件是k=( )
A.4 B.3 C.2 D.1
3.已知a-3b=2a+b-15=1,则代数式a2-4ab+b2+3的值为________.
2021学年2.1.3 方程组的解集教学课件ppt: 这是一份2021学年2.1.3 方程组的解集教学课件ppt,共24页。
高中数学人教B版 (2019)必修 第一册2.1.3 方程组的解集教学ppt课件: 这是一份高中数学人教B版 (2019)必修 第一册2.1.3 方程组的解集教学ppt课件,共13页。PPT课件主要包含了方程组的解集,消元法,x+3y+z34,x+2y+3z26等内容,欢迎下载使用。
高中人教B版 (2019)2.2.2 不等式的解集教学课件ppt: 这是一份高中人教B版 (2019)2.2.2 不等式的解集教学课件ppt,共36页。PPT课件主要包含了新知探究,1不等式的解集,2不等式组的解集,所有解,绝对值不等式,-mm,a-b,拓展深化微判断,微训练,答案等内容,欢迎下载使用。













