






2020-2021学年1.2.1 命题与量词教学ppt课件
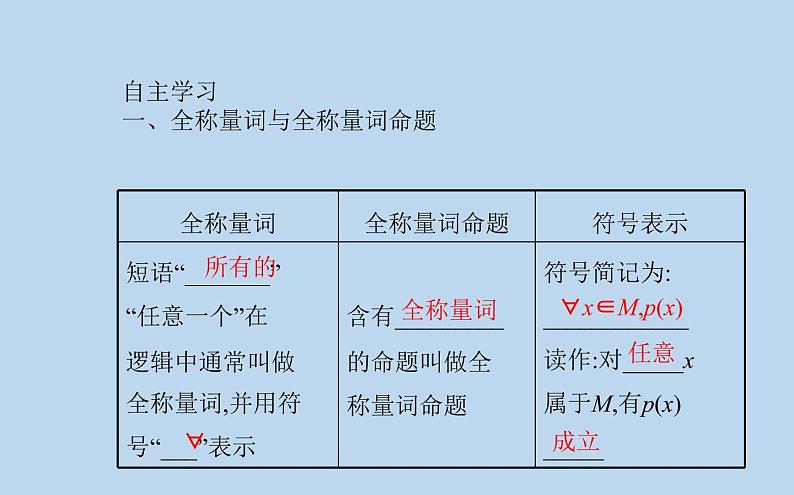
展开自主学习一、全称量词与全称量词命题
思考:全称量词命题中的“x,M与p(x)”表达的含义分别是什么?提示:元素x可以表示实数、方程、函数、不等式,也可以表示几何图形,相应的集合M是这些元素的某一特定的范围.p(x)表示集合M的所有元素满足的性质.如“任意一个自然数都不小于0”,可以表示为“∀x∈N,x≥0”.
二、存在量词与存在量词命题
∃x0∈M,p(x0),
判断:(正确的打“√”,错误的打“×”)(1)“有些”“某个”“有的”等短语不是存在量词.( )(2)全称量词的含义是“任意性”,存在量词的含义是“存在性”.( )(3)全称量词命题一定含有全称量词,存在量词命题一定含有存在量词.( )
提示:(1)“有些”“某个”“有的”等短语是存在量词,故说法是错误的.(2)结合全称量词和存在量词的含义知,这种说法是正确的.(3)有些命题虽然没有写出全称量词和存在量词,但其意义具备“任意性”或“存在性”,这类命题也是全称量词命题或存在量词命题,如“正数大于0”即“所有正数都大于0”,故说法是错误的.答案:(1)× (2)√ (3)×
【知识点拨】1.全称量词命题及其真假的判断方法(1)全称量词命题就是陈述某集合中所有元素都具有某种性质的命题,常见的全称量词还有“一切”“每一个”等,相应的词语是“都”.
(2)有些命题省去了全称量词,但仍是全称量词命题,如“有理数是实数”,就是“所有的有理数都是实数”.(3)要判断全称量词命题“∀x∈M,p(x)”为假命题,只需要在集合M中找到一个元素x0,使得p(x0)不成立即可;要判断全称量词命题为真命题,必须对集合M中的每一个元素x,证明p(x)成立.简单地说,判断全称量词命题真假的步骤为“先找反例后证明”.
2.存在量词命题及其真假的判断方法(1)存在量词命题就是陈述某集合中存在一个或部分元素具有某种性质的命题,常见的存在量词还有“有的”“存在”等.(2)要判断存在量词命题“∃x0∈M,p(x0)”为真命题,只需要在集合M中找到一个元素x0,使得p(x0)成立即可;要判断存在量词命题为假命题,必须说明集合M中不存在元素x0,使得p(x0)成立.简单地说,判断存在量词命题真假的步骤为“先找正例后证明”.
类型 一 全称量词命题的构成与真假判断 【典型例题】1.下列是全称量词命题且是真命题的是( )A.∀x∈R,x2>0 B.∀x∈Q,x2∈QC.∃x0∈Z,x02>1 D.∀x,y∈R,x2+y2>0
2.用全称量词把下列语句写成全称量词命题,并判断真假:(1)x2+2x+3≥2.(2)负数都没有对数.(3)终边相同的角的正弦值相等.【解题探究】1.全称量词命题的形式是什么?2.判断全称量词命题真假的方法是什么?
探究提示:1.全称量词命题的一般形式为“∀x∈M,p(x)”.2.若某一集合存在不满足某一性质的反例,则全称量词命题是假命题,不存在反例,就是真命题.【解析】1.选B.由于x=0时,x2=0,故A假;任意有理数的平方都是有理数,故B真;选项C为特称命题;由于,当x=y=0时,x2+y2=0,故D假.综上所述,选B.2.(1)∀x∈R,x2+2x+3≥2.x2+2x+3=(x+1)2+2≥2.真命题.(2)所有的负数都没有对数.真命题.(3)所有终边相同的角的正弦值相等.真命题.
【拓展提升】全称量词命题的形式定义与真假判断(1)全称量词命题的统一形式为“∀x∈M,p(x)”,∀表示“任意”“所有”等量词,集合M表示给定的范围,p(x)表示某一性质.(2)判断全称量词命题的真假,可以先找反例,若找到一个反例,说明全称量词命题是假命题,若找不到反例,就可以尝试证明命题是真命题.
【变式训练】1.“∀x∈Z,2x+1都是奇数”是 命题(填真、假).2.用全称量词把下列语句写成全称量词命题,并判断真假:(1)sin2x=2sinxcsx.(2)三角形有外接圆.(3)非负实数有两个偶次方根.
【解析】1.“∀x∈Z,2x+1都是奇数”是真命题.答案:真2.(1)∀x∈R,sin2x=2sinxcsx.真命题.(2)任意三角形都有外接圆.真命题.(3)所有的非负实数都有两个偶次方根.假命题.
类型 二 存在量词命题的构成与真假判断 【典型例题】1.存在量词命题“∃x0∈R, x02
【变式训练】1.“∃x0∈N,x0是奇数且是合数”是 命题(填真、假).2.用存在量词将下列语句写成存在量词命题,并判断真假:(1)奇函数也可以是偶函数.(2)不是每一个四边形都有外接圆.
【解析】1.“∃x0∈N,x0是奇数且是合数”是真命题.答案:真2.(1)存在函数既是奇函数又是偶函数,如f(x)=0,x∈R,真命题.(2)有的四边形没有外接圆.真命题.
类型 三 含有一个量词的命题及其综合应用 【典型例题】1.若“∃x0∈R,x02+2x0+2=m”是真命题,则实数m的取值范围是 .2.已知命题p:“∃x0∈R,sinx0
【解题探究】1.一元二次方程有实根的条件是什么?是否可以利用函数y=x2+2x+2的图象解答?2.题2中p,q的真假如何?探究提示:1.利用关于x的一元二次方程有实根的充要条件(判别式Δ≥0)解决.也可以采用数形结合的思想将题目转化为y=x2+2x+2的图象与直线y=m有公共点.2.命题p,q都是真命题.
【解析】1.方法一:由于“∃x0∈R,x02+2x0+2=m”是真命题,则实数m的取值集合就是二次函数f(x)=x2+2x+2的值域,即{m|m≥1}.方法二:依题意,方程x2+2x+2-m=0有实数解,∴Δ=4-4(2-m)≥0,解得m≥1.答案:[1,+∞)
2.由于p∧q是真命题,则p,q都是真命题.因为“∃x0∈R,sinx0
【拓展提升】能成立与恒成立问题的解法(1)若含有参数的方程能成立,求参数的取值范围一般转化为求函数的值域.(2)若含有参数的不等式f(x)≤m在区间D上能成立,则f(x)min≤m;若不等式f(x)≥m在区间D上能成立,则f(x)max≥m.
(3)若含有参数的不等式f(x)≤m在区间D上恒成立,则f(x)max≤m;若含有参数的不等式f(x)≥m在区间D上恒成立,则f(x)min≥m.(4)存在量词命题是真命题,可以转化为能成立问题,全称量词命题是真命题,可以转化为恒成立问题解决.
【易错误区】应用函数与方程思想时忽视变量的取值范围致误【典例】若∃x0∈R,使cs2x0+2sinx0+a=0,则实数a的取值范围是 .
【解析】依题意,若∃x0∈R,使cs2x0+2sinx0+a=0,则得a=-cs2x0-2sinx0=2sin2x0-2sinx0-1=2(sinx0- )2- ,令t=sinx0,则a=2(t- )2- ,-1≤t≤1①. 由于函数a(t)在-1≤t≤ 上单调递减,在
学业测试1.下列全称量词命题是真命题的是( )A.实数都有倒数 B.自然数都是正整数C.小数都是有理数 D.无理数都是无限不循环小数【解析】选D.由于0没有倒数,故A错误;由于0不是正整数,故B错误;由于无限不循环小数是无理数,故C错误,D正确.
2.下列命题是全称量词命题的个数是( )①任何实数都有平方根;②所有的素数都是奇数;③有的等差数列也是等比数列;④三角形的内角和是180°.A.0 B.1 C.2 D.3【解析】选D.命题①②含有全称量词,而命题④可以叙述为“每一个三角形的内角和都是180°”,故有三个全称量词命题.
3.下列存在量词命题是假命题的是( )A.∃x0∈R,sinx0=csx0B.∃x0∈R,sinx0>csx0C.∃x0∈R,sinx0+csx0=2D.∃x0∈R,sinx0+csx0=sinx0csx0
【解析】选C.当x0= 时,sinx0=csx0,A正确;当x0= 时,sinx0>csx0,B正确;由于sinx0+csx0= sin(x0+ )≤ ,故C错误;令t=sinx0+csx0= sin(x0+ ),则- ≤t≤ ,sinx0+csx0=sinx0csx0,即t= ,得t2-2t-1=0,解得t=1- ,或t=1+ (舍去).D正确.
4.存在量词命题“有些向量的坐标等于其终点的坐标”是 命题(填“真”或“假”).【解析】当向量的起点在坐标原点时,向量的坐标等于其终点的坐标.答案:真
5.对任意x>3,x>a恒成立,则实数a的取值范围是 .【解析】对任意x>3,x>a恒成立,即大于3的数恒大于a,∴a≤3.答案:(-∞,3]
6.若存在x0∈R,使ax02+2x0+a<0成立,求实数a的取值范围.【解析】当a≤0时,显然存在x0∈R,使ax02+2x0+a<0;当a>0时,必须Δ=4-4a2>0,解得-1
人教B版 (2019)必修 第一册1.2.1 命题与量词教课内容课件ppt: 这是一份人教B版 (2019)必修 第一册1.2.1 命题与量词教课内容课件ppt,共28页。PPT课件主要包含了真假判断,每一个,至少有一个,∀x∈Mrx,∃x∈Msx等内容,欢迎下载使用。
人教B版 (2019)必修 第一册3.3 函数的应用(一)教学课件ppt: 这是一份人教B版 (2019)必修 第一册3.3 函数的应用(一)教学课件ppt,共23页。PPT课件主要包含了题型探究,课堂小结等内容,欢迎下载使用。
人教B版 (2019)必修 第一册1.1.1 集合及其表示方法教学课件ppt: 这是一份人教B版 (2019)必修 第一册1.1.1 集合及其表示方法教学课件ppt,共20页。PPT课件主要包含了课堂探究,集合中的元素是确定的,集合中的元素是互异的,正整数集,自然数集,整数集,有理数集,实数集,课堂训练,课堂小结等内容,欢迎下载使用。













