






2021学年2.2.3 一元二次不等式的解法教学课件ppt
展开1.某杂志以每本2元的价格发行时,发行量为10万册.经过调查,若价格每提高0.2元,发行量就减少5 000册.要使杂志社的销售收入大于22.4万元,每本杂志的价格应定在怎样的范围内?
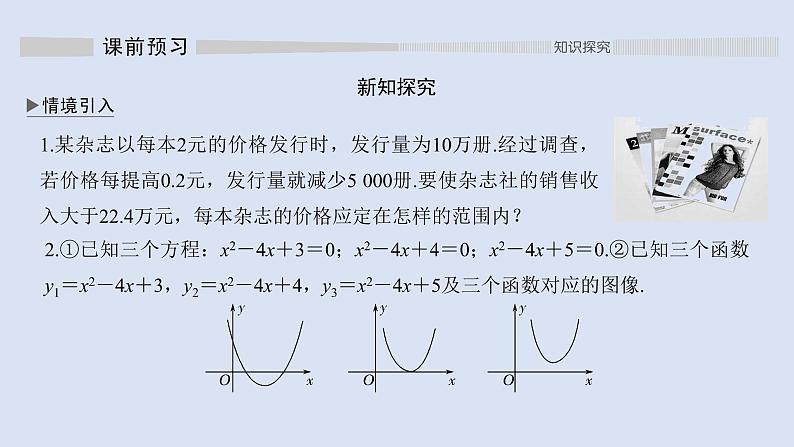
2.①已知三个方程:x2-4x+3=0;x2-4x+4=0;x2-4x+5=0.②已知三个函数y1=x2-4x+3,y2=x2-4x+4,y3=x2-4x+5及三个函数对应的图像.
问题 1.观察实例1中的不等式,指出其含未知数个数及未知数的次数?2.观察实例2,①中三个方程的解分别为x1=1,x2=3;x1=x2=2;无解,②中三个函数与x轴交点横坐标分别为1,3;2;无交点.由图像观察可知在②中三个函数中,x分别取何值函数值为正、负?提示 设每本杂志价格提高x元,则发行量减少2.5x万册,杂志社的销售收入为(2+x)(10-2.5x)万元.根据题意,得(2+x)(10-2.5x)>22.4,即5x2-10x+4.8<0,解此不等式,最终得每本杂志的价格范围.1.只含一个未知数,并且未知数的最高次数是2.2.对于y1=x2-4x+3,当x<1或x>3时,y1=x2-4x+3>0,当1
1.一元二次不等式的概念
一般地,形如ax2+bx+c>0的不等式称为一元二次不等式,其中a,b,c是常数,而且a_____0.一元二次不等式中的不等号也可以是“<”“≥”“≤”等.
2.求一元二次不等式的解集的方法
(1)因式分解法一般地,如果x1<x2,则不等式(x-x1)(x-x2)<0的解集是_____________,不等式(x-x1)(x-x2)>0的解集是_______________________.(2)配方法一元二次不等式ax2+bx+c>0(a≠0)通过配方总是可以变为(x-h)2>k或(x-h)2<k的形式,然后根据k的正负等知识,就可以得到原不等式的解集.
(-∞,x1)∪(x2,+∞)
1.不等式ax2+x-1<0是一元二次不等式.( )提示 只有当a≠0时,ax2+x-1<0才是一元二次不等式.2.不等式x2-5y<0是一元二次不等式.( )提示 x2-5y<0含有两个未知数,故不是一元二次不等式.3.不等式x2-2x+3>0的解集为R.( )
1.不等式(x+2)(x-3)>0的解集是________.
答案 {x|x>3或x<-2}
2.不等式x2<2的解集是________.
1.a2b+2ab2+9>0(ab≠0)可看作一元二次不等式吗?
提示 可以,把b看作常数,则是关于a的一元二次不等式;把a看作常数,则是关于b的一元二次不等式.
2.举例说明某些一元二次不等式的解集为.
提示 例如x2+x+1≤0的解集为.
题型一 解不含参数的一元二次不等式角度1 因式分解法【例1-1】 求下列一元二次不等式的解集.
(1)x2-10x-600>0;(2)-3x2+2x+1≥0.解 (1)因为x2-10x-600=(x+20)(x-30),所以原不等式等价于(x+20)(x-30)>0,因此所求解集为(-∞,-20)∪(30,+∞).
(2)原不等式可化为3x2-2x-1≤0 ①,
角度2 配方法【例1-2】 求下列不等式的解集.
(1)4(2x2-2x+1)>x(4-x);(2)-3x2+6x≤2.解 (1)由原不等式得8x2-8x+4>4x-x2.∴原不等式可化为9x2-12x+4>0. ①
(2)原不等式可化为3x2-6x+2≥0 ①,而3x2-6x+2=3(x-1)2-1,
规律方法 解一元二次不等式的一般步骤第一步:分解为两个因式的乘积的形式或配方成完全平方式形式;第二步:写出不等式的解集.
【训练1】 求下列不等式的解集:
(1)4x2-4x+1>0;(2)-x2+6x-10>0.解 (1)∵4x2-4x+1=(2x-1)2,∴原不等式可化为(2x-1)2>0,
(2)∵原不等式化可为x2-6x+10<0,x2-6x+10=(x-3)2+1,∴原不等式等价于(x-3)2+1<0,∴原不等式的解集为.
题型二 解含参数的一元二次不等式【例2】 解关于x的不等式(a∈R):
(1)2x2+ax+2>0;(2)x2-(a+a2)x+a3>0.解 (1)Δ=a2-16,下面分情况讨论:①当Δ<0,即-4
此时原不等式等价于(x-x1)(x-x2)>0,∴x
当a>1时,有a
规律方法 解含参数的一元二次不等式的步骤
特别提醒 对应方程的根优先考虑用因式分解确定,分解不开时再求判别式Δ,用求根公式计算.
【训练2】 解关于x的不等式x2+2x+1-a2≤0(a∈R).
解 原不等式等价于(x+1+a)(x+1-a)≤0.(1)当-1-a<-1+a,即a>0时,-1-a≤x≤-1+a;(2)当-1-a=-1+a,即a=0时,不等式即为(x+1)2≤0,∴x=-1;(3)当-1-a>-1+a,即a<0时,-1+a≤x≤-1-a.综上,当a>0时,原不等式的解集为{x|-1-a≤x≤-1+a};当a=0时,原不等式的解集为{x|x=-1};当a<0时,原不等式的解集为{x|-1+a≤x≤-1-a}.
题型三 简单的高次不等式与分式不等式【例3】 求下列不等式的解集:
解 (1)不等式(x+3)(x2-4)≤0可化为(x+3)(x+2)(x-2)≤0,令(x+3)(x+2)(x-2)=0,得x=-3或x=-2或x=2.
利用数轴,可得不等式的解集为(-∞,-3]∪[-2,2].
(2)由题意知x+5≠0,因此(x+5)2>0,原不等式两边同时乘以(x+5)2可得5(x+5)≤(x+5)2且x+5≠0,即x(x+5)≥0且x≠-5,因此所求不等式的解集为(-∞,-5)∪[0,+∞).
【训练3】 求下列不等式的解集.
(2)由题意知x+2≠0,因此(x+2)2>0,原不等式两边同时乘以(x+2)2可得(1-x)(x+2)≥2(x+2)2且x+2≠0,即3(x+2)·(x+1)≤0且x≠-2,因此原不等式的解集为(-2,-1].
题型四 三个“二次”间的关系及应用【例4】 已知二次函数y=ax2+(b-8)x-a-ab,且y>0的解集为(-3,2).
(1)求二次函数的解析式;(2)当关于x的不等式ax2+bx+c≤0的解集为R时,求c的取值范围.解 (1)因为y>0的解集为(-3,2),所以-3,2是方程ax2+(b-8)x-a-ab=0的两根,
所以y=-3x2-3x+18.
规律方法 三个“二次”之间的关系(1)三个“二次”中,二次函数是主体,讨论二次函数主要是将问题转化为一元二次方程和一元二次不等式的形式来研究.(2)讨论一元二次方程和一元二次不等式又要将其与相应的二次函数相联系,通过二次函数的图像及性质来解决问题,关系如下:
特别提醒 由于忽视二次项系数的符号和不等号的方向易写错不等式的解集形式.
(1)求a,c的值;(2)解关于x的不等式ax2+(ac+2)x+2c≥0.
1.(1)通过从实际情景中抽象出一元二次不等式的过程提升数学抽象素养.(2)通过解一元二次不等式培养数学运算素养.2.配方法是解一元二次不等式的基本方法,而因式分解法较为简单.
2.设集合A={x|(x-1)2<3x+7,x∈R},则集合A∩Z中有________个元素.
解析 由(x-1)2<3x+7,解得-1<x<6,即A={x|-1<x<6},则A∩Z={0,1,2,3,4,5}.故A∩Z共有6个元素.答案 6
3.已知x=1在不等式k2x2-6kx+8≥0的解集内,则k的取值范围是______________.
解析 x=1在不等式k2x2-6kx+8≥0的解集内,把x=1代入不等式得k2-6k+8≥0,解得k≥4或k≤2.答案 {k|k≥4或k≤2}
4.解不等式x2-3|x|+2≤0.
解 x2-3|x|+2≤0⇔|x|2-3|x|+2≤0⇔(|x|-1)·(|x|-2)≤0⇔1≤|x|≤2.当x≥0时,1≤x≤2;当x<0时,-2≤x≤-1.∴原不等式的解集为{x|-2≤x≤-1或1≤x≤2}.
人教B版 (2019)必修 第一册2.2.3 一元二次不等式的解法教学ppt课件: 这是一份人教B版 (2019)必修 第一册2.2.3 一元二次不等式的解法教学ppt课件,共40页。
高中数学2.2.3 一元二次不等式的解法教学课件ppt: 这是一份高中数学2.2.3 一元二次不等式的解法教学课件ppt,共40页。
高中数学人教B版 (2019)必修 第一册1.2.1 命题与量词教学ppt课件: 这是一份高中数学人教B版 (2019)必修 第一册1.2.1 命题与量词教学ppt课件,共28页。PPT课件主要包含了新知探究,全称量词,存在量词,拓展深化微判断,微训练,微思考,素养落地,素养训练,答案C,答案B等内容,欢迎下载使用。













