高中人教B版 (2019)1.1.1 集合及其表示方法教学ppt课件

这是一份高中人教B版 (2019)1.1.1 集合及其表示方法教学ppt课件，共31页。PPT课件主要包含了新知探究，确定的，不同的，确定性，互异性，无序性，有限个，无限个，a∈A，a∉A等内容，欢迎下载使用。

问题2：渔民网中的鱼组成的集合和湖中的鱼组成的集合有怎样的关系？问题3：如果有两个渔民都在打渔，他们各自渔网中的鱼的种类组成两个集合，那么求这两个集合中的相同鱼的种类组成的新集合是集合的什么运算？将两个渔网中的鱼组成的集合中的鱼的种类合在一起的过程又是集合的哪种运算？
链接：数学家所说的集合是指渔网中的鱼，很显然渔网中的对象都是确定的、无序的和互异的；渔网中的鱼组成的集合是湖中的鱼组成集合的一部分，是湖中鱼构成集合的一个子集；两个渔网中相同鱼的种类组成的集合是两个集合的交集，两渔网鱼的种类合在一起就构成了两个集合的并集.
中华人民共和国成立70周年阅兵式于2019年10月1日10：00在北京天安门广场隆重举行，阅兵编59个方(梯)队，参与人数约1.5万人，是历年来规模最大的一次.
问题　参加阅兵式的所有女兵能否组成一个集合？提示　参加阅兵式的所有女兵能够组成一个集合.
(1)元素与集合的概念①把一些能够_________、_________对象汇集在一起，就说由这些对象组成一个集合(有时简称为集)，组成集合的每个对象都是这个集合的元素.集合通常用英文大写字母A，B，C，…表示，集合的元素通常用英文小写字母a，b，c，…表示.一般地，我们把不含任何元素的集合称为空集，记作.
②集合的元素特点_________：集合的元素必须是确定的._________：对于一个给定的集合，集合中的元素一定是不同的._________：集合中的元素可以任意排列，与次序无关.③集合相等：给定两个集合A和B，如果组成它们的_______完全相同，就称这两个集合相等，记作A＝B.④集合的分类根据集合含有的元素个数分为两类：有限集：含有_________元素的集合(空集可以看成包含0个元素的集合，所以空集是有限集).无限集：含有_________元素的集合.
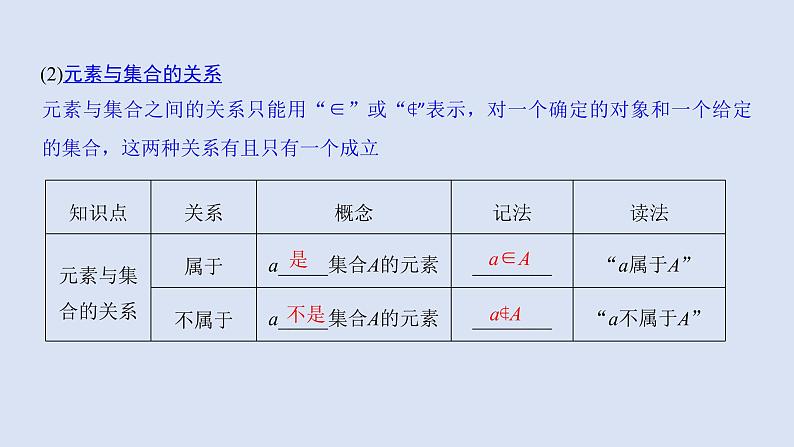
(2)元素与集合的关系
元素与集合之间的关系只能用“∈”或“∉”表示，对一个确定的对象和一个给定的集合，这两种关系有且只有一个成立
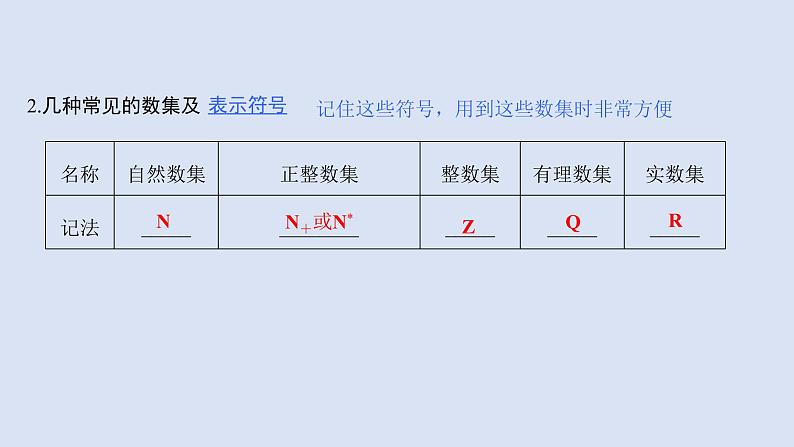
记住这些符号，用到这些数集时非常方便
1.漂亮的花可以组成集合.( )提示　“漂亮的花”具有不确定性，故不能组成集合.2.由方程x2－4＝0和x－2＝0的根组成的集合中有3个元素.( )提示　由于集合中的元素具有互异性，故由两方程的根组成的集合中有2个元素.3.元素1，2，3和元素3，2，1组成的集合是不相等的.( )提示　集合中的元素具有无序性，所以元素1，2，3和元素3，2，1组成的集合是同一集合.
给出下列说法：①在一个集合中可以找到两个相同的元素；②好听的歌能组成一个集合；③高一(1)班所有姓氏构成的集合；④把1，2，3三个数排列，共有6种情况，因此由这三个数组成集合有6个.其中正确的个数为(　　)A.0 B.1 C.2 D.3
解析　①错误，集合中的元素是互不相同的；②错误，好听的歌是不确定的，所以好听的歌不能组成一个集合.③正确，高一(1)班的姓氏是确定的，所以能构成集合.④错误，因为集合中的元素满足无序性，故由1，2，3三个元素只能组成一个集合.答案　B
1.我班所有的“追梦人”能否构成一个集合？提示　不能构成集合，因为“追梦人”没有明确的标准.2.设集合A表示“1～10以内的所有素数”，3，4这两个元素与集合A有什么关系？如何用数学语言表示？提示　3是集合A中的元素，即3属于集合A，记作3∈A；4不是素数，即4不属于集合A，记作4∉A.
题型一　集合概念的理解【例1】　考察下列每组对象能否构成一个集合：
解　(1)对任意一个实数能判断出是不是“不超过20的非负数”，所以能构成集合；(2)方程的两个解是x＝±3能构成集合；(3)“矮个子”无明确的标准，对于某个人算不算矮个子无法客观地判断，因此不能构成一个集合；
规律方法　判断一组对象能否构成集合的关键在于看是否有明确的判断标准，使给定的对象是“确定无疑”的还是“模棱两可”的.如果是“确定无疑”的，就可以构成集合；如果是“模棱两可”的，就不能构成集合.
【训练1】　(1)下列给出的对象中能构成集合的是(　　)
A.著名物理家 B.很大的数C.聪明的人 D.小于3的实数(2)下列各组对象可以构成集合的是(　　)A.数学必修第一册课本中所有的难题B.小于8的所有素数C.直角坐标平面内第一象限的一些点D.所有小的正数
解析　(1)只有选项D有明确的标准，能构成一个集合.(2)A中“难题”的标准不确定，不能构成集合；B能构成集合；C中“一些点”无明确的标准，对于某个点是否在“一些点”中无法确定，因此“直角坐标平面内第一象限的一些点”不能构成集合；D中没有明确的标准，所以不能构成集合.答案　(1)D　(2)B
(2)①正确；②③④不正确.答案　(1)ACD　(2)A
规律方法　判断元素和集合关系的两种方法(1)直接法：集合中的元素是直接给出的.(2)推理法：对于某些不便直接表示的集合，只要判断该元素是否满足集合中元素所具有的特征即可.
【训练2】　(1)给出下列说法：
解析　(1)实数集中没有最小的元素，故①不正确；对于②，若a∈Z，则－a也是整数，故－a∈Z，所以②也不正确；只有③正确.
答案　(1)B　(2)B
题型三　元素特性的应用【例3】　已知集合A是由a－2，2a2＋5a，12三个元素组成的，且－3∈A，求实数a.
解　由－3∈A，可得－3＝a－2或－3＝2a2＋5a，
当a＝－1时，a－2＝－3，2a2＋5a＝－3，不符合集合中元素的互异性，故a＝－1应舍去.
规律方法　利用集合中元素的互异性求参数的策略及注意点(1)策略：根据集合中元素的确定性，可以解出字母的所有可能值，再根据集合中的元素的互异性对求得参数值进行检验.(2)注意点：利用集合中元素的互异性解题时，要注意分类讨论思想的应用.
【训练3】　已知集合A含有两个元素a－3和2a－1，若－3是集合A中的元素，试求实数a的值.
解　因为－3是集合A中的元素，所以－3＝a－3或－3＝2a－1.若－3＝a－3，则a＝0，此时集合A含有两个元素－3，－1，符合要求；若－3＝2a－1，则a＝－1，此时集合A含有两个元素－4，－3，符合要求.综上所述，满足题意的实数a的值为0或－1.
一、素养落地1.通过集合概念及元素与集合关系的学习，重点培养数学抽象素养及提升数学运算素养.2.研究对象能否构成集合，就是要看是否有一个确定的标准，能确定一个个体是否属于这个总体，如果有，能构成集合，如果没有，就不能构成集合.这是判断能否构成集合的依据.
二、素养训练1.考察下列每组对象，能构成集合的是(　　)
①中国各地的美丽乡村；②直角坐标系中横、纵坐标相等的点；③不小于3的自然数；④截止到2020年1月1日，参加“一带一路”的国家.A.③④ B.②③④ C.②③ D.②④解析　①中“美丽”标准不明确，不符合确定性，②③④中的元素标准明确，均可构成集合，故选B.答案　B
2.已知1，x，x2三个实数构成一个集合，则x满足的条件是(　　)
A.x≠0 B.x≠1C.x≠±1 D.x≠0且x≠±1
3.已知集合A中的元素x满足x≥2，若a∉A，则实数a的取值范围是________.
解析　由题意a不满足不等式x≥2，即a<2.答案　a<2