小学数学北师大版五年级上册5 找质数学案及答案

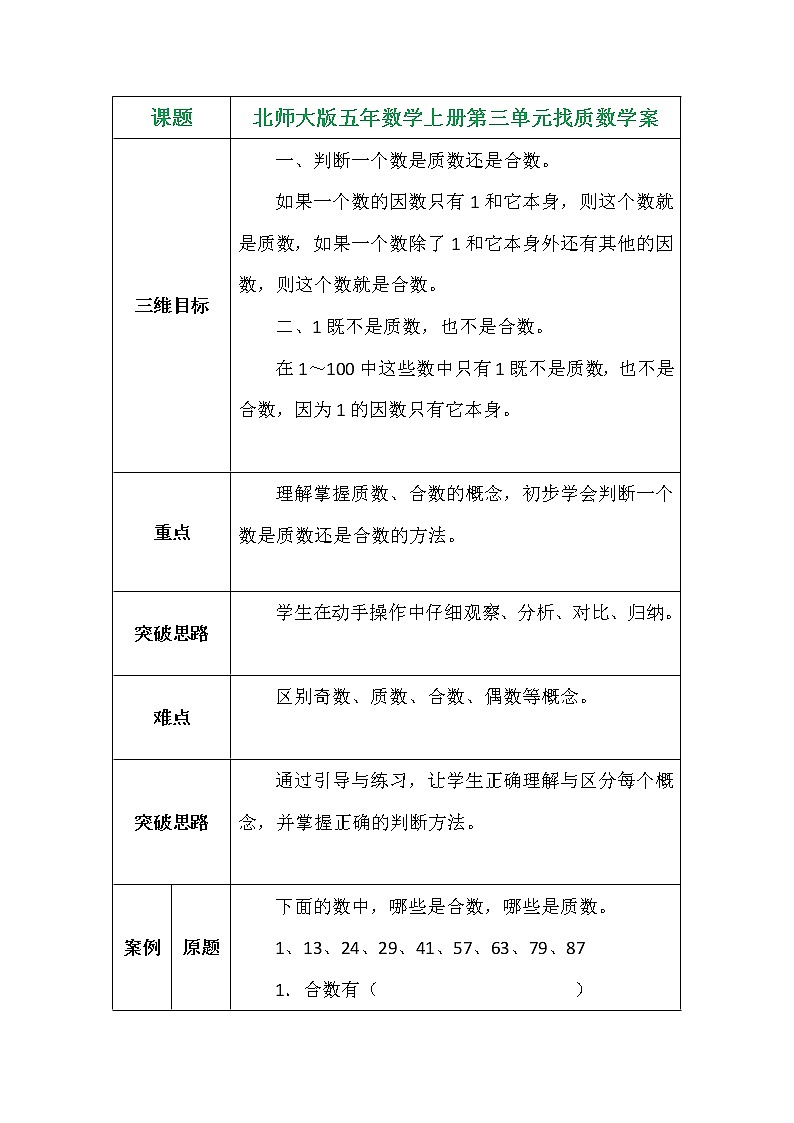
课题

北师大版五年数学上册第三单元找质数学案

三维目标

一、判断一个数是质数还是合数。

如果一个数的因数只有1和它本身，则这个数就是质数，如果一个数除了1和它本身外还有其他的因数，则这个数就是合数。

二、1既不是质数，也不是合数。

在1～100中这些数中只有1既不是质数，也不是合数，因为1的因数只有它本身。

重点

理解掌握质数、合数的概念，初步学会判断一个数是质数还是合数的方法。

突破思路

学生在动手操作中仔细观察、分析、对比、归纳。

难点

区别奇数、质数、合数、偶数等概念。

突破思路

通过引导与练习，让学生正确理解与区分每个概念，并掌握正确的判断方法。

案例

原题

下面的数中，哪些是合数，哪些是质数。

1、13、24、29、41、57、63、79、87

1．合数有（                     ）

2．质数（                     ）

解析

解答：1.24、57、63、87

2.13、29、41、79

点拔

有的学生做题时，可能会漏写或判断错误而导致出错。这都是因为没有掌握质数与合数的概念及做题时的粗心造成的。

归纳

学生在解题没有理解和掌握好质数和合数的概念，质数和合数的判断要从这个数的因数中是否除1和本身外还有其他的因数，如果有其他的因数就是合数，如果没有就是质数。但有一个特别的数也要记住，那就是1既不是质数，也不是合数。

课后答案

【教材第40页“练一练”】

1.1 2质24 合24合35合

2．质数：23、29、11

合数：27、9、33、14、25、99

3.（略）

4.（略）

作  业

解决问题。

1．一个长方形的长和宽都是质数，并且周长是36厘米，这个长方形的面积最大可以是多少平方厘米？

2.1430名学生参加团体操，分成人数相等的若干队，每队人数在100至200之间，问哪几种分法？

存在问

题摘要

（1）.                                ；

（2）.                                ；

（3）.                                。

反思

本节课的教学是先让学生在游戏中拼长方形，让学生在快乐的氛围中学习，从而激发学生的探究欲望。学生拼长方形的过程也是探究因数的过程，通过游戏，学生能更加形象、直观地把2～12的因数找出来。再引导学生通过仔细观察发现表格中的因数特征，从而引出质数和合数，最后让学生自学教材，了解质数和合数的概念。这样的学习方式，以学生自主探究为主体，教师适时地引导，极大的调动了学生的学习积极性，同时培养了学生的仔细观察的能力。整课的教学都是以学生的自主学习为主，以学生已有的生活经历和知识为基础，让学生通过动手操作、小组交流、合作讨论、归纳总结学习数学，提高学生学习数学的能力。

课外资料

1为什么不是质数？

我们在学习质数、合数的概念时，会疑熟：1为什么既不是质数也不是合数。

有人要问，“1”也只能被1和它本身整除，为什么不能算质数呢？而且“1”算作质数后，就不用再追加这么一句，岂不是更简单吗？

这要从分解质因数谈起。比如，1001 能被哪些数整除，其实质是将1001分解质因数，由1013，而且只有这一种分解结果，知道1001除了被1和它本身整除以外，还能被7、11、13整除。若把“1”也算作质数，那么将1001分解质因数就会出现下面的结果：

1001=7×11×13

1001=1×7×11×13

1001=1×1×7×111×13

……

也就是说，分解式中可随便添上几个因数“1”。这样做，一方面对求1001的因数毫无必要，另一方面分解质因质结果不唯一，又增添了不必要的麻烦。因此“1”不算作质数。