2022年河南省许昌建安区四校联考毕业升学考试模拟卷数学卷含解析

这是一份2022年河南省许昌建安区四校联考毕业升学考试模拟卷数学卷含解析，共20页。试卷主要包含了考生要认真填写考场号和座位序号，如图，直线与y轴交于点，实数4的倒数是等内容，欢迎下载使用。
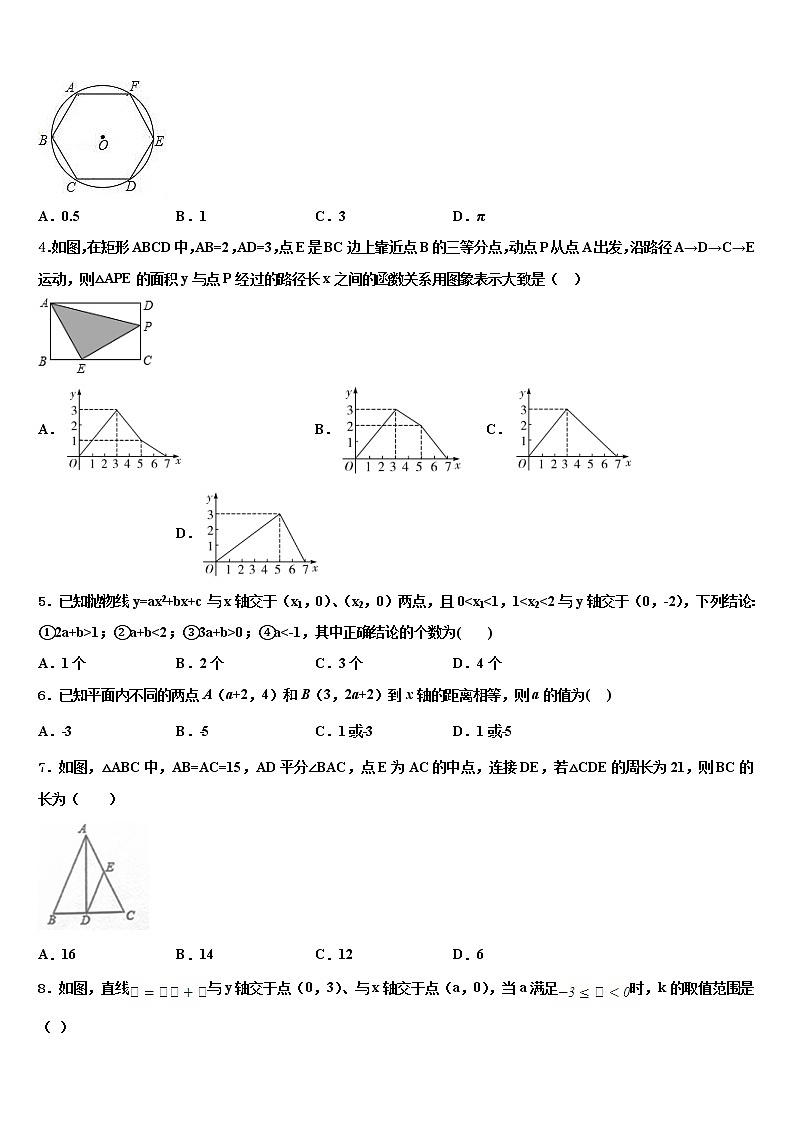
2021-2022中考数学模拟试卷注意事项1．考生要认真填写考场号和座位序号。2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。 一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1．如图 1 是某生活小区的音乐喷泉，  水流在各个方向上沿形状相同的抛物线路径落下，其中一个喷水管喷水的最大高度为 3 m，此时距喷水管的水平距离为 1 m，在如图 2 所示的坐标系中，该喷水管水流喷出的高度（m）与水平距离（m）之间的函数关系式是（    ）A． B．C． D．2．下图是由八个相同的小正方体组合而成的几何体，其左视图是（    ）A． B． C． D．3．魏晋时期的数学家刘徽首创割圆术．为计算圆周率建立了严密的理论和完善的算法．作圆内接正多边形，当正多边形的边数不断增加时，其周长就无限接近圆的周长，进而可用来求得较为精确的圆周率．祖冲之在刘徽的基础上继续努力，当正多边形的边数增加24576时，得到了精确到小数点后七位的圆周率，这一成就在当时是领先其他国家一千多年，如图，依据“割圆术”，由圆内接正六边形算得的圆周率的近似值是（　　）A．0.5 B．1 C．3 D．π4．如图，在矩形ABCD中，AB=2，AD=3，点E是BC边上靠近点B的三等分点，动点P从点A出发，沿路径A→D→C→E运动，则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是（  ）A． B． C． D．5．已知抛物线y=ax2+bx+c与x轴交于（x1，0）、（x2，0）两点，且0<x1<1，1<x2<2与y轴交于（0，-2），下列结论：①2a+b>1；②a+b<2；③3a+b>0；④a<-1，其中正确结论的个数为(    )A．1个 B．2个 C．3个 D．4个6．已知平面内不同的两点A（a+2，4）和B（3，2a+2）到x轴的距离相等，则a的值为(     )A．﹣3 B．﹣5 C．1或﹣3 D．1或﹣57．如图，△ABC中，AB=AC=15，AD平分∠BAC，点E为AC的中点，连接DE，若△CDE的周长为21，则BC的长为（    ）A．16 B．14 C．12 D．68．如图，直线与y轴交于点（0，3）、与x轴交于点（a，0），当a满足时，k的取值范围是（ ）A． B． C． D．9．实数4的倒数是（　　）A．4 B． C．﹣4 D．﹣10．如图，点ABC在⊙O上，OA∥BC，∠OAC=19°，则∠AOB的大小为（　　）A．19° B．29° C．38° D．52°二、填空题（共7小题，每小题3分，满分21分）11．如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m．水面下降2.5m，水面宽度增加_____m．12．如图，在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，BC＝4，点D是AC边上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值为___．13．为迎接五月份全县中考九年级体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一众数是13，平均数是12，那么这组数据的方差是_____．14．在直径为的圆柱形油槽内装入一些油后，截面如图所示如果油面宽，那么油的最大深度是_________．15．若函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是　   　．16．若一次函数y=﹣x+b（b为常数）的图象经过点（1，2），则b的值为_____．17．两圆内切，其中一个圆的半径长为6，圆心距等于2，那么另一个圆的半径长等于__．三、解答题（共7小题，满分69分）18．（10分）画出二次函数y＝(x﹣1)2的图象．19．（5分）如图，点O为Rt△ABC斜边AB上的一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD.求证：AD平分∠BAC；若∠BAC=60∘，OA=4，求阴影部分的面积(结果保留π).20．（8分）某区域平面示意图如图，点O在河的一侧，AC和BC表示两条互相垂直的公路．甲勘测员在A处测得点O位于北偏东45°，乙勘测员在B处测得点O位于南偏西73.7°，测得AC=840m，BC=500m．请求出点O到BC的距离．参考数据：sin73.7°≈，cos73.7°≈，tan73.7°≈21．（10分）已知：如图，在△ABC中，AB＝13，AC＝8，cos∠BAC＝，BD⊥AC，垂足为点D，E是BD的中点，联结AE并延长，交边BC于点F．（1）求∠EAD的余切值；（2）求的值．22．（10分）中华文明，源远流长；中华汉字，寓意深广．为了传承中华民族优秀传统文化，我市某中学举行“汉字听写”比赛，赛后整理参赛学生的成绩，将学生的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整．请你根据统计图解答下列问题：参加比赛的学生共有____名；在扇形统计图中，m的值为____，表示“D等级”的扇形的圆心角为____度；组委会决定从本次比赛获得A等级的学生中，选出2名去参加全市中学生“汉字听写”大赛．已知A等级学生中男生有1名，请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率．23．（12分）如图，在Rt△ABC中，∠C=90°，O为BC边上一点，以OC为半径的圆O，交AB于D点，且AD=AC，延长DO交圆O于E点，连接AE.求证：DE⊥AB；若DB=4，BC=8，求AE的长.24．（14分）如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线交AB，BC分别于点M，N，反比例函数的图象经过点M，N．求反比例函数的解析式；若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．


参考答案 一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1、D【解析】
根据图象可设二次函数的顶点式，再将点（0,0）代入即可．【详解】解：根据图象，设函数解析式为由图象可知，顶点为（1,3）∴，将点（0,0）代入得解得∴故答案为：D．【点睛】本题考查了是根据实际抛物线形，求函数解析式，解题的关键是正确设出函数解析式．2、B【解析】
解：找到从左面看所得到的图形，从左面可看到从左往右三列小正方形的个数为：2，3，1．故选B．3、C【解析】
连接OC、OD，根据正六边形的性质得到∠COD＝60°，得到△COD是等边三角形，得到OC＝CD，根据题意计算即可．【详解】连接OC、OD，∵六边形ABCDEF是正六边形，∴∠COD＝60°，又OC＝OD，∴△COD是等边三角形，∴OC＝CD，正六边形的周长：圆的直径＝6CD：2CD＝3，故选：C．【点睛】本题考查的是正多边形和圆，掌握正多边形的中心角的计算公式是解题的关键．4、B【解析】
由题意可知，当时，；当时，；当时，.∵时，；时，.∴结合函数解析式，可知选项B正确.【点睛】考点：1．动点问题的函数图象;2．三角形的面积．5、A【解析】
如图，且图像与y轴交于点，可知该抛物线的开口向下，即,①当时，  故①错误．②由图像可知，当时，∴∴故②错误．③∵∴，又∵，∴，∴，∴，故③错误；④∵，，又∵，∴．故④正确．故答案选A.【点睛】本题考查二次函数系数符号的确定由抛物线的开口方向、对称轴和抛物线与坐标轴的交点确定．6、A【解析】分析：根据点A（a＋2，4）和B（3，2a＋2）到x轴的距离相等，得到4＝|2a＋2|，即可解答．详解：∵点A（a＋2，4）和B（3，2a＋2）到x轴的距离相等，∴4＝|2a＋2|，a＋2≠3，解得：a＝−3，故选A．点睛：考查点的坐标的相关知识；用到的知识点为：到x轴和y轴的距离相等的点的横纵坐标相等或互为相反数．7、C【解析】
先根据等腰三角形三线合一知D为BC中点，由点E为AC的中点知DE为△ABC中位线，故△ABC的周长是△CDE的周长的两倍，由此可求出BC的值.【详解】∵AB=AC=15，AD平分∠BAC，∴D为BC中点，∵点E为AC的中点，∴DE为△ABC中位线，∴DE=AB，∴△ABC的周长是△CDE的周长的两倍，由此可求出BC的值.∴AB+AC+BC=42，∴BC=42-15-15=12，故选C.【点睛】此题主要考查三角形的中位线定理，解题的关键是熟知等腰三角形的三线合一定理.8、C【解析】
解：把点（0，2）（a，0）代入，得b=2．则a=，∵，∴，解得：k≥2．故选C．【点睛】本题考查一次函数与一元一次不等式，属于综合题，难度不大．9、B【解析】
根据互为倒数的两个数的乘积是1，求出实数4的倒数是多少即可．【详解】解：实数4的倒数是：1÷4=．故选：B．【点睛】此题主要考查了一个数的倒数的求法，要熟练掌握，解答此题的关键是要明确：互为倒数的两个数的乘积是1．10、C【解析】
由AO∥BC，得到∠ACB=∠OAC=19°，根据圆周角定理得到∠AOB=2∠ACB=38°.【详解】∵AO∥BC，∴∠ACB=∠OAC，而∠OAC=19°，∴∠ACB=19°，∴∠AOB=2∠ACB=38°．故选：C．【点睛】本题考查了圆周角定理与平行线的性质．解题的关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用是解此题的关键. 二、填空题（共7小题，每小题3分，满分21分）11、1.【解析】
根据已知建立平面直角坐标系，进而求出二次函数解析式，再通过把y=-1.5代入抛物线解析式得出水面宽度，即可得出答案【详解】解：建立平面直角坐标系，设横轴x通过AB，纵轴y通过AB中点O且通过C点，则通过画图可得知O为原点，
抛物线以y轴为对称轴，且经过A，B两点，OA和OB可求出为AB的一半1米，抛物线顶点C坐标为（0，1），
设顶点式y=ax1+1，把A点坐标（-1，0）代入得a=-0.5，
∴抛物线解析式为y=-0.5x1+1，
当水面下降1.5米，通过抛物线在图上的观察可转化为：
当y=-1.5时，对应的抛物线上两点之间的距离，也就是直线y=-1与抛物线相交的两点之间的距离，
可以通过把y=-1.5代入抛物线解析式得出：
-1.5=-0.5x1+1，
解得：x=±3，
1×3-4=1，
所以水面下降1.5m，水面宽度增加1米．
故答案为1．【点睛】本题考查了二次函数的应用，根据已知建立坐标系从而得出二次函数解析式是解决问题的关键，学会把实际问题转化为二次函数，利用二次函数的性质解决问题，属于中考常考题型．12、﹣2【解析】
连结AE，如图1，先根据等腰直角三角形的性质得到AB=AC=4，再根据圆周角定理，由AD为直径得到∠AED=90°，接着由∠AEB=90°得到点E在以AB为直径的 O上，于是当点O、E、C共线时，CE最小，如图2，在Rt△AOC中利用勾股定理计算出OC=2，从而得到CE的最小值为2﹣2.【详解】连结AE，如图1，∵∠BAC=90°,AB=AC,BC=，∴AB=AC=4，∵AD为直径，∴∠AED=90°，∴∠AEB=90°，∴点E在以AB为直径的O上，∵O的半径为2，∴当点O、E. C共线时,CE最小,如图2在Rt△AOC中，∵OA=2，AC=4，∴OC=，∴CE=OC−OE=2﹣2，即线段CE长度的最小值为2﹣2.故答案为:2﹣2.【点睛】此题考查等腰直角三角形的性质，圆周角定理，勾股定理，解题关键在于结合实际运用圆的相关性质.13、【解析】分析：根据已知条件得到被墨汁覆盖的三个数为：10，13，13，根据方差公式即可得到结论．详解：∵平均数是12，∴这组数据的和=12×7=84，∴被墨汁覆盖三天的数的和=84−4×12=36，∵这组数据唯一众数是13，∴被墨汁覆盖的三个数为：10，13，13， 故答案为点睛：考查方差，算术平均数，众数，根据这组数据唯一众数是13，得到被墨汁覆盖的三个数为：10，13，13是解题的关键.14、2m【解析】
本题是已知圆的直径，弦长求油的最大深度其实就是弧AB的中点到弦AB的距离，可以转化为求弦心距的问题，利用垂径定理来解决．【详解】解：过点O作OM⊥AB交AB与M，交弧AB于点E．连接OA．在Rt△OAM中：OA=5m，AM=AB=4m．根据勾股定理可得OM=3m，则油的最大深度ME为5-3=2m．【点睛】圆中的有关半径，弦长，弦心距之间的计算一般是通过垂径定理转化为解直角三角形的问题．15、0或1【解析】分析：需要分类讨论：①若m=0，则函数y=2x+1是一次函数，与x轴只有一个交点；②若m≠0，则函数y=mx2+2x+1是二次函数，根据题意得：△=4﹣4m=0，解得：m=1。∴当m=0或m=1时，函数y=mx2+2x+1的图象与x轴只有一个公共点。16、3【解析】
把点（1，2）代入解析式解答即可．【详解】解：把点（1，2）代入解析式y=-x+b，可得：2=-1+b，解得：b=3，故答案为3【点睛】本题考查的是一次函数的图象点的关系，关键是把点（1，2）代入解析式解答．17、4或1【解析】∵两圆内切，一个圆的半径是6，圆心距是2，∴另一个圆的半径=6-2=4；或另一个圆的半径=6+2=1，故答案为4或1．【点睛】本题考查了根据两圆位置关系来求圆的半径的方法．注意圆的半径是6，要分大圆和小圆两种情况讨论． 三、解答题（共7小题，满分69分）18、见解析【解析】
首先可得顶点坐标为（1，0），然后利用对称性列表，再描点，连线，即可作出该函数的图象．【详解】列表得：x…﹣10123…y…41014…如图：．【点睛】此题考查了二次函数的图象．注意确定此二次函数的顶点坐标是关键．19、（1）见解析；（2）【解析】试题分析：（1）连接OD，则由已知易证OD∥AC，从而可得∠CAD=∠ODA，结合∠ODA=∠OAD，即可得到∠CAD=∠OAD，从而得到AD平分∠BAC；（2）连接OE、DE，由已知易证△AOE是等边三角形，由此可得∠ADE=∠AOE=30°，由AD平分∠BAC可得∠OAD=30°，从而可得∠ADE=∠OAD，由此可得DE∥AO，从而可得S阴影=S扇形ODE，这样只需根据已知条件求出扇形ODE的面积即可.试题解析：（1）连接OD.∵BC是⊙O的切线，D为切点，∴OD⊥BC. 又∵AC⊥BC，∴OD∥AC，∴∠ADO=∠CAD.又∵OD=OA，∴∠ADO=∠OAD，∴∠CAD=∠OAD，即AD平分∠BAC. （2）连接OE，ED.∵∠BAC=60°，OE=OA，∴△OAE为等边三角形，∴∠AOE=60°，∴∠ADE=30°. 又∵，∴∠ADE=∠OAD，∴ED∥AO， ∴S△AED＝S△OED，∴阴影部分的面积 = S扇形ODE = .20、点O到BC的距离为480m．【解析】
作OM⊥BC于M，ON⊥AC于N，设OM=x，根据矩形的性质用x表示出OM、MC，根据正切的定义用x表示出BM，根据题意列式计算即可．【详解】作OM⊥BC于M，ON⊥AC于N，则四边形ONCM为矩形，∴ON=MC，OM=NC，设OM=x，则NC=x，AN=840﹣x，在Rt△ANO中，∠OAN=45°，∴ON=AN=840﹣x，则MC=ON=840﹣x，在Rt△BOM中，BM==x，由题意得，840﹣x+x=500，解得，x=480，答：点O到BC的距离为480m．【点睛】本题考查的是解直角三角形的应用，掌握锐角三角函数的定义、正确标注方向角是解题的关键．21、（1）∠EAD的余切值为；（2）=.【解析】
（1）在Rt△ADB中，根据AB=13，cos∠BAC=，求出AD的长，由勾股定理求出BD的长，进而可求出DE的长，然后根据余切的定义求∠EAD的余切即可；（2）过D作DG∥AF交BC于G，由平行线分线段成比例定理可得CD：AD=CG：FG=3:5，从而可设CD=3x，AD=5x，再由EF∥DG，BE=ED， 可知BF=FG=5x，然后可求BF：CF的值.【详解】（1）∵BD⊥AC，∴∠ADE=90°，Rt△ADB中，AB=13，cos∠BAC=，∴AD=5，  由勾股定理得：BD=12，∵E是BD的中点，  ∴ED=6，  ∴∠EAD的余切==；（2）过D作DG∥AF交BC于G，∵AC=8，AD=5，  ∴CD=3，∵DG∥AF，  ∴=，设CD=3x，AD=5x，∵EF∥DG，BE=ED，  ∴BF=FG=5x，∴==.【点睛】本题考查了勾股定理，锐角三角函数的定义，平行线分线段成比例定理.解（1）的关键是熟练掌握锐角三角函数的概念，解（2）的关键是熟练掌握平行线分线段成比例定理.22、（1）20；（2）40，1；（3）．【解析】试题分析：（1）根据等级为A的人数除以所占的百分比求出总人数；（2）根据D级的人数求得D等级扇形圆心角的度数和m的值；（3）列表得出所有等可能的情况数，找出一男一女的情况数，即可求出所求的概率．试题解析：解：（1）根据题意得：3÷15%=20（人），故答案为20；（2）C级所占的百分比为×100%=40%，表示“D等级”的扇形的圆心角为×360°=1°；故答案为40、1．（3）列表如下：所有等可能的结果有6种，其中恰好是一名男生和一名女生的情况有4种，则P恰好是一名男生和一名女生= =．23、（1）详见解析；（2）6【解析】
（1）连接CD，证明即可得到结论；（2）设圆O的半径为r，在Rt△BDO中，运用勾股定理即可求出结论.【详解】（1）证明：连接CD,∵∴∵∴.（2）设圆O的半径为，，设.【点睛】本题综合考查了切线的性质和判定及勾股定理的综合运用．综合性比较强，对于学生的能力要求比较高．24、（1）；（2）点P的坐标是（0，4）或（0，－4）.【解析】
（1）求出OA=BC=2，将y=2代入求出x=2，得出M的坐标，把M的坐标代入反比例函数的解析式即可求出答案.（2）求出四边形BMON的面积，求出OP的值，即可求出P的坐标.【详解】（1）∵B（4，2），四边形OABC是矩形，∴OA=BC=2.将y=2代入3得：x=2，∴M（2，2）.把M的坐标代入得：k=4，∴反比例函数的解析式是；（2）.∵△OPM的面积与四边形BMON的面积相等，∴.∵AM=2，∴OP=4.∴点P的坐标是（0，4）或（0，－4）.