2022年安徽省合肥市蜀山区重点中学中考数学全真模拟试卷含解析

这是一份2022年安徽省合肥市蜀山区重点中学中考数学全真模拟试卷含解析，共25页。试卷主要包含了若a+b=3，，则ab等于等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．如图，在△ABC中，∠C＝90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC＝6，NC＝，则四边形MABN的面积是（ ）

A． B． C． D．
2．如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD=．其中正确的结论有（　　）

A．4个 B．3个 C．2个 D．1个
3．关于的不等式的解集如图所示，则的取值是　　

A．0 B． C． D．
4．下列各式属于最简二次根式的有（ ）
A． B． C． D．
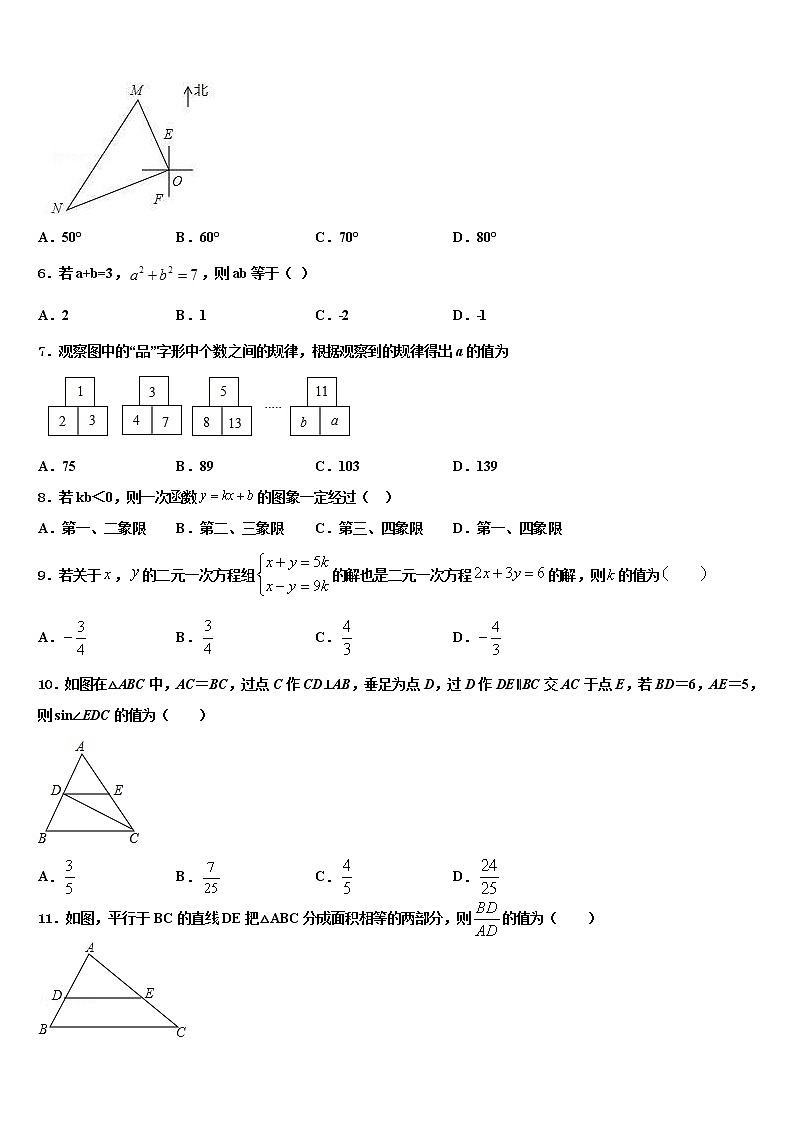
5．一艘轮船和一艘渔船同时沿各自的航向从港口O出发，如图所示，轮船从港口O沿北偏西20°的方向行60海里到达点M处，同一时刻渔船已航行到与港口O相距80海里的点N处，若M、N两点相距100海里，则∠NOF的度数为（ ）

A．50° B．60° C．70° D．80°
6．若a+b=3，，则ab等于（ ）
A．2 B．1 C．﹣2 D．﹣1
7．观察图中的“品”字形中个数之间的规律，根据观察到的规律得出a的值为

A．75 B．89 C．103 D．139
8．若kb＜0，则一次函数的图象一定经过（ ）
A．第一、二象限 B．第二、三象限 C．第三、四象限 D．第一、四象限
9．若关于，的二元一次方程组的解也是二元一次方程的解，则的值为　　
A． B． C． D．
10．如图在△ABC中，AC＝BC，过点C作CD⊥AB，垂足为点D，过D作DE∥BC交AC于点E，若BD＝6，AE＝5，则sin∠EDC的值为（　　）

A． B． C． D．
11．如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则的值为（　　）

A．1 B． C．-1 D．+1
12．的值是　　
A．±3 B．3 C．9 D．81
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．已知线段厘米，厘米，线段c是线段a和线段b的比例中项，线段c的长度等于________厘米．
14．如果一个矩形的面积是40，两条对角线夹角的正切值是，那么它的一条对角线长是__________．
15．因式分解：3x2-6xy+3y2=______．
16．国家游泳中心“水立方”是奥运会标志性建筑之一，其工程占地面积约为62800m2，将62800用科学记数法表示为_____．
17．关于的方程有两个不相等的实数根，那么的取值范围是__________．
18．将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，若∠ABE＝20°，则∠DBC为_____度．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）未成年人思想道德建设越来越受到社会的关注，辽阳青少年研究所随机调查了本市一中学100名学生寒假中花零花钱的数量(钱数取整数元)，以便引导学生树立正确的消费观．根据调查数据制成了频
分组
频数
频率
0.5～50.5
　 　
0.1
50.5～　 　
20
0.2
100.5～150.5
　 　
　 　
　 　200.5
30
0.3
200.5～250.5
10
0.1
率分布表和频率分布直方图(如图)．

(1)补全频率分布表；
(2)在频率分布直方图中，长方形ABCD的面积是　 　；这次调查的样本容量是　 　；
(3)研究所认为，应对消费150元以上的学生提出勤俭节约的建议．试估计应对该校1000名学生中约多少名学生提出这项建议．
20．（6分）某高校学生会在某天午餐后，随机调查了部分同学就餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．

（1）这次被调查的同学共有名；
（2）补全条形统计图；
（3）计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数；
（4）校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐．据此估算，该校20000名学生一餐浪费的食物可供多少人食用一餐？
21．（6分）某超市在春节期间开展优惠活动，凡购物者可以通过转动转盘的方式享受折扣和优惠，在每个转盘中指针指向每个区域的可能性均相同，若指针指向分界线，则重新转动转盘，区域对应的优惠方式如下，A1，A2，A3区域分别对应9折8折和7折优惠，B1，B2，B3，B4区域对应不优惠？本次活动共有两种方式．
方式一：转动转盘甲，指针指向折扣区域时，所购物品享受对应的折扣优惠，指针指向其他区域无优惠；
方式二：同时转动转盘甲和转盘乙，若两个转盘的指针均指向折扣区域时，所购物品享受折上折的优惠，其他情况无优惠．
（1）若顾客选择方式一，则享受优惠的概率为　 　；
（2）若顾客选择方式二，请用树状图或列表法列出所有可能顾客享受折上折优惠的概率．

22．（8分）如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=1OD，OE=1OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．

（1）求证：DE⊥AG；
（1）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图1．
①在旋转过程中，当∠OAG′是直角时，求α的度数；
②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．
23．（8分）甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线OBCDA表示轿车离甲地距离y（千米）与时间x（小时）之间的函数关系．请根据图象解答下列问题：当轿车刚到乙地时，此时货车距离乙地　 　千米；当轿车与货车相遇时，求此时x的值；在两车行驶过程中，当轿车与货车相距20千米时，求x的值．

24．（10分）抛物线y=ax2+bx+3（a≠0）经过点A（﹣1，0），B（，0），且与y轴相交于点C．
（1）求这条抛物线的表达式；
（2）求∠ACB的度数；
（3）点D是抛物线上的一动点，是否存在点D，使得tan∠DCB=tan∠ACO．若存在，请求出点D的坐标，若不存在，说明理由．

25．（10分）随着交通道路的不断完善，带动了旅游业的发展，某市旅游景区有A、B、C、D、E等著名景点，该市旅游部门统计绘制出2017年“五•一”长假期间旅游情况统计图，根据以下信息解答下列问题：

（1）2017年“五•一”期间，该市周边景点共接待游客 万人，扇形统计图中A景点所对应的圆心角的度数是 ，并补全条形统计图．
（2）根据近几年到该市旅游人数增长趋势，预计2018年“五•一”节将有80万游客选择该市旅游，请估计有多少万人会选择去E景点旅游？
（3）甲、乙两个旅行团在A、B、D三个景点中，同时选择去同一景点的概率是多少？请用画树状图或列表法加以说明，并列举所用等可能的结果．
26．（12分）已知开口向下的抛物线y=ax2-2ax+2与y轴的交点为A，顶点为B，对称轴与x轴的交点为C，点A与点D关于对称轴对称，直线BD与x轴交于点M，直线AB与直线OD交于点N．
(1)求点D的坐标.
(2)求点M的坐标(用含a的代数式表示).
(3)当点N在第一象限，且∠OMB=∠ONA时，求a的值．

27．（12分）已知平行四边形．
尺规作图：作的平分线交直线于点，交延长线于点（要求：尺规作图，保留作图痕迹，不写作法）；在（1）的条件下，求证：．



参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、C
【解析】
连接CD，交MN于E，
∵将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，
∴MN⊥CD，且CE=DE．∴CD=2CE．
∵MN∥AB，∴CD⊥AB．∴△CMN∽△CAB．
∴．
∵在△CMN中，∠C=90°，MC=6，NC=，∴
∴．
∴．故选C．
2、A
【解析】
①正确．只要证明∠EAC=∠ACB，∠ABC=∠AFE=90°即可；
②正确．由AD∥BC，推出△AEF∽△CBF，推出=，由AE=AD=BC，推出=，即CF=2AF；
③正确．只要证明DM垂直平分CF，即可证明；
④正确．设AE=a，AB=b，则AD=2a，由△BAE∽△ADC，有 =，即b=a，可得tan∠CAD===．
【详解】
如图，过D作DM∥BE交AC于N．
∵四边形ABCD是矩形，∴AD∥BC，∠ABC=90°，AD=BC，∴∠EAC=∠ACB．
∵BE⊥AC于点F，∴∠ABC=∠AFE=90°，∴△AEF∽△CAB，故①正确；
∵AD∥BC，∴△AEF∽△CBF，∴=．
∵AE=AD=BC，∴=，∴CF=2AF，故②正确；
∵DE∥BM，BE∥DM，∴四边形BMDE是平行四边形，∴BM=DE=BC，∴BM=CM，∴CN=NF．
∵BE⊥AC于点F，DM∥BE，∴DN⊥CF，∴DM垂直平分CF，∴DF=DC，故③正确；
设AE=a，AB=b，则AD=2a，由△BAE∽△ADC，有 =，即b=a，∴tan∠CAD===．故④正确．
故选A．

【点睛】
本题考查了相似三角形的判定和性质，矩形的性质，图形面积的计算以及解直角三角形的综合应用，正确的作出辅助线构造平行四边形是解题的关键．解题时注意：相似三角形的对应边成比例．
3、D
【解析】
首先根据不等式的性质，解出x≤，由数轴可知，x≤-1，所以=-1，解出即可；
【详解】
解：不等式，
解得x