2021-2022学年湖北省武汉市江汉区八年级（下）期末数学试卷（含解析）

这是一份2021-2022学年湖北省武汉市江汉区八年级（下）期末数学试卷（含解析），共23页。试卷主要包含了5x−1，1，s乙2=6，则平行四边形ABCD的面积是，其中正确结论的个数是，其中正确的结论是______．，【答案】A，【答案】B，【答案】D等内容，欢迎下载使用。

一．选择题（本题共10小题，共30分）
要使式子a+2有意义，a的取值范围是( )
A. a<−2B. a>−2C. a≤−2D. a≥−2
下列函数中，是正比例函数的是( )
A. y=−8xB. y=−8xC. y=5x2+6D. y=−0.5x−1
下列各组数中，为勾股数的是( )
A. 3，4，5B. 2，3，4
C. 3，4，5D. 13，14，15
方程(x+1)2=9的解为( )
A. x1=2，x2=−4B. x1=−2，x2=4
C. x1=4，x2=2D. x1=−2，x2=−4
如图，平行四边形ABCD的对角线AC，BD相交于点O，且AC+BD=34，AB=10，则△OCD的周长是( )
A. 44B. 27C. 34D. 17
某同学对甲、乙、丙、丁四个市场五月份每天的蔬菜价格进行了调查，计算后发现这个月四个市场的价格平均值相同，方差分别为s甲2=8.1，s乙2=6.3，s丙2=9.7，s丁2=7.2.则五月份蔬菜价格最稳定的市场是( )
A. 甲B. 乙C. 丙D. 丁
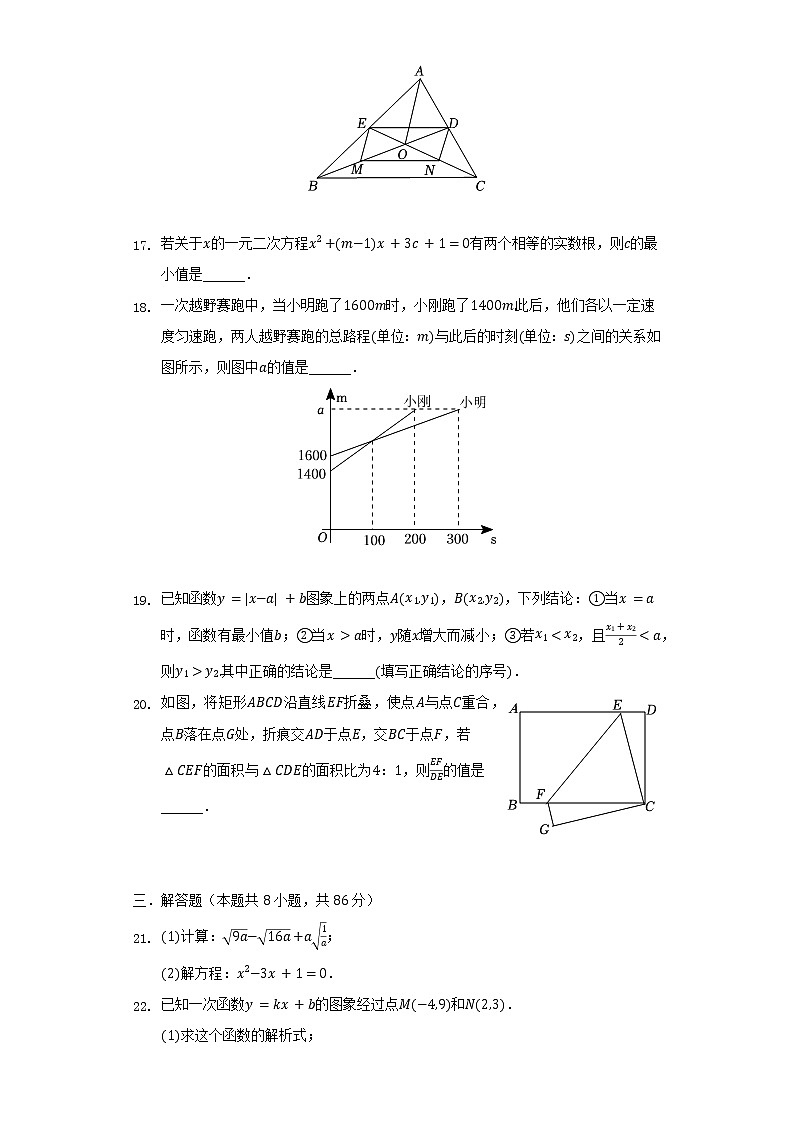
若15−n是整数，则正整数n不可能是( )
A. 6B. 9C. 11D. 14
对于一次函数y=12x−3的描述不正确的是( )
A. y随x的增大而增大B. 图象与y轴的交点是(0,−3)
C. 图象经过点(−2,−1)D. 图象不经过第二象限
▱ABCD的对角线AC，BD相交于点O，△OAB是等边三角形，且AB=3.则平行四边形ABCD的面积是( )
A. 33B. 63C. 9D. 93
下列结论：①若P1(x1,y1)，P2(x2,y2)在直线y=kx+b(k<0)上，且x1>x2，则y1>y2；②若直线y=kx+b经过第一、二、三象限，则k>0，b>0；③若一次函数y=(m−1)x+m2+2的图象交y轴于点A(0,3)，则m=±1.其中正确结论的个数是( )
0B. 1C. 2D. 3
二．填空题（本题共10小题，共34分）
二次根式32化成最简二次根式是______．
将直线y=3x−1向上平移两个单位长度后，得到的直线解析式是______．
在一次中学生田径运动会上，参加男子跳高的10名运动员的成绩如表所示：
则这些运动员成绩的平均数是______．
一元二次方程x2−2x+m=0的一个根是−2，则另一个根是______．
如图，直线y=kx+b与x轴交于点A(−3,0)，与直线y=mx+n交于点P(1,3)，则不等式0如图，在△ABC中，BD，CE分别是边AC，AB上的中线，BD与CE相交于点O，M，N分别是OB，OC的中点，连接ED，EM，MN，DN，AO.若四边形DEMN的周长为10，BC=7，则AO的长是______．
若关于x的一元二次方程x2+(m−1)x+3c+1=0有两个相等的实数根，则c的最小值是______．
一次越野赛跑中，当小明跑了1600m时，小刚跑了1400m.此后，他们各以一定速度匀速跑，两人越野赛跑的总路程(单位：m)与此后的时刻(单位：s)之间的关系如图所示，则图中a的值是______．
已知函数y=|x−a|+b图象上的两点A(x1,y1)，B(x2,y2)，下列结论：①当x=a时，函数有最小值b；②当x>a时，y随x增大而减小；③若x1y2.其中正确的结论是______(填写正确结论的序号)．
如图，将矩形ABCD沿直线EF折叠，使点A与点C重合，点B落在点G处，折痕交AD于点E，交BC于点F，若△CEF的面积与△CDE的面积比为4：1，则EFDE的值是______．
三．解答题（本题共8小题，共86分）
(1)计算：9a−16a+a1a；
(2)解方程：x2−3x+1=0．
已知一次函数y=kx+b的图象经过点M(−4,9)和N(2,3)．
(1)求这个函数的解析式；
(2)已知第一象限内的点P在直线MN上，点A(3,0)，若△OPA的面积为6，求P点坐标．
某校800名学生参加植树活动，要求每人植树4～7棵，活动结束后抽查了部分学生每人的植树量，并分为四类：A类4棵，B类5棵，C类6棵，D类7棵，将各类的人数绘制成如图所示的不完整的条形统计图和扇形统计图．
(1)被抽查的学生人数为______，将条形统计图补充完整；
(2)被抽查的学生每人植树量的众数是______，中位数是______；
(3)该校800名学生中植树6棵及以上的估计有多少人？
如图，已知四边形ABCD的对角线AC、BD交于点O，AO=OC，OB=OD且∠1=∠2．
(1)求证：四边形ABCD是菱形；
(2)E为AO上一点，连接BE，若AE=4，AB=6，EB=23，求AO的长．
如图是边长为1的小正方形组成的5×8网格，每个小正方形的顶点叫做格点．△ABC的顶点均在格点上．
(1)直接写出△ABC的形状；
(2)仅用无刻度的直尺画图(画图结果用实线，画图过程用虚线)：
①在图(1)中的AB上画点D，连接CD，使CD=AD；
②在图(1)中的AC上画点E，连接DE，使DE=10；
③在图(2)中的BC上画点G，使∠BAG=45°．
某中学计划租用客车送312名学生和8名教师集体外出活动，每辆客车上至少要有1名教师．现有甲、乙两种型号的客车，它们的载客量和租金如表所示．设租车总费用为y元，租用甲型客车x辆．
(1)共需租______辆客车；
(2)若学校计划租车总费用在3200元的限额内，求y关于x的函数解析式，并求出自变量x的取值范围；
(3)因燃油价格上涨，甲型客车每辆租金上调m元，乙型客车每辆租金上调2m元(m>0)，若租车的最低费用是3200元，求m的值．
已知：正方形ABCD中，点E在对角线BD上，连接CE，作EF⊥CE交AB于点F．
(1)如图(1)，求证：CE=EF；
(2)如图(2)，作EM⊥BD交AD于点M，连接BM.求证：BM=2CE；
(3)如图(3)，延长CE交DA于点N，若BE=72，AN=6，则CE=______．
已知，直线l：y=kx−k+3经过第一象限内的定点P．
(1)求点P的坐标；
(2)如图(1)，已知点A(2,t)，过点A作AB//y轴，交直线l于点B，连接OB，若BP平分∠OBA，求k的值；
(3)如图(2)，点Q是x轴上的一动点，连接PQ，以PQ为腰作等腰△PQR(P,Q,R按逆时针顺序排列)，∠QPR=120°，连接OR，请直接写出3OR+QR的最小值．
答案和解析
1.【答案】D
【解析】解：由题意得，a+2≥0，
解得a≥−2．
故选：D．
根据被开方数大于等于0列式计算即可得解．
本题考查了二次根式的意义，二次根式中的被开方数必须是非负数，否则二次根式无意义．
2.【答案】A
【解析】解：A、y=−8x是正比例函数，故本选项正确；
B、y=−8x，自变量x在分母上，不是正比例函数，故本选项错误；
C、y=5x2+6，自变量x的指数是2，不是1，不是正比例函数，故本选项错误；
D、y=−0.5x−1，是一次函数，不是正比例函数，故本选项错误．
故选：A．
根据正比例函数的定义，y=kx(k≠0)，对各选项分析判断后利用排除法求解．
本题考查了正比例函数的定义，解题关键是掌握正比例函数y=kx的定义条件：k为常数且k≠0，自变量次数为1．
3.【答案】A
【解析】解：A、∵32+42=52，
∴3，4，5是一组勾股数，本选项符合题意；
B、∵22+32≠42，
∴2，3，4不是一组勾股数，本选项不符合题意；
C、∵(3)2+(4)2≠(5)2，
∴3，4，5不是一组勾股数，本选项不符合题意；
D、∵132+142≠152，
∴13，14，15不是一组勾股数，本选项不符合题意；
故选：A．
根据勾股数的概念判断即可．
本题考查的是勾股数，满足a2+b2=c2 的三个正整数，称为勾股数．
4.【答案】A
【解析】解：(x+1)2=9，
x+1=±3，
所以x1=2，x2=−4．
故选：A．
把方程两边开方得到x+1=±3，然后解两个一次方程即可．
本题考查了解一元二次方程−直接开平方法：形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程．
5.【答案】B
【解析】解：∵四边形ABCD是平行四边形，
∴AO=CO，BO=DO，AB=CD=10，
∵AC+BD=34，
∴CO+DO=17，
∴△OCD的周长=OC+OD+CD=27，
故选：B．
由平行四边形的性质可得AO=CO，BO=DO，AB=CD=10，即可求解．
本题考查了平行四边形的性质，掌握平行四边形的对角线的性质是解题的关键．
6.【答案】B
【解析】解：∵四个市场的价格平均值相同，s甲2=8.1，s乙2=6.3，s丙2=9.7，s丁2=7.2，
∴方差最小的为乙市场，
∴五月份蔬菜价格最稳定的市场是乙．
故选：B．
从平均成绩以及方差分别分析，综合两个方面得出答案．
此题主要考查了方差和平均数，关键是掌握方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
7.【答案】B
【解析】解：∵15−n是整数，n为正整数，
∴15−n>0，解得：n<15，
∵15−n是整数，
∴n的值为：6，11，14，
故选：B．
先确定n的取值范围，再利用15−n是整数，n为正整数，确定n的值即可．
本题考查了算术平方根，确定n的取值范围是解题的关键．
8.【答案】C
【解析】解：A、由于一次函数y=12x−3中的k=12>0，所以y随x的增大而增大，故A正确，不符合题意；
B、一次函数y=12x−3，令x=0可得y=−3，函数图象与y轴的交点坐标为(0,−3)，故B正确，不符合题意；
C、由于一次函数y=12x−3，令x=−2可得y=−4，函数图象与y轴的交点坐标为(−2,−4)，故C不正确，符合题意；
D、一次函数y=12x−3，k=12>0，b=−3<0，所以函数图象经过第一、三、四象限，不经过第二象限，故D正确，不符合题意．
故选：C．
根据一次函数图象的性质，一次函数图象上点的坐标特征，一次函数图象与直线的交点进行分析判断即可．
本题考查了一次函数图象上点的坐标特征以及一次函数的性质，掌握一次函数的增减性、与坐标轴的交点坐标是解题的关键．
9.【答案】D
【解析】解：∵△AOB是等边三角形，AB=3，
∴S△AOB=34×9=934，
∵四边形ABCD是平行四边形，
∴S▱ABCD=4S△AOB=93，
故选：D．
先求出等边三角形OAB的面积，由平行四边形的性质可求解．
本题考查了平行四边形的性质，掌握平行四边形的性质是解题的关键．
10.【答案】B
【解析】解：①∵k<0，
∴y随x的增大而减小，
又∵若P1(x1,y1)，P2(x2,y2)在直线y=kx+b(k<0)上，且x1>x2，
∴y1∴①不正确；
②当直线y=kx+b经过第一、三象限时，k>0，b=0；
当直线y=kx+b经过第一、二、三象限时，k>0，b>0，
∴②正确；
③∵一次函数y=(m−1)x+m2+2的图象交y轴于点A(0,3)，
∴m−1≠0m2+2=3，
解得：m=−1，
∴结论③不正确．
∴正确的结论只有1个．
故选：B．
根据一次函数的图象和性质，这个选项进行判断，最后得出答案．
本题考查了一次函数图象上点的坐标特征、一次函数图象与系数的关系、一次函数的性质以及一次函数的定义，逐一分析各个结论的正误是解题的关键．
11.【答案】42
【解析】解：32=42．
故答案为：42．
直接利用二次根式的性质化简得出答案．
此题主要考查了最简二次根式，正确化简二次根式是解题关键．
12.【答案】y=3x+1
【解析】
【分析】
本题考查的是一次函数的图象与几何变换，熟知函数解析式“上加下减”的原则是解答此题的关键.根据函数解析式“上加下减”的原则进行解答即可．
【解答】
解：由“上加下减”的原则可知，
将直线y=3x−1向上平移2个单位长度，得到的一次函数解析式为y=3x−1+2，即y=3x+1．
故答案为y=3x+1．
13.【答案】1.64
【解析】解：根据题意得：
110×(1.50×2+1.60×3+1.70×4+1.80)=1.64(m)，
答：这些运动员成绩的平均数是1.64．
故答案为：1.64．
根据加权平均数的计算公式列出算式，再进行计算即可得出答案．
本题考查的是加权平均数的求法，熟练掌握加权平均数的计算公式是解题的关键．
14.【答案】4
【解析】解：设另一个根为x，
∵一元二次方程x2−2x+m=0的一个根是−2，
∴−2+x=−(−2)，
解得x=4，
∴另一个根为4，
故答案为：4．
设另一个根为x，根据根与系数的关系列方程即可求解．
本题考查了一元二次方程，熟练掌握根与系数的关系是解题的关键．
15.【答案】−3【解析】解：根据图象可知，不等式0故答案为：−3根据图象即可确定不等式组的解集．
本题考查了一次函数与一元一次不等式的关系，熟练掌握一次函数图象是解题的关键．
16.【答案】3
【解析】解：∵BD，CE分别是边AC，AB上的中线，
∴DE=12BC=72，DE//BC，
∵M，N分别是OB，OC的中点，
MN=12BC=72，MN//BC，
∴DE=MN，DE//MN，
∴四边形DEMN为平行四边形，
∴ME=DN，
∵四边形DEMN的周长为10，BC=7，
∴ME=DN=32，
∵CE是边AB上的中线，M是OB的中点，
∴AO=2ME=3．
故答案为：3．
根据三角形中位线定理得到DE=12BC=72，DE//BC，MN=12BC=72，MN//BC，得到四边形DEMN为平行四边形，可得ME=DN=32，根据三角形中位线定理即可得AO=2ME=3．
本题考查的是三角形中位线定理、平行四边形的判定和性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
17.【答案】−13
【解析】解：∵关于x的一元二次方程x2+(m−1)x+3c+1=0有两个相等的实数根，
∴Δ=(m−1)2−4(3c+1)=0，
∴c=112(m−1)2−13，
∵(m−1)2≥0，
∴c的最小值为−13．
故答案为：−13．
根据根的判别式的意义得到m−1)2−4(3c+1)=0，再用m表示c得到c=112(m−1)2−13，然后根据非负数的性质确定c的最小值．
本题考查了根的判别式：一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系：当Δ>0时，方程有两个不相等的实数根；当Δ=0时，方程有两个相等的实数根；当Δ<0时，方程无实数根．
18.【答案】2200
【解析】解：设小明的速度为a m/s，小刚的速度为b m/s，根据题意得：
1600+100a=1400+100b1600+300a=1400+200b，
解答a=2b=4，
故a=1600+300×2=2200．
故答案为：2200．
设小明的速度为a m/s，小刚的速度为b m/s，根据题意列方程组解答即可．
本题考查了函数的图象，根据题意列出方程组是解答本题的关键．
19.【答案】①③
【解析】解：在函数y=|x−a|+b中，
∵|x−a|≥0，
当x=a时，y取得最小值b，
故①选项符合题意；
由①可知，当x>a时，y随着x增大而增大，
故②选项不符合题意；
∵x1∴x2−a∵当x=a时，y取得最小值b，
∴y1>y2，
故③选项符合题意，
综上，正确的选项有①③，
故答案为：①③．
根据绝对值的性质可判断①选项，根据①选项以及一次函数的性质即可判断②③选项．
本题考查了一次函数的性质，熟练掌握绝对值的性质以及一次函数的性质是解题的关键．
20.【答案】26
【解析】解：连接AF，由翻折知，△AEF≌△CEF，
∴∠AEF=∠CEF，
∵AE//CF，
∴∠AEF=∠EFC，
∴∠AFE=∠AEF=∠CFE=∠CEF，
∴AF=AE=CE=CF，
∵△CEF的面积与△CDE的面积比为4：1，
∴△AEF的面积与△CDE的面积比为4：1，
∴AE：ED=4：1，
设DE=x，则AE=CE=CF=4x，
作EH⊥CF于H，

∴FH=3x，
∵EH=CE2−ED2=15x，
∴EF=FH2+EH2=26x，
∴EFDE=26xx=26，
故答案为：26．
连接AF，由翻折知，△AEF≌△CEF，由面积比得出AE：ED=4：1，设DE=x，则AE=CE=4x，作EH⊥CF于H，利用勾股定理求出EF即可得出比值．
本题主要考查矩形的性质，三角形的面积，勾股定理等知识，熟练掌握矩形的性质，三角形的面积，勾股定理等知识是解题的关键．
21.【答案】解：(1)原式=3a−4a+a
=0；
(2)∵a=1，b=3，c=1，
∴Δ=b2−4ac=32−4×1×1=5>0，
∴x=3±52×1，
∴x1=3+52，x2=3−52．
【解析】(1)先把各二次根式化为最简二次根式，然后合并即可；
(2)先计算出根的判别式的值，然后利用求根公式得到方程的解．
本题考查了解一元二次方程−公式法：用求根公式解一元二次方程的方法是公式法．熟练掌握用公式法解一元二次方程的一般步骤是解决问题的关键．也考查了二次根式的加减法．
22.【答案】解：(1)根据题意得−4k+b=92k+b=3，
解得k=−1b=5，
所以一次函数解析式为y=−x+5；
(2)设点P(m,−m+5)，
∵点A(3,0)，
∴OA=3，
∵△OPA的面积为6，
∴△OPA的面积=12×AO×(−m+5)=6，
∴12×3×(−m+5)=6，
∴m=1，
∴点P(1,4)．
【解析】(1)利用待定系数法求得即可；
(2)设点P(m,−m+5)，利用△OPA的面积=12×AO×(−m+5)=6，求出m即可求解．
本题考查了待定系数法求一次函数解析式，函数图象上点的坐标特征，三角形的面积．求出一次函数解析式是解题的关键．
23.【答案】40 6棵 6棵
【解析】解：(1)被抽查的学生人数有：3÷7.5%=40(人)，
C类的人数为：40×42.5%=17(人)，
补全统计图如图所示：

(2)由图可知，植树6棵的人数最多，是17人，
所以，众数为6棵，
按照植树的棵树从少到多排列，第20人与第21人都是植6棵数，
所以，中位数是6棵；
故答案为：6棵，6棵；
(3)根据题意得：
800×17+1240=580(棵)，
答：该校800名学生中植树6棵及以上的估计有580棵．
(1)根据A的人数和所占的百分比，求出总人数，再用总人数乘以C类所占的百分比，求出C类的人数，然后补全统计图即可；
(2)根据众数和中位数的定义进行解答即可；
(3)用该校的总人数乘以植树6棵及以上的人数所占的百分比即可．
本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．
24.【答案】(1)证明：∵AO=OC，OB=OD，
∴四边形ABCD是平行四边形，
∴AD//BC，
∴∠2=∠ACB，
∵∠1=∠2，
∴∠1=∠ACB
∴AB=CB，
∴平行四边形ABCD是菱形；
(2)解：∵四边形ABCD是菱形，
∴AC⊥BD，
在Rt△ABO和Rt△EBO中，根据勾股定理得：OB2=AB2−AO2=BE2−OE2，
设OE=x，
∵AE=4，AB=6，EB=23，AO=4+x，
∴62−(4+x)2=(23)2−x2，
解得：x=1，
∴AO=AE+OE=4+1=5．
【解析】(1)根据AO=OC，OB=OD，可得四边形ABCD是平行四边形，然后证明AB=CB，进而可以解决问题；
(2)根据菱形的对角线互相垂直，设OE=x，利用勾股定理求出x的值，进而可以解决问题．
本题考查了菱形的判定与性质，平行四边形的判定与性质，等腰三角形的判定以及勾股定理等知识，解决本题的关键是掌握菱形的判定与性质．
25.【答案】解：(1)∵AC=32+32=32，BC=42+42=42，AB=72+12=52，
∴AC2+BC2=AB2，
∴∠ACB=90°，
∴△ABC是直角三角形．
(2)①如图(1)中，点D即为所求；
②如图(1)中，点E或点E′即为所求；
③如图②中，点G即为所求．

【解析】(1)利用勾股定理的逆定理判断即可；
(2)①作线段BC的垂直平分线交AB于点D，点D即为所求；
②设AC的垂直平分线交AC于点R，在RC或RA上，截取RE=2或RE′=2，连接DE，DE′即可；
③取格点T，漏解AT几艘BC于点G，点G即为所求．
本题考查作图−应用与设计作图，勾股定理，线段的垂直平分线的性质等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．
26.【答案】8
【解析】解：(1)如果全部租用甲种客车，则需要(312+8)÷45=719(辆)，
如果全部租用乙种客车，则需要(312+8)÷30=1023(辆)，
∵汽车辆数为整数，且有8名教师，每辆汽车上至少要有1名教师，
∴共需租8辆汽车．
故答案为：8；
(2)设租用x辆甲种客车，则租用乙种客车(8−x)辆，
则租车费用y=400x+280(8−x)=120x+2240，
∵45x+30(8−x)≥320400x+280(8−x)≤3200，
解得513≤x≤8，
∵x为整数，
∴x=6或7或8．
故y关于x的函数解析式是y=120x+2240，自变量x的取值范围是x=6或7或8；
(3)依题意有：(400+m)x+(280+2m)(8−x)=3200，
解得x=8−8m120−m，
∵x为整数，
∴m=24或40或56．
故m的值为24或40或56．
(1)根据题意和表格中的数据可以得到需要租用多少辆客车，本题得以解决；
(2)根据(1)中的结果和表格中的数据可以得到y关于x的函数解析式，以及自变量x的取值范围；
(3)根据租车的最低费用是3200元，列出不等式可求m的值．
本题考查一次函数的应用、一元一次不等式组的应用，一元二次方程的应用，解答本题的关键是明确题意，利用一次函数的性质和不等式的性质解答．
27.【答案】214
【解析】(1)证明：如图，过点E作EH⊥BC于H，EG⊥AB于G，

∵四边形ABCD是正方形，
∴∠ABD=∠CBD=45°，
∵EG⊥AB，EH⊥BC，∠ABC=90°，
∴GE=EH，∠GEH=90°，
∴∠CEF=∠GEH，
∴∠CEH=∠GEF，
在△ECH和△EFG中，
∠CEH=∠GEFEH=EC∠EHC=∠EGF=90°，
∴△ECH≌△EFG(ASA)，
∴CE=EF；
(2)证明：如图，过点E作EH⊥BC于H，交AD于Q，EG⊥AB于G，交CD于P，

∵CE=EF，CE⊥EF，
∴△CEF是等腰直角三角形，
∴CF=2CE，
∵PG⊥AB，QH⊥AD，∠A=∠ADC=∠DCB=∠ABC=90°，
∴四边形AGPD是矩形，四边形DQHC是矩形，四边形DQEP是矩形，
∴DQ=CH，DP=AG，
∵∠ADB=∠CDB=45°，EQ⊥AD，EP⊥CD，
∴EP=EQ，
∴四边形DPEQ是正方形，
∴DQ=DP=PE=QE=CH=AG，
∵△ECH≌△EFG，
∴GF=CH=DQ，
∵ME⊥BD，∠ADB=45°，
∴△DEM是等腰直角三角形，
∵EQ⊥AD，
∴DQ=QM，
∴DQ=QM=GF=AG，
∴DM=AF，
∵AD=AB，
∴DM=BF，
又∵AB=BC，∠A=∠CBF=90°，
∴△ABM≌△BCF(SAS)，
∴BM=CF，
∴BM=2CE；
(3)解：如图，过点E作GE⊥AB于G，EQ⊥AD于Q，

由(2)可知：AG=GF=QE，
∵EG⊥AB，∠ABD=45°，
∴△EGB是等腰直角三角形，
∵BE=72，
∴BG=EG=7，
∵EQ⊥AD，EG⊥AB，∠A=90°，
∴四边形AGEQ是矩形，
∴AQ=EG=7，
∴QN=1，
∵NF2=EN2+EF2=AN2+AF2，EN2=QE2+QN2，EF2=EG2+GF2，
∴36+4GF2=GF2+1+49+GF2，
∴GF2=7，
∴EF2=49+7=56，
∴EF=214=CE，
故答案为：214．
(1)由“ASA”可证△ECH≌△EFG，可得CE=EF；
(2)由正方形的性质和矩形的性质可证DQ=QM=GF=AG，由“SAS”可证△ABM≌△BCF，可得BM=CF，可得结论；
(3)由勾股定理列出方程可求EF的长．
本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题
28.【答案】解：(1)y=kx−k+3=k(x−1)+3，
当x=1时，y=3，
即点P的坐标为(1,3)；
(2))点B在直线y=kx−k+3上，当x=2时，y=k+3，即点B(2,k+3,)，
设直线y=kx−k+3与y轴交于点H，令x=0，则y=−k+3，即点H(0,−k+3,)，如图1，
，
∵BP平分∠OBA，
∴∠ABH=∠OBH，
∵AB//y，
∴∠ABH=∠OHB，
∴∠OBH=∠OHB，
则OB=OH，
即22+(k+3)2=(3−k)2，
解得：k=−33；
(3)△PQR中，∠QPR=120°，PQ=PR，过点P作PE⊥QR，
∴∠Q=30°，PE=12PQ，QE=ER=QP2−PE2=QP2−(12QP)2=32QP，QR=2QE=3QP，

∴3OR+QR=3OR+3QP=3(OR+QP)，
∴当OR+QP的值最小时，3OR+QR的值就是最小值，
如图：x轴以点P为旋转中心，逆时针旋转120°，点O旋转到点M位置，点Q与点R重合，△OPQ≌△MPR，

∴∠QCO=60°，
∴tan∠QCO=tan60°=3，
∴设直线RM的解析式为：y=−3x+b，
∵P(1,3)，
∴OP=2=PM，∠POQ=∠PMR=60°=∠QCO，
∴PM//x轴，M(3,3)代入y=−3x+b，得b=43，
∴直线RM的解析式为：y=−3x+43，
∵点O、P是定点，
∴点R在直线RM上运动，
作点P关于直线RM的对称点P′，
∴PR=P′R，
又∵PQ=PR，
∴OR+PR=OP′时，即OR+QP=OP′，此时OR+QP的值最小，
∵P(1,3)，
∴点P关于直线y=−3x+43的对称点P′的坐标为(4,23)，
∴OP′=42+(23)2=27，
∴3OR+QR=3(OR+QP)=3×27=221，
∴3OR+QR的最小值为221．
【解析】(1)y=kx−k+3=k(x−1)+3，当x=1时，y=3，即可求解；
(2)设直线BP交y轴于点H，证明∠OBH=∠OHB，则OB=OH，即可求解；
(3)先根据三线合一得到QR=2QE=3QP，所以3OR+QR=3OR+3QP=3(OR+QP)，把x轴以点P为旋转中心，逆时针旋转120°，点O旋转到点M位置，点Q与点R重合，△OPQ≌△MPR，再解出直线RM的解析式，得点P关于此直线的对称点P′坐标，再根据OR+PR=OP′时，即OR+QP=OP′，此时OR+QP的值最小即可解答．
本题综合考查了一次函数与几何知识的应用，难度较大，解题关键是找到点R的运动轨迹，问题转化到最短路劲问题或者将军饮马问题，属于中考重点考查知识点．
成绩/m
1.50
1.60
1.70
1.80
人数/个
2
3
4
1
甲型客车
乙型客车
载客量/(人/辆)
45
30
租金/(元/辆)
400
280