
2021-2022学年陕西省西安市长安区七年级(下)期末数学试卷(含解析)
展开一、选择题(本大题共10小题,共30分)
下列交通标志图案是轴对称图形的是( )
A. B. C. D.
如图,点A,D,B,F在一条直线上,△ABC≌△FDE.若AF=10,AD=3.5,则BD的长为( )
A. 3
B. 3.5
C. 6
D. 7
若气象部门预报明天下雨的概率是70%,下列说法正确的是( )
A. 明天下雨的可能性比较大B. 明天下雨的可能性比较小
C. 明天一定会下雨D. 明天一定不会下雨
若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )
A. 1B. 2C. 4D. 8
下列计算正确的是( )
A. (a+b)2=a2+b2B. 2a3⋅3a2=6a6
C. 2a+3b=5abD. (−a3)4=a12
如图,已知∠1=∠2,要得到△ABD≌△ACD,还需要从下列条件中补选一个,补上仍不能判断其全等的是( )
A. ∠BAD=∠CAD
B. ∠B=∠C
C. BD=CD
D. AB=AC
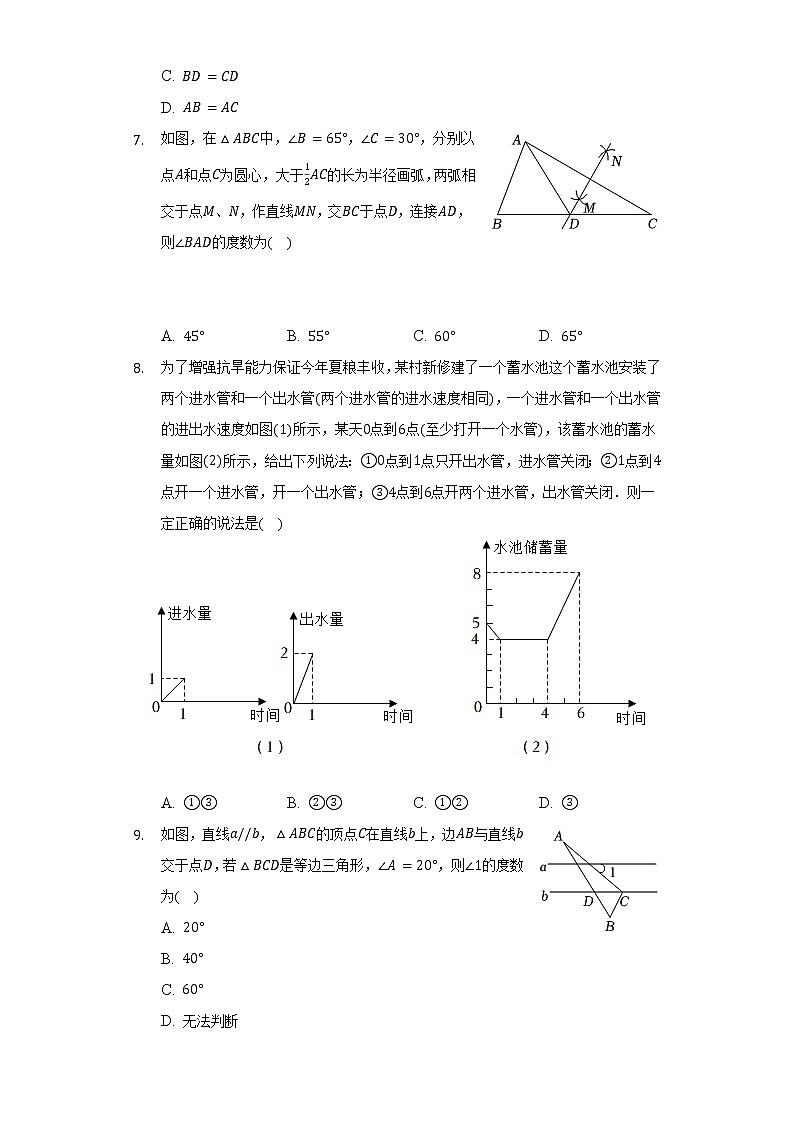
如图,在△ABC中,∠B=65°,∠C=30°,分别以点A和点C为圆心,大于12AC的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
A. 45°B. 55°C. 60°D. 65°
为了增强抗旱能力保证今年夏粮丰收,某村新修建了一个蓄水池这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同),一个进水管和一个出水管的进出水速度如图(1)所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图(2)所示,给出下列说法:①0点到1点只开出水管,进水管关闭;②1点到4点开一个进水管,开一个出水管;③4点到6点开两个进水管,出水管关闭.则一定正确的说法是( )
A. ①③B. ②③C. ①②D. ③
如图,直线a//b,△ABC的顶点C在直线b上,边AB与直线b交于点D,若△BCD是等边三角形,∠A=20°,则∠1的度数为( )
A. 20°
B. 40°
C. 60°
D. 无法判断
如图,在△ABC中,点D在BA的延长线上,点E在BC边上,连接DE交AC于点F,已知∠DFC=3∠B=123°,∠C=∠D,则∠BED的度数为( )
A. 102°B. 98°C. 88°D. 82°
二、填空题(本大题共8小题,共24分)
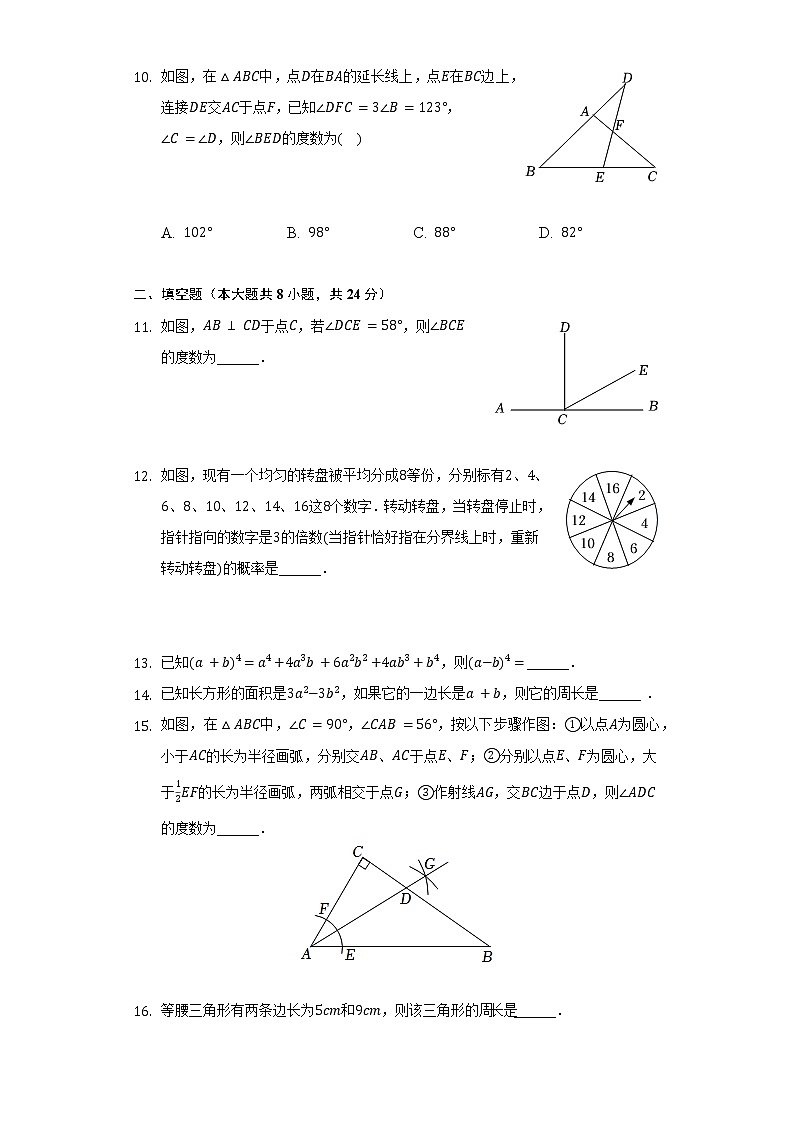
如图,AB⊥CD于点C,若∠DCE=58°,则∠BCE的度数为______.
如图,现有一个均匀的转盘被平均分成8等份,分别标有2、4、6、8、10、12、14、16这8个数字.转动转盘,当转盘停止时,指针指向的数字是3的倍数(当指针恰好指在分界线上时,重新转动转盘)的概率是______.
已知(a+b)4=a4+4a3b+6a2b2+4ab3+b4,则(a−b)4=______.
已知长方形的面积是3a2−3b2,如果它的一边长是a+b,则它的周长是______ .
如图,在△ABC中,∠C=90°,∠CAB=56°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于12EF的长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为______.
等腰三角形有两条边长为5cm和9cm,则该三角形的周长是______.
如图,甲、乙、丙3人站在5×6网格中的三个格子中,小王随机站在剩下的空格中,与图中3人均不在同一行的概率是______.
在等腰△ABC中,AB=AC,AC腰上的中线BD将△ABC的周长分为15和27两部分,则这个三角形的底边长为______.
三、解答题(本大题共6小题,共46分)
计算:
(1)−42⋅(−12)3−(−1)2022;
(2)[(3xy+1)(3xy−1)+(xy−1)2]÷2xy.
如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,试说明:点O是AC的中点.请你在横线上补充其推理过程或理由.
解:因为BF=DE
所以BF−EF=DE−EF,即______,
因为AB=CD,AE=CF,
所以______(理由:SSS).
所以∠B=∠D(理由:______).
因为∠AOB=∠COD(理由:______),
所以△ABO≌△CDO(理由:______).
所以______(理由:全等三角形对应边相等).
所以点O是AC的中点.
尺规作图(保留作图痕迹,不写作法)
(1)如图1,已知∠AOB,作出∠AOB的对称轴a;
(2)如图2,已知四边形ABCD,AD//BC,∠B=∠C,作出四边形ABCD的对称轴b.
一个不透明的口袋中装有6个红球,9个黄球,3个白球,这些球除颜色外其他均相同.从中任意摸出一个球.
(1)求摸到的球是白球的概率.
(2)如果要使摸到白球的概率为14,需要在这个口袋中再放入多少个白球?
如图在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)试说明:△ABE≌△DBE;
(2)若∠A=105°,∠C=50°,求∠DEC的度数.
甲、乙两位同学从A地出发在同一条路上骑自行车到B地,他们离出发地的距离S(千米)与甲行驶时间t(小时)之间的函数关系图象如图所示,根据图中提供的信息解答下列问题:
(1)A地到B地的距离多少千米?甲中途停留了多长时间?
(2)求乙骑行的速度多少?
(3)求甲在停留时离A地的距离是多少千米?
(4)求甲在停留后,他离出发地的距离S和t之间的函数关系式;
(5)求乙到达B地时,甲离B地的距离是多少?
答案和解析
1.【答案】A
【解析】解:A、是轴对称图形,故此选项符合题意;
B、不是轴对称图形,故此选项不合题意;
C、不是轴对称图形,故此选项不合题意;
D、不是轴对称图形,故此选项不合题意.
故选:A.
根据轴对称图形的概念求解.
本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
2.【答案】A
【解析】解:∵△ABC≌△FDE,
∴AB=DF,
∴AB−BD=DF−BD,
即AD=BF,
∵AD=3.5,
∴BF=3.5,
∵AF=10,
∴BD=AF−AD−BF=10−3.5−3.5=3,
故选:A.
根据全等三角形的性质得出AB=DF,求出AD=BF=3.5,再代入BD=AF−AD−BF求出即可.
本题考查了全等三角形的性质,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应角相等,对应边相等.
3.【答案】A
【解析】解:“明天下雨的概率是70%”说明明天下雨的可能性比较大,在70%左右,因此选项A符合题意;
明天下雨的可能性超过了一半,不能说下雨的可能性比较小,因此选项B不符合题意;
“明天下雨的概率是70%”并不能说明明天一定会下雨或明天一定不会下雨,因此选项C、选项D不符合题意;
故选:A.
根据概率的意义逐项进行判断即可.
本题考查概率的意义,理解概率的意义是正确判断的前提.
4.【答案】C
【解析】解:由三角形三边关系定理得:5−3
故选:C.
根据三角形三边关系定理得出5−3
【解析】解:A、原式=a2+2ab+b2,不符合题意;
B、原式=6a5,不符合题意;
C、原式不能合并,不符合题意;
D、原式=a12,符合题意.
故选:D.
各式计算得到结果,即可作出判断.
此题考查了完全平方公式,合并同类项,幂的乘方与积的乘方,以及单项式乘单项式,熟练掌握运算法则及公式是解本题的关键.
6.【答案】D
【解析】解:∵∠1+∠ADB=180°,∠2+∠ADC=180°,∠1=∠2,
∴∠ADB=∠ADC,
A、∵∠BAD=∠CAD,AD=AD,∠ADB=∠ADC,
∴△ABD≌△ACD(ASA),
故A不符合题意;
B、∵∠B=∠C,AD=AD,∠ADB=∠ADC,
∴△ABD≌△ACD(AAS),
故B不符合题意;
C、∵BD=DC,AD=AD,∠ADB=∠ADC,
∴△ABD≌△ACD(SAS),
故C不符合题意;
D、∵AB=AC,AD=AD,∠ADB=∠ADC,
∴△ABD与△ACD不一定全等,
故D符合题意;
故选:D.
根据等角的补角相等可得∠ADB=∠ADC,然后根据全等三角形的判定方法:SAS,ASA,AAS,SSS,逐一判断即可解答.
本题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.
7.【答案】B
【解析】解:在△ABC中,
∵∠B=65°,∠C=30°,
∴∠BAC=180°−∠B−∠C=85°,
由作图可知MN为AC的中垂线,
∴DA=DC,
∴∠DAC=∠C=30°,
∴∠BAD=∠BAC−∠DAC=55°,
故选:B.
根据内角和定理求得∠BAC=85°,由中垂线性质知DA=DC,即∠DAC=∠C=30°,从而得出答案.
本题主要考查作图−基本作图,熟练掌握中垂线的作图和性质是解题的关键.
8.【答案】D
【解析】解:由题意可得:
①0点到1点既进水,也出水;
②1点到4点同时打开两个管进水,和一只管出水;
③4点到6点只进水,不出水.
正确的只有③.
故选:D.
根据图象1可知进水速度小于出水速度,结合图2中特殊点的实际意义即可作出判断.
本题主要考查了函数图象的读图能力和函数与实际问题结合的应用.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
9.【答案】B
【解析】解:∵△BCD是等边三角形,
∴∠B=∠BCD=60°,
∵∠A=20°,
∴∠ACB=180°−∠A−∠B=180°−20°−60°=100°,
∴∠ACD=∠ACB−∠BCD=100°−60°=40°,
∵a//b,
∴∠1=∠ACD=40°,
故选:B.
根据等边三角形的性质得出∠B=∠BCD=60°,根据三角形内角和定理求出∠ACB,求出∠ACD,再根据平行线的性质求出即可.
本题考查了平行线的性质,等边三角形的性质等知识点,能熟记等边三角形的性质是解此题的关键.
10.【答案】B
【解析】解:∵∠DFC=3∠B=123°,
∴∠B=41°,
设∠C=∠D=x°,
则41+x+x=123,
解得:x=41,
∴∠D=41°,
∴∠BED=180°−41°−41°=98°.
故选:B.
首先根据∠DFC=3∠B=123°,求出∠B=41°,然后设∠C=∠D=x°,根据外角与内角的关系,可得:41+x+x=123,据此求出x=41,最后根据三角形内角和定理,求出∠BED的度数即可.
此题主要考查了三角形的内角和定理,解答此题的关键是要明确:(1)三角形的内角和是180°.(2)三角形的一个外角等于和它不相邻的两个内角的和.
11.【答案】32°
【解析】解:∵AB⊥CD,
∴∠DCB=90°,
∵∠BCE+∠DCE=90°,
∴∠BCE=∠DCB−∠DCE=90°−58°=32°.
故答案为:32°.
应用垂线的性质进行计算即可得出答案.
本题主要考查了垂线的性质,熟练掌握垂线的性质进行求解是解决本题的关键.
12.【答案】14
【解析】解:转动转盘,当转盘停止时,指针指向的数字是3的倍数有6和12两种情况,
∴指针指向的数字是3的倍数(当指针恰好指在分界线上时,重新转动转盘)的概率=28=14,
故答案为:14.
直接利用概率公式计算即可.
本题考查了概率的知识.用到的知识点为:概率=所求情况数与总情况数之比.
13.【答案】a4−4a3b+6a2b2−4ab3+b4
【解析】解:根据题意得:(a−b)4=a4−4a3b+6a2b2−4ab3+b4.
故答案为:(a−b)4=a4−4a3b+6a2b2−4ab3+b4.
把已知等式中的b换为−b,即可即可得到结果.
此题考查了完全平方公式,弄清题意是解本题的关键.
14.【答案】8a−4b
【解析】解:(3a2−3b2)÷(a+b)
=3(a+b)(a−b)÷(a+b)
=3a−3b.所以另一边长为3a−3b
∴可得周长为:2[(a+b)+(3a−3b)]=8a−4b.
故应填:8a−4b.
根据长方形的面积和已知边长,利用多项式的除法先求出另一边,再根据周长公式列式求解.
本题考查的是整式的除法和加减法的应用,首先应根据所给条件运用整式除法进行计算,然后进行整式的加减计算.注意合并同类项的法则的应用,要将其与整式乘法法则区别开来.
15.【答案】62°
【解析】解:由作图可知AD平分∠CAB,
∴∠CAD=12∠CAB=28°,
∵∠C=90°,
∴∠ADC=90°−28°=62°,
故答案为:62°.
利用角平分线的定义求出∠CAD,可得结论.
本题考查作图−复杂作图,角平分线的定义,解题的关键是掌握角平分线的定义,属于中考常考题型.
16.【答案】19cm或23cm
【解析】解:当等腰三角形的腰长为5cm,底边长为9cm时,
∵5+5>9,9−5<5,
∴能够成三角形,
∴三角形的周长=5+5+9=19(cm);
当等腰三角形的腰长为9cm,底边长为5cm时,
∵9+5>9,9−5<5,
∴能够成三角形,
∴三角形的周长=9+9+5=23(cm).
∴该三角形的周长是19cm或23cm.
故答案为:19cm或23cm.
由于等腰三角形的腰和底边的长不能确定,故应分两种情况进行讨论.
本题考查的是等腰三角形的性质及三角形的三边关系,解答此题时要注意分类讨论,不要漏解.
17.【答案】59
【解析】解:甲、乙、丙3人站在5×6网格中的三个格子中,空格有:5×6−3=27(个),
则小王随机站在剩下的空格中,与图中3人均不在同一行的结果有15个,
∴小王随机站在剩下的空格中,与图中3人均不在同一行的概率为1527=59,
故答案为:59.
由题意得空格有5×6−3=27(个),则小王随机站在剩下的空格中,与图中3人均不在同一行的结果有15个,再由概率公式求解即可.
本题考查了概率公式,由题意得出与图中3人均不在同一行的个数是解题的关键.
18.【答案】6
【解析】解:∵BD是等腰△ABC的中线,可设AD=CD=x,则AB=AC=2x,
又知BD将三角形周长分为15和21两部分,
∴可知分为两种情况:
①AB+AD=15,即3x=15,解得x=5,此时BC=27−x=27−5=22,此时等腰△ABC的三边分别为10,10,22;
②AB+AD=27,即3x=27,解得x=9;此时等腰△ABC的三边分别为18,18,6.
经验证,第一种情况不成立,
∴这个三角形的底边长为6.
故答案为:6.
本题由题意可知有两种情况,AB+AD=15或AB+AD=27.从而根据等腰三角形的性质及三角形三边关系可求出底边为6.
本题主要考查等腰三角形的性质及三角形三边关系;注意:求出的结果一定要检验时符合三角形三边性质.分类讨论是正确解答本题的关键.
19.【答案】解:(1)−42⋅(−12)3−(−1)2022
=−16×(−18)−1
=2−1
=1;
(2)[(3xy+1)(3xy−1)+(xy−1)2]÷2xy
=(9x2y2−1+x2y2−2xy+1)÷2xy
=(10x2y2−2xy)÷2xy
=5xy−1.
【解析】(1)先算乘方,再算乘法,后算减法,即可解答;
(2)先利用平方差公式,完全平方公式算括号里,再算括号外,即可解答.
本题考查了整式的混合运算,准确熟练地进行计算是解题的关键.
20.【答案】BE=DF △ABE≌△CDF 全等三角形对应角相等 对顶角相等 AAS AO=CO
【解析】解:因为BF=DE,
所以BF−EF=DE−EF,即BE=DF,
因为AB=CD,AE=CF,
所以△ABE≌△CDF(理由:SSS).
所以∠B=∠D(理由:全等三角形对应角相等).
因为∠AOB=∠COD(理由:对顶角相等),
所以△ABO≌△CDO(理由:AAS).
所以AO=CO(理由:全等三角形对应边相等).
所以点O是AC的中点.
故答案为:BE=DF,△ABE≌△CDF,全等三角形对应角相等,对顶角相等,AAS,AO=CO.
由“SSS”可证△ABE≌△CDF,可得∠B=∠D,由“AAS”可证△ABO≌△CDO,可得AO=CO,即可求解.
本题考查了全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键.
21.【答案】解:(1)作∠AOB的平分线,如图.
(2)∵AD//BC,∠B=∠C,
∴四边形ABCD为等腰梯形,
作线段BC的垂直平分线,即为四边形ABCD的对称轴b,如图.
【解析】(1)作出∠AOB的平分线即可.
(2)作出线段BC的垂直平分线即可.
本题考查轴对称的性质,熟练掌握角平分线及线段的垂直平分线的作法是解答本题的关键.
22.【答案】解:(1)根据题意分析可得:口袋中装有红球6个,黄球9个,白球3个,共18个球,
故P(摸到白球)=318=16;
(2)设需要在这个口袋中再放入x个白球,得:3+x18+x=14,
解得:x=2.
所以需要在这个口袋中再放入2个白球.
【解析】(1)直接利用概率公式求解即可;
(2)根据绿球的概率公式得到相应的方程,求解即可.
本题考查概率的求法与运用,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=mn.
23.【答案】(1)证明:∵BE平分∠ABC,
∴∠ABE=∠DBE,
在△ABE和△DBE中,
AB=DB∠ABE=∠DBEBE=BE,
∴△ABE≌△DBE(SAS);
(2)解:∵∠A=105°,∠C=50°,△ABE≌△DBE,
∴∠BDE=∠A=105°,
∴∠EDC=180°−∠BDE=180°−105°=75°,
∴∠DEC=180°−∠EDC−∠C=180°−75°−50°=55°.
【解析】(1)根据BE平分∠ABC,可以得到∠ABE=∠DBE,然后根据题目中的条件即可证明△ABE和△DBE全等,从而可以得到结论成立;
(2)根据全等三角形的性质及三角形内角和定理可求出∠DEC的度数.
本题考查全等三角形的判定与性质、角平分线的性质,解答本题的关键是明确题意,利用全等三角形的判定和性质解答.
24.【答案】解:(1)由图象可知,A地到B地的距离是18千米,甲中途停留了1−0.5=0.5(小时);
(2)乙骑行的速度是18÷(2−0.5)=12(千米/小时);
(3)甲在停留时离A地的距离即是乙0.5小时所行路程,
∴甲在停留时离A地的距离是12×0.5=6(千米);
(4)设甲在停留后,他离出发地的距离S和t之间的函数关系式为S=kt+b,将(1,6),(2.5,18)代入得:
k+b=62.5k+b=18,
解得k=8b=−2,
∴甲在停留后,他离出发地的距离S和t之间的函数关系式为S=8t−2;
(5)在S=8t−2中,令t=2得S=8×2−2=14,
∴乙到达B地时,甲离B地的距离是18−14=4(千米).
【解析】(1)由图象可直接得答案;
(2)由速度=路程÷时间可得乙骑行的速度;
(3)求出乙0.5小时所走路程即是甲在停留时离A地的距离;
(4)用待定系数法可得答案;
(5)结合(4),算出S的值,即可求出乙到达B地时,甲离B地的距离.
本题考查一次函数的应用,解题的关键是读懂题意,能正确识图.
题号
一
二
三
总分
得分
2023-2024学年陕西省西安市长安区七年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年陕西省西安市长安区七年级(下)期末数学试卷(含详细答案解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年陕西省西安市长安区八年级(下)期末数学试卷(含解析): 这是一份2023-2024学年陕西省西安市长安区八年级(下)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年陕西省西安市长安区七年级(下)期末数学试卷(含解析): 这是一份2023-2024学年陕西省西安市长安区七年级(下)期末数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












