【2023届必备】2023版高考一轮复习训练5　函数的性质

这是一份【2023届必备】2023版高考一轮复习训练5　函数的性质，共5页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
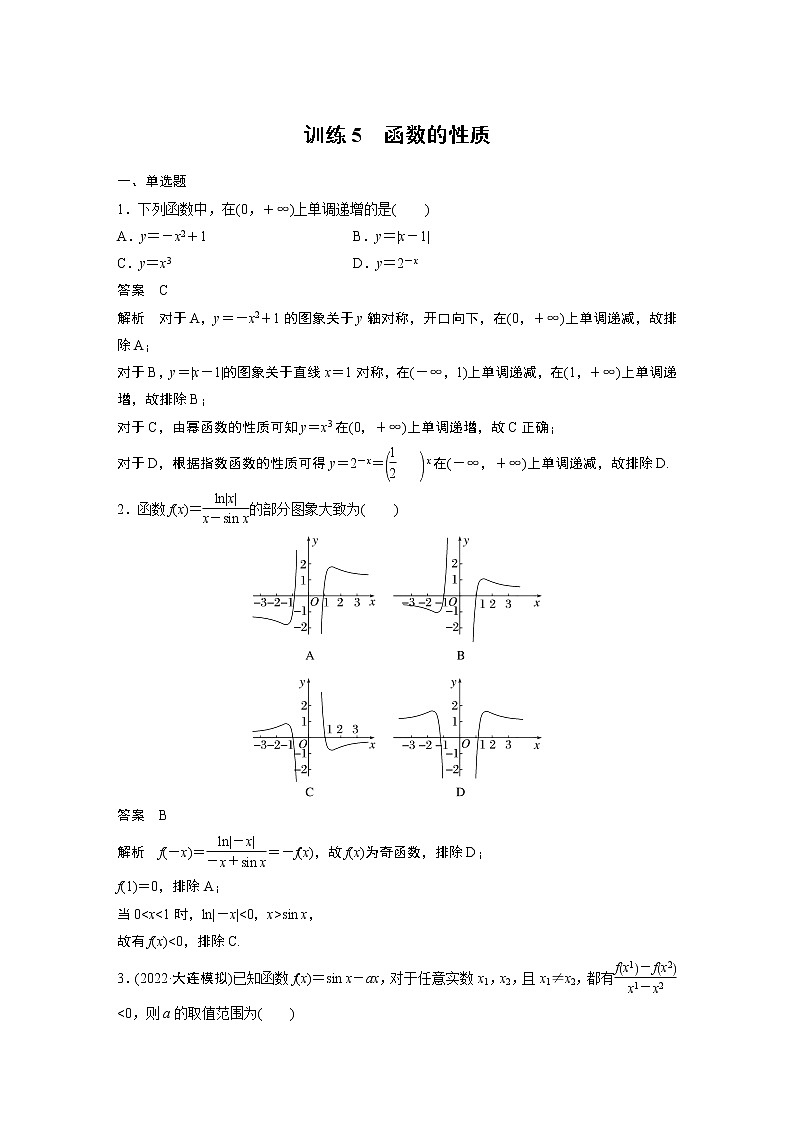
训练5　函数的性质一、单选题1．下列函数中，在(0，＋∞)上单调递增的是(　　)A．y＝－x2＋1   B．y＝|x－1|C．y＝x3   D．y＝2－x答案　C解析　对于A，y＝－x2＋1的图象关于y轴对称，开口向下，在(0，＋∞)上单调递减，故排除A；对于B，y＝|x－1|的图象关于直线x＝1对称，在(－∞，1)上单调递减，在(1，＋∞)上单调递增，故排除B；对于C，由幂函数的性质可知y＝x3在(0，＋∞)上单调递增，故C正确；对于D，根据指数函数的性质可得y＝2－x＝x在(－∞，＋∞)上单调递减，故排除D.2．函数f(x)＝的部分图象大致为(　　)答案　B解析　f(－x)＝＝－f(x)，故f(x)为奇函数，排除D；f(1)＝0，排除A；当0<x<1时，ln|－x|<0，x>sin x，故有f(x)<0，排除C.3．(2022·大连模拟)已知函数f(x)＝sin x－ax，对于任意实数x1，x2，且x1≠x2，都有<0，则a的取值范围为(　　)A．a≤－1   B．a>1C．a<－1   D．a≥1答案　D解析　由题意知，f(x)在定义域内单调递减，∴f′(x)＝cos x－a≤0在x∈R上恒成立，即cos x≤a在x∈R上恒成立，∴a≥1.4．(2022·南京模拟)已知函数f(x)＝ln ，则(　　)A．f(x)的图象关于点(2,0)对称B．f(x)的图象关于直线x＝2对称C．f(x)在(0,4)上单调递减D．f(x)在(0,2)上单调递减，在(2,4)上单调递增答案　A解析　由题意，函数f(x)＝ln ，可得>0，解得0<x<4，令t＝＝－1－，故t＝在(0,4)上单调递增，所以函数f(x)＝ln 在(0,4)上单调递增，可排除B，C，D；又由f(x)＝ln ，满足f(4－x)＝－f(x)，所以函数f(x)＝ln 的图象关于点(2,0)对称．二、多选题5．函数f(x)为定义在R上的偶函数，且满足f(2＋x)＝f(2－x)，若当x∈[0,2]时，f(x)＝3x＋2x－1，则下列结论正确的是(　　)A．f(x)的周期为4B．f(x)在[－4，－2]上单调递减C．f(x)关于直线x＝－2对称D．f(2 022)＝12答案　ACD解析　由f(x)＝f(－x)，f(2＋x)＝f(2－x)⇒f(x＋2)＝f(x－2)，所以f(x＋4)＝f(x＋2－2)＝f(x)，即f(x＋4)＝f(x)，故函数f(x)是周期为4的周期函数，选项A正确；当x∈[0,2]时，f(x)＝3x＋2x－1，则f(x)在[0,2]上单调递增，所以f(x)在[－4，－2]上单调递增，故选项B错误；因为f(x)为周期为4的偶函数，所以f(x)的图象关于直线x＝－2对称，故选项C正确；因为函数f(x)是周期为4的偶函数，则f(2 022)＝f(505×4＋2)＝f(2)＝9＋4－1＝12，故选项D正确．6．(2022·永州模拟)已知函数f(x)是奇函数，f(x＋1)是偶函数，并且当x∈(0,1)时，f(x)＝2|x－2|－3，则下列选项正确的是(　　)A．f(x)在(－3，－2)上为减函数B．f(x)在上恒小于0C．f(x)在[1,2]上为增函数D．f(x)关于x＝3对称答案　BD解析　因为f(x)是奇函数，f(x＋1)是偶函数，所以函数f(x)的图象关于(0,0)中心对称，且关于x＝1轴对称，则f(x)的周期为4，当x∈(0,1)时，f(x)＝2|x－2|－3＝1－2x，则函数f(x)在x∈(0,1)上单调递减，根据对称性可得f(x)在x∈(1,2)上单调递增，再结合周期性可得f(x)在(－3，－2)上为增函数，故A错误；当x∈时，f(x)<0，根据对称性可得当x∈时，f(x)<0，故B正确；f(x)的图象关于x＝1轴对称，所以f ＝f ＝0，f(2)＝f(0)＝0，所以f(x)在[1,2]上不可能为增函数，故C错误；f(x)的图象关于x＝1轴对称，又f(x)是奇函数，所以f(x)的图象关于x＝－1轴对称，因为f(x)的周期为4，所以f(x)关于x＝3对称，故D正确．三、填空题7．写出一个最小值为2 023的偶函数f(x)＝__________________.答案　|x|＋2 023(答案不唯一)解析　若f(x)＝|x|＋2 023，则f(－x)＝|－x|＋2 023＝f(x)，所以f(x)为偶函数，显然f(x)的最小值为2 023，故可以为f(x)＝|x|＋2 023.8．(2022·苏州模拟)设f(x)是定义在(－∞，0)∪(0，＋∞)上的奇函数，对任意的x1，x2∈(0，＋∞)，x1≠x2，满足>0，若f(2)＝4，则不等式f(x)－>0的解集为______________．答案　(－2,0)∪(2，＋∞)解析　令F(x)＝xf(x)，由f(x)是定义在(－∞，0)∪(0，＋∞)上的奇函数，可得F(x)是定义在(－∞，0)∪(0，＋∞)上的偶函数，由对任意的x1，x2∈(0，＋∞)，x1≠x2，满足>0，可得F(x)＝xf(x)在(0，＋∞)上单调递增，由f(2)＝4，可得F(2)＝8，所以F(x)在(－∞，0)上单调递减，且F(－2)＝8，不等式f(x)－>0，即为>0，即>0，可得或即或解得x>2或－2<x<0.四、解答题9．设函数f(x)是定义在R上的奇函数，对任意实数x有f ＝－f 成立．(1)证明y＝f(x)是周期函数，并指出其周期；(2)若f(1)＝2，求f(2)＋f(3)的值．(1)证明　由f ＝－f ，且f(－x)＝－f(x)，知f(3＋x)＝f ＝－f ＝－f(－x)＝f(x)，所以y＝f(x)是周期函数，且T＝3是其一个周期．(2)因为f(x)为定义在R上的奇函数，所以f(0)＝0，且f(－1)＝－f(1)＝－2，又T＝3是y＝f(x)的一个周期，所以f(2)＋f(3)＝f(－1)＋f(0)＝－2＋0＝－2.10．(2022·山东师大附中模拟)函数f(x)＝为R上的奇函数，若f(x)＝k在(－∞，0)上有解，求实数k的取值范围．解　由题意，函数f(x)＝为R上的奇函数，令x＝0，得f(0)＝＝0，即m＋m－2＝0，解得m＝1，即f(x)＝，又由k＝f(x)＝＝＝1－，因为x∈(－∞，0)，所以1<2x＋1<2，所以1>>，可得－1<f(x)<0，所以k∈(－1,0)，即实数k的取值范围是(－1,0)．