人教A版 (2019)必修 第一册5.6 函数 y=Asin（ ωx ＋ φ）课时作业

5.6　函数y=Asin(ωx+φ)

5.6.1　匀速圆周运动的数学模型

5.6.2　函数y=Asin(ωx+φ)的图象

基础过关练

题组一　三角函数的图象及图象变换

1.(2020广东湛江期末)将函数y=sin的图象向右平移个单位长度后,得到的图象对应的函数解析式为(　　)

A.y=sin　　　　　　B.y=-sin

C.y=cos 2x　　　　　　D.y=-cos 2x

2.(多选)(2022重庆巴蜀中学期末)要得到函数y=3cos x的图象,只需将y=3cos的图象上所有的点(　　)

A.横坐标伸长到原来的2倍,再向左平移个单位长度

B.横坐标伸长到原来的2倍,再向左平移个单位长度

C.向左平移个单位长度,再把横坐标伸长到原来的2倍

D.向左平移个单位长度,再把横坐标缩短到原来的

3.(2022安徽合肥期末)将函数f(x)=2sin(2x+φ)(0<φ<π)的图象向左平移个单位长度后,所得函数图象关于原点对称,则f=(　　)

A.-2　　　　　B.-1　　　　　C.1　　　　　D.2

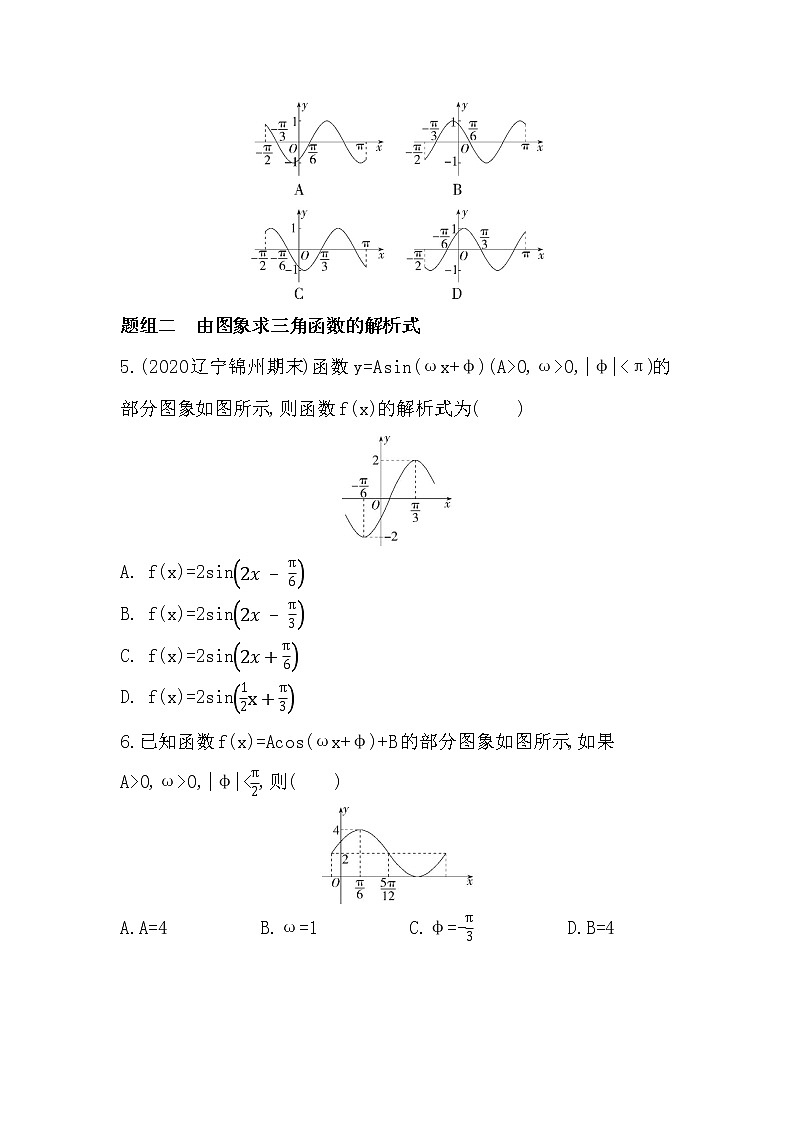
4.(2022广东肇庆期末)函数y=f(x)=sin在区间上的简图是(　　)

题组二　由图象求三角函数的解析式

5.(2020辽宁锦州期末)函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为(　　)

A. f(x)=2sin

B. f(x)=2sin

C. f(x)=2sin

D. f(x)=2sin

6.已知函数f(x)=Acos(ωx+φ)+B的部分图象如图所示,如果A>0,ω>0,|φ|<,则(　　)

A.A=4　　　　　B.ω=1　　　　　C.φ=-　　　　　D.B=4

7.(2020山东聊城期末质量检测)用五点法作函数y=Asin(ωx+φ)的图象时,得到如下表格:

则A,ω,φ的值分别为(　　)

A.4,2,-　　　　　　B.4,,

C.4,2,　　　　　　D.4,,-

8.已知函数f(x)=Acos(ωx+φ)(其中A>0,ω>0)的部分图象如图所示, f=-,则f(0)=(　　)

A.-　　　　　B.-　　　　　C.　　　　　D.

题组三　三角函数图象与性质的综合应用

9.(多选)已知函数f(x)=Acos(ωx+φ)A>0,ω>0,|φ|<的部分图象如图所示,要得到f(x)的图象,只需将y=2cos x的图象上所有的点(　　)

A.横坐标变为原来的,再向右平移个单位长度

B.横坐标变为原来的2倍,再向左平移个单位长度

C.向右平移个单位长度,再把横坐标变为原来的

D.向左平移个单位长度,再把横坐标变为原来的2倍

10.(2022湖南常德期末)已知函数f(x)=Asin(ωx+φ)的部分图象如图所示,则下列结论中正确的是(　　)

A.若x∈,则函数f(x)的值域为

B.点是函数f(x)的图象的对称中心

C.函数f(x)在区间上是增函数

D.函数f(x)的图象可以由函数y=cos 2x的图象向右平移个单位长度得到

11.已知f(x)=2sin.

(1)用“五点法”作出函数f(x)在一个周期内的图象;

(2)写出f(x)的单调递增区间;

(3)求f(x)的最大值和此时x的取值集合.

12.已知函数f(x)=Asin(ωx+φ)A>0,ω>0,|φ|<的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).

(1)求f(x)的解析式及x0的值;

(2)求f(x)的单调递增区间.

13.函数f(x)=Asin(ωx+φ)的部分图象如图所示.

(1)求函数f(x)的解析式;

(2)将函数f(x)的图象向右平移个单位长度,得到g(x)的图象.求直线y=与函数y=f(x)+g(x)的图象在内所有交点的横坐标之和.

能力提升练

题组一　三角函数图象的变换

1.(2022江苏南京师范大学附属中学期末)将函数f(x)的图象向左平移个单位长度,再将所得图象上各点的横坐标变为原来的,纵坐标不变,得到函数g(x)的图象.已知g(x)=sin,则f(x)=(　　)

A.-sin 4x　　　　　　B.sin x

C.sin　　　　　　D.sin

2.(2022安徽蚌埠期末)将函数f(x)=sin 2x+2cos2x-1的图象向右平移个单位长度后得到函数g(x)的图象,则函数g(x)=(　　)

A.2sin　　　　　　B.2sin

C.2cos　　　　　　D.2cos

3.(2020河南郑州期末)若点A在函数f(x)=cos(2x+φ)的图象上,为了得到函数y=sin的图象,只需把曲线f(x)上所有的点(　　)

A.向左平移个单位长度

B.向右平移个单位长度

C.向右平移个单位长度

D.向左平移个单位长度

4.(2022广东东莞期末)若将函数f(x)=sin的图象向右平移φ(φ>0)个单位长度,得到的函数图象关于y轴对称,则φ的最小值为(　　)

A.　　　　　B.　　　　　C.　　　　　D.

题组二　函数y=Asin(ωx+φ)图象的应用

5.(多选)(2020山东菏泽期末)已知函数f(x)=sin(ωx+φ)的最小正周期为π,将该函数的图象向左平移个单位长度后,得到的图象对应的函数g(x)为偶函数,则下列说法正确的是(　　)

A. f(0)=

B.函数y=f(x)的图象关于直线x=对称

C.函数y=f(x)的图象关于点对称

D.函数y=f(x)的图象关于直线x=对称

6.(多选)(2022广东深圳高级中学期末)已知函数f(x)=sin,则下列说法正确的是(　　)

A.函数f为偶函数

B. f(π)=-

C.若|f(x1)-f(x2)|=2,则|x1-x2|的最小值为

D.函数f(x)的图象向右平移个单位长度得到函数y=-cos 3x的图象

7.(2021安徽淮南第一中学月考)将函数f(x)=2sin的图象向右平移4t(t>0)个单位长度,再将图象上各点的横坐标缩短到原来的(纵坐标不变),得到函数y=g(x)的图象,若对任意的x∈R均有g(x)≥g成立,则y=g(x)的图象(　　)

A.关于直线x=-对称

B.关于直线x=对称

C.关于点对称

D.关于点对称

8.(2020河南郑州期末)已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,则φ的值为　　　　. 

9.(2022甘肃兰州第二中学期末)已知函数f(x)=Asin(ωx+φ)A>0,ω>0,-<φ<在一个周期内的图象如图所示.

(1)求函数f(x)的最小正周期T及f(x)的解析式;

(2)求函数f(x)的图象的对称轴方程及单调递增区间;

(3)将f(x)的图象向右平移个单位长度,再将所得图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数g(x)的图象,若g(x)=a-1在x∈上有两个不同的解,求a的取值范围.

10.(2020辽宁辽阳期末)已知函数f(x)=Asin(ωx+φ)A>0,ω>0,|φ|<的部分图象如图所示.

(1)求A,ω和φ的值;

(2)求函数y=f(x)在[1,2]上的单调递减区间;

(3)若函数y=f(x)在区间[a,b]上恰有2 020个零点,求b-a的取值范围.

答案全解全析

基础过关练

1.D　将函数y=sin的图象向右平移个单位长度后,得到的图象对应的函数解析式为y=sin=sin=-cos 2x.故选D.

2.AC　将y=3cos的图象上所有点的横坐标伸长到原来的2倍,得到y=3cos的图象,若将所得图象向左平移个单位长度,则得到y=3cos=3cos x的图象;若将所得图象向左平移个单位长度,则得到y=3cos=3cos的图象,故A正确,B错误.

将y=3cos的图象上所有的点向左平移个单位长度,得到y=3cos=3cos 2x的图象,再将所得图象上所有点的横坐标伸长到原来的2倍,得到y=3cos x的图象,故C正确.

将y=3cos的图象上所有的点向左平移个单位长度,得到y=3cos=3cos2x+的图象,再将所得图象上所有点的横坐标缩短到原来的,得到y=3cos的图象,故D错误.故选AC.

3.D　将函数f(x)=2sin(2x+φ)(0<φ<π)的图象向左平移个单位长度后,得到y=2sin=2sin(0<φ<π)的图象,

∵此图象关于原点对称,∴+φ=kπ,k∈Z,即φ=kπ-,k∈Z,又0<φ<π,

∴φ=,∴ f(x)=2sin,

∴f=2sin=2.故选D.

4.C　因为y=f(x)=sin,

所以f(0)=sin=-<0,所以排除B,D;

令2kπ-≤2x+≤2kπ+,k∈Z,得kπ-≤x≤kπ-,k∈Z,

令2kπ+≤2x+≤2kπ+,k∈Z,得kπ-≤x≤kπ+,k∈Z,

所以函数f(x)在上单调递增,在上单调递减,所以排除A.

故选C.

5.A　由题图可得A=2,×=+,

∴ω=2.

由五点画图法,可得2×+φ=,

∴φ=-,故f(x)=2sin,故选A.

6.C　由题中图象可得A==2,B==2,故A,D选项均错误;函数f(x)的最小正周期T=4×=π,∴ω==2,B选项错误;由上述分析可知f(x)=2cos(2x+φ)+2,将点代入函数f(x)的解析式,得2cos+2=4,

∴cos=1,

∵-<φ<,∴-<+φ<,∴φ+=0,

∴φ=-,C选项正确.故选C.

解题模板　已知余弦型函数f(x)=Acos(ωx+φ)+B(A>0,ω>0)的部分图象,求其解析式的方法:A=,B=;根据图象找到周期,利用ω=求得ω的值;利用“五点”中的已知点,结合φ的取值范围,求得φ的值,进而得到解析式.

7.A　由题表可知y的最大值为4,最小值为-4,故A=4.由-=T,得T=π,∴ω==2,

∴y=4sin(2x+φ),∵其图象过点,

∴0=4sin,∴×2+φ=2kπ(k∈Z),解得φ=2kπ-(k∈Z),

∵|φ|<,∴φ=-.故选A.

8.C　由题图可知函数f(x)的最小正周期T=2×=,故ω==3.将代入解析式,得Acos=0,故+φ=+2kπ(k∈Z),所以φ=-+2(k-1)π(k∈Z),

则f(x)=Acos,

又f=-Acos=-,所以A=.

故f(x)=cos.

所以f(0)=cos=×=.故选C.

9.AC　由题图可知,A=2,函数f(x)的最小正周期T=4×=π,则ω==2.

又f=2cos=2,所以cos=1,

所以+φ=2kπ(k∈Z),

而|φ|<,所以φ=-,所以f(x)=2cos.将y=2cos x的图象上所有的点向右平移个单位长度,得到y=2cos的图象,再把所得图象上所有点的横坐标变为原来的,得到f(x)的图象;也可以将y=2cos x的图象上所有点的横坐标变为原来的,再将所得图象向右移个单位长度得到f(x)的图象.故选AC.

10.A　由题图及五点画图法可得A=1,ω·+φ=π,ω·+φ=,所以ω=2,φ=,

故f(x)=sin.

当x∈时,2x+∈,

故f(x)=sin∈,函数f(x)在区间上不是增函数,故A正确,C错误;

因为f=sin=-1,所以点不是函数f(x)的图象的对称中心,故B错误;

将函数y=cos 2x的图象向右平移个单位长度得到y=cos=cos=sin2x-+=sin的图象,故D错误.故选A.

11.解析　(1)列表:

描点、连线,得到图象如下:

(2)令2kπ-≤+≤2kπ+,k∈Z,得4kπ-≤x≤4kπ+,k∈Z,所以函数f(x)的单调递增区间为,k∈Z.

(3)当+=+2kπ(k∈Z),即x=+4kπ(k∈Z)时, f(x)取得最大值2.

故f(x)的最大值为2,取得最大值时x的取值集合为.

12.解析　(1)由题意作出f(x)的简图如图.

由图象知A=2,函数f(x)的最小正周期T=2×2π=4π,

∴ω==,

∴f(x)=2sin,

∴f(0)=2sin φ=1,即sin φ=,

又∵|φ|<,∴φ=,∴f(x)=2sin.

∵f(x0)=2sin=2,

∴x0+=+2kπ,k∈Z,

∴x0=4kπ+,k∈Z,

又(x0,2)是函数图象在y轴右侧的第一个最高点,

∴x0=.

(2)令-+2kπ≤x+≤+2kπ,k∈Z,得-+4kπ≤x≤+4kπ,k∈Z,

∴f(x)的单调递增区间为(k∈Z).

13.解析　(1)由题图知A=2,f(x)的最小正周期T=2×=π,所以ω==2.

由五点画图法,可得2×+φ=0,所以φ=.

所以f(x)=2sin.

(2)由题意得g(x)=2sin=-2cos,

故y=f(x)+g(x)=2sin-2cos=2sin.

令2sin=,得sin=.

因为0<x<,所以-<2x-<,

所以2x-=或2x-=或2x-=或2x-=,

所以x=或x=或x=或x=,

所以在给定区间内所有交点的横坐标之和为+++=.

能力提升练

1.B　由题意可得,将g(x)的图象上各点的横坐标变为原来的2倍,纵坐标不变,再向右平移个单位长度可得到f(x)的图象,故f(x)=sin=sin x.故选B.

2.A　∵f(x)=sin 2x+2cos2x-1=sin 2x+cos 2x=2sin,

∴g(x)=f=2sin2x-+=2sin.故选A.

3.D　若点A在函数f(x)的图象上,

则f=cos=1,

即+φ=2kπ,k∈Z,即φ=-+2kπ,k∈Z,

又|φ|<,所以φ=-,

所以f(x)=cos.

因为y=sin=cos=cos=cos,

所以只需将f(x)的图象向左平移个单位长度,即可得到y=sin的图象.故选D.

解题模板　三角函数的图象变换必须是同名函数才可以,若变换前后的函数名称不同,则要选择合适的诱导公式将其化为同名函数,再分析自变量的变化关系,得到变换的结果.

4.B　由题意可得, f(x-φ)=sin=cos=cos=cos的图象关于y轴对称,

∴+2φ=kπ,k∈Z,则φ=-,k∈Z,又φ>0,

∴φ的最小值为.故选B.

5.ABC　由T==π,得ω=2,∴f(x)=sin(2x+φ).

将f(x)的图象向左平移个单位长度后所得图象对应的函数为g(x)=f=sin.

由g(x)是偶函数,知+φ=+kπ,k∈Z,

又-<φ<,∴φ=.因此f(x)=sin.

∴f(0)=sin=,A正确; f=sin=1,是最大值,B正确; f=sin π=0,C正确;f=sin=≠±1,D错误.故选ABC.

6.AC　f=sin=-cos 3x,为偶函数,A正确.

f(π)=sin=sin =,B错误.

易知f(x)=sin的最大值为1,最小值为-1,若|f(x1)-f(x2)|=2,则f(x1)=1, f(x2)=-1或f(x1)=-1, f(x2)=1,

当f(x1)=1, f(x2)=-1时,3x1-=+2k1π,k1∈Z,3x2-=-+2k2π,k2∈Z,故x1-x2=+,k3∈Z,所以|x1-x2|的最小值为;

同理,当f(x1)=-1, f(x2)=1时,|x1-x2|的最小值为.故|x1-x2|的最小值为,C正确.

函数f(x)的图象向右平移个单位长度得到函数y=sin=sin(3x-π)=-sin 3x的图象,D错误.

故选AC.

7.C　将函数f(x)=2sin的图象向右平移4t(t>0)个单位长度,得到y=2sin的图象,再将图象上各点的横坐标缩短为原来的,得到y=2sin的图象,故g(x)=2sin.

对任意的x∈R,g(x)≥g恒成立,

则g(x)min=g,

所以sin=-1,即+-2t=-+2kπ,k∈Z,解得2t=-2kπ,k∈Z.

故g(x)=2sin=2sin,k∈Z.

g=2sin=-1≠±2,故A错误;

g=2sin≠±2,故B错误;

g=sin(-π)=0,所以g(x)的图象关于点对称,故C正确;

g=2sin=-≠0,故D错误.

故选C.

8.答案　

解析　由题图可得f(0)=sin φ=,

∵0<φ<π,∴φ=或φ=,

由于x=0在函数f(x)的单调递减区间内,所以φ=.

9.解析　(1)由题图可得A=1,=+=,所以T=π,则ω==2,所以f(x)=sin(2x+φ).因为f(x)的图象过点,所以2×+φ=+2kπ(k∈Z),即φ=+2kπ(k∈Z),又-<φ<,所以φ=,故f(x)=sin.

(2)结合题中图象及函数的最小正周期可知,函数f(x)的图象的对称轴方程为x=+(k∈Z).

令-+2kπ≤2x+≤+2kπ,k∈Z,

得-π+kπ≤x≤+kπ,k∈Z,

故函数f(x)的单调递增区间为(k∈Z).

(3)f(x)的图象向右平移个单位长度得到y=sin=sin的图象,故g(x)=sin.

作出y=g(x)在上的图象,如图所示:

因为g(x)=a-1在x∈上有两个不同的解,所以≤a-1<1,即≤a<2.故a的取值范围是.

10.解析　(1)由题图可得A=1,T=2×=2,则ω==π.

当x==时,f(x)取得最大值,

则π+φ=+2kπ(k∈Z),

所以φ=-+2kπ(k∈Z),

又因为|φ|<,所以φ=-.

(2)由(1)可知f(x)=sin,

令+2kπ≤πx-≤+2kπ,k∈Z,

解得+2k≤x≤+2k,k∈Z.

故f(x)的单调递减区间为(k∈Z).

取k=0,可得f(x)在[1,2]上的单调递减区间为.

(3)令f(x)=sin=0,则πx-=kπ,k∈Z,解得x=k+,k∈Z,

所以f(x)在上有两个零点.

因为f(x)的最小正周期为2,

所以若函数y=f(x)在区间[a,b]上恰有2 020个零点,则1 009×

2+1≤b-a<1 010×2+1,故b-a的取值范围为[2 019,2 021).