北师大版6 利用三角函数测高说课ppt课件

这是一份北师大版6 利用三角函数测高说课ppt课件，共9页。PPT课件主要包含了新知讲解，例题分析，解决问题，拓展提升，过程详解，课堂小结，课后巩固等内容，欢迎下载使用。
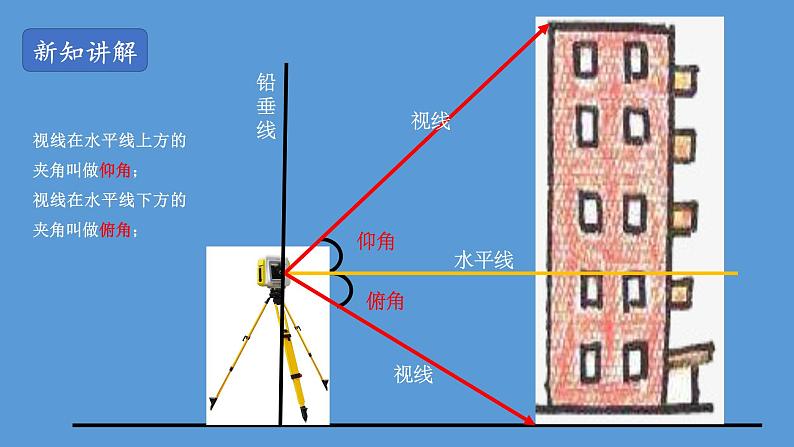
视线在水平线上方的夹角叫做仰角；视线在水平线下方的夹角叫做俯角；
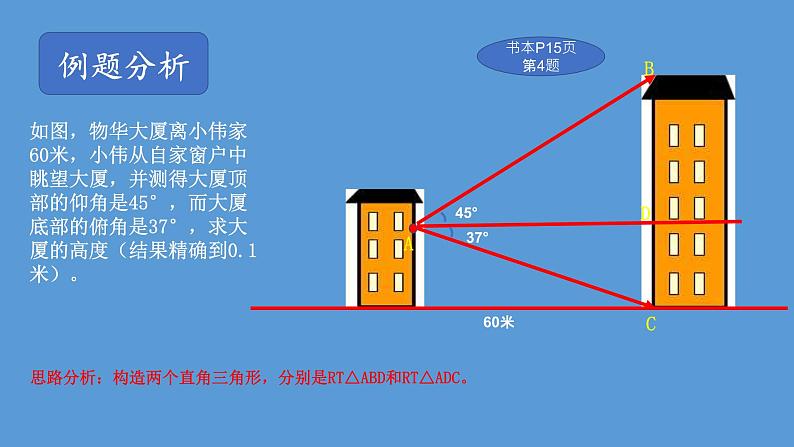
如图，物华大厦离小伟家60米，小伟从自家窗户中眺望大厦，并测得大厦顶部的仰角是45°，而大厦底部的俯角是37°，求大厦的高度（结果精确到0.1米）。
思路分析：构造两个直角三角形，分别是RT△ABD和RT△ADC。
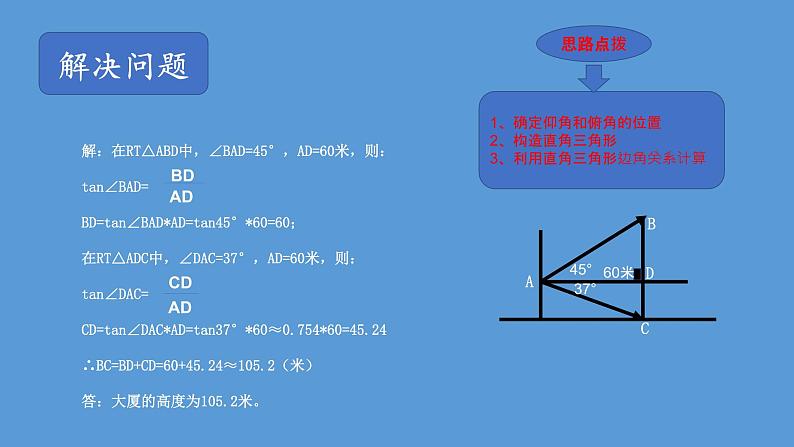
解：在RT△ABD中，∠BAD=45°，AD=60米，则：tan∠BAD= BD=tan∠BAD*AD=tan45°*60=60；在RT△ADC中，∠DAC=37°，AD=60米，则：tan∠DAC= CD=tan∠DAC*AD=tan37°*60≈0.754*60=45.24∴BC=BD+CD=60+45.24≈105.2（米）答：大厦的高度为105.2米。
（2020•河北区一模）如图，小李欲测量一棵古树MN的高度，小李在古树前方B点处测得树顶M处的仰角为35°．他径直走了8m后到达点A处，测得树顶M的仰角为23°．已知小李的眼睛距离地面的高度BD＝AC＝1.8m．求古树的高度MN和BN的长（结果取整数）．（参考数据：tan35°≈0.70，tan23°≈0.42．）
【分析】延长CD交MN于点E，根据题意可得EN＝BD＝AC＝1.8，CE＝AN，CD＝AB＝8，DE＝BN，设BN＝x，根据锐角三角函数即可求出古树的高度MN和BN的长．
仰角：当从低处测高处的目标时，视线与水平线所形成的锐角称为仰角；俯角：当从高处观测低处目标时，视线与水平线所成的锐角称为俯角；
1、确定仰角和俯角的位置；2、构造直角三角形；3、利用直角三角形边角关系计算；
（2020•成都模拟）兴隆湖是成都天府新区著名的生态绿地工程．在一次户外综合实践活动中，小明同学所在的兴趣小组用无人机航拍测量云图广场A与南山码头B的直线距离．由于无人机控制距离有限，为了安全，不能直接测量，他们采用如下方法：如图，小明在云图广场A的正上方点C处测得南山码头B的俯角α＝17.09°；接着无人机往南山码头B方向水平飞行0.9千米到达点D处，测得此时南山码头B的俯角β＝45°．已知AC⊥AB，CD∥AB，请根据测量数据计算A，B两地的距离．（结果精确到0.1km，参考数据：sinα≈0.29，tanα≈0.31，sinβ≈0.71）