





还剩15页未读,
继续阅读
初中数学 北师大版 九年级上册 《投影与视图》回顾与思考 课件
展开
这是一份初中数学 北师大版 九年级上册 《投影与视图》回顾与思考 课件,共23页。
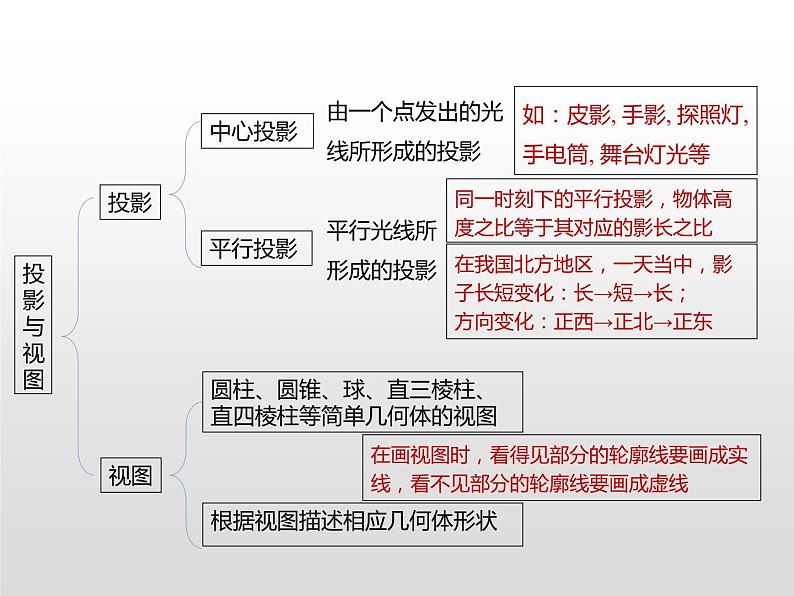
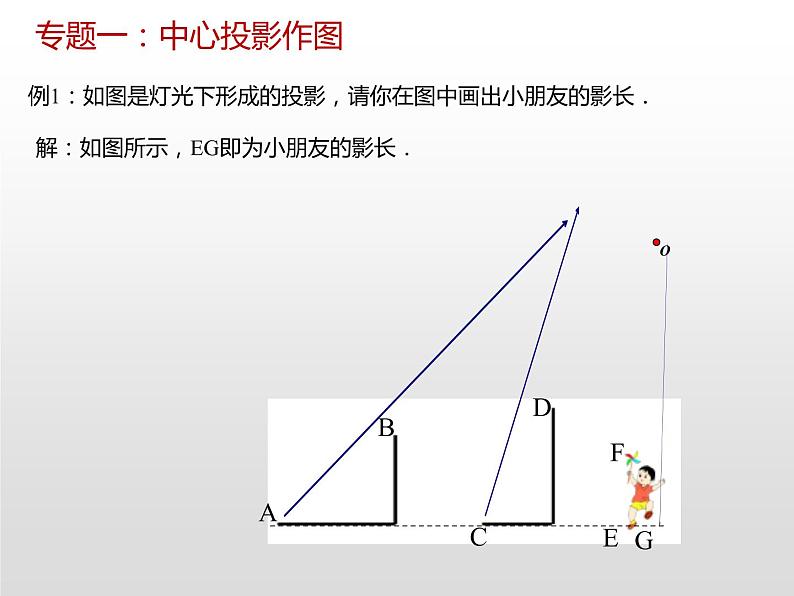
第五章 投影和视图复习课走进生活走进生活走进艺术走进艺术回答问题1.生活中有哪些中心投影和平行投影现象? 举例说明.2.中心投影和平行投影的特点分别是什么? 举例说明灯光及其形成的影子、太阳光及其形成的影子的应用. 3.什么是几何体的三种视图?圆柱、圆锥、球、正方体的三种视图分别是什么?如何画直棱柱的三种视图?4.一个几何体的三种视图有什么特征?它与实物有什么联系? 5. 学了本章后,你有哪些收获和体会?与同伴进行交流.6.用你自己喜欢的方式梳理本章的知识. 投影视图中心投影平行投影圆柱、圆锥、球、直三棱柱、直四棱柱等简单几何体的视图根据视图描述相应几何体形状投影与视图如:皮影, 手影, 探照灯, 手电筒, 舞台灯光等由一个点发出的光线所形成的投影同一时刻下的平行投影,物体高度之比等于其对应的影长之比平行光线所形成的投影在我国北方地区,一天当中,影子长短变化:长→短→长;方向变化:正西→正北→正东在画视图时,看得见部分的轮廓线要画成实线,看不见部分的轮廓线要画成虚线专题一:中心投影作图例1:如图是灯光下形成的投影,请你在图中画出小朋友的影长.解:如图所示,EG即为小朋友的影长.ABCDEFG点光源位置的确定由两个物体的投影,即可得到点光源位置,确定方法为: 1.分别连接两个物体顶端与它的投影顶端,并延长交于一点.该交点即为点光源位置. 2.若要作第三个物体的投影,需要连接点光源与该物体顶端,并延长使与地面相交,那么该点和该物体底端的连线即该物体的投影.专题二:利用光沿直线传播的性质构造相似三角形测高例2. 小明想测量路灯杆上灯泡的高度,就拿起一根2m长的竹竿伸向路灯,但无论如何也触不到.于是他走到路灯旁的一个地方,竖起竹竿,量得竹竿的影长正好是1m;然后他沿着影子的方向走出两根竹竿的长度(即4 m),又竖起竹竿,测得竹竿的影长正好是一根竹竿的长度(即2m),你知道小明将怎样计算灯泡的高度吗?专题二:利用光沿直线传播的性质构造相似三角形测高解:如图所示,AE是第一次竖起竹竿的位置,此时有△AEC∽△POC,AE=2m,AC=1m.于是有 ,即 , ∴CP= ,AP= -1.BF是第二次竖竹竿的位置,此时有△BFD∽△POD,BF=2m,BD=2m,AB=4m.于是有 ,即 ,∴OP=DP.∴DP=DB+BC+CP=DB+BA+AP,即OP=2+4+ -1.解得:OP=10.故灯泡的高为10 m.专题二:利用光沿直线传播的性质构造相似三角形测高专题二:利用光沿直线传播的性质构造相似三角形测高例3:如下图所示,墙边有甲、乙两根木杆,乙木杆的影子刚好不落在墙上.(1)画出太阳光线及甲木杆的影子;(2)当甲木杆高为2 m,乙木杆高为1.5 m,乙木杆到墙的距离为1.5 m时,求甲木杆的影长.专题二:利用光沿直线传播的性质构造相似三角形测高解: (1)如图所示,用AB表示乙木杆(A为顶部),CD表示甲木杆,墙角用E表示,连接AE,过C作AE的平行线交地面于点F,则直线AE,CF是光线,DF是甲木杆的影子.(2)图中△ABE∽△CDF,则有 ,即 .解得DF=2米.即甲木杆的影长为2米.专题三:几何体与三视图的相互转化例4:(1)如图所示,在一个透明的玻璃正方体内镶嵌了一条铁丝,请指出图①中的两个图是正方体的哪种视图.解:(1)由三视图的定义可以看出,图①分别是正方体的俯视图、主视图.专题三:几何体与三视图的相互转化例4:(2)如图②所示,粗线表示嵌在玻璃正方体内的一根铁丝,画出该正方体的主视图、左视图、俯视图.解:(2)几何体的三视图如图所示.三种视图的作法由几何体确定三种视图时,一定要理清以下概念:主视图是从几何体的正面观察到的平面图形;左视图是从几何体的左面观察到的平面图形;俯视图是从几何体的上面观察到的平面图形;长对正、高平齐、宽相等由三视图计算几何体的体积或表面积的一般步骤:(1)首先要根据三视图描述几何的形状(或画出表面展开图);(2)再根据三视图“长对正、高平齐、宽相等”的关系和轮廓线的位置确定各个方向的尺寸;(3)最后用面积公式求出表面积或用体积公式求体积.专题一:中心投影作图针对训练1:如图,电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路的一侧,AB、CD、EF是三个标杆:(1)请画出路灯O的位置;(2)画出标杆EF在路灯下的影子FH.解:(1)如图,点O为所作; (2)如图,FH为所作.H专题二:利用光沿直线传播的性质构造相似三角形测高针对训练2:我国《道路交通安全法》第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”.如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?解:如图所示:延长AB,∵CD∥AB,∴∠CAB=30°,∠CBF=60°,∴∠BCA=60°-30°=30°,即∠BAC=∠BCA,∴BC=AB=3m,在Rt△BCF中,BC=3m,∠CBF=60°,∴BF= BC=1.5m,故x=BF-EF=1.5-0.8=0.7(m),答:这时汽车车头与斑马线的距离x是0.7m.专题三:几何体与三视图的相互转化针对训练4:下图是一几何体的两种视图,请你指出其中的错误,并把它们改正过来.解:主视图中多了一段实线,左视图中上下矩形宽不应相同. 正确的主视图和左视图如右图所示:专题三:几何体与三视图的相互转化针对训练5:一个立体图形的三视图如图所示,根据图中的数据得这个立体图形的表面积为( )A.2π B.6π C.7π D.8π解:由立体图形的三视图可知该立体图形为平放的圆柱体,底面半径r=1,高为3,故其表面积S=2πr2+2πr•3=2π•12+2π•1•3=8π.故选D.D中心投影和平行投影;常见几何体的三种视图;几何体和三种视图的相互转化.本章的重点知识:
第五章 投影和视图复习课走进生活走进生活走进艺术走进艺术回答问题1.生活中有哪些中心投影和平行投影现象? 举例说明.2.中心投影和平行投影的特点分别是什么? 举例说明灯光及其形成的影子、太阳光及其形成的影子的应用. 3.什么是几何体的三种视图?圆柱、圆锥、球、正方体的三种视图分别是什么?如何画直棱柱的三种视图?4.一个几何体的三种视图有什么特征?它与实物有什么联系? 5. 学了本章后,你有哪些收获和体会?与同伴进行交流.6.用你自己喜欢的方式梳理本章的知识. 投影视图中心投影平行投影圆柱、圆锥、球、直三棱柱、直四棱柱等简单几何体的视图根据视图描述相应几何体形状投影与视图如:皮影, 手影, 探照灯, 手电筒, 舞台灯光等由一个点发出的光线所形成的投影同一时刻下的平行投影,物体高度之比等于其对应的影长之比平行光线所形成的投影在我国北方地区,一天当中,影子长短变化:长→短→长;方向变化:正西→正北→正东在画视图时,看得见部分的轮廓线要画成实线,看不见部分的轮廓线要画成虚线专题一:中心投影作图例1:如图是灯光下形成的投影,请你在图中画出小朋友的影长.解:如图所示,EG即为小朋友的影长.ABCDEFG点光源位置的确定由两个物体的投影,即可得到点光源位置,确定方法为: 1.分别连接两个物体顶端与它的投影顶端,并延长交于一点.该交点即为点光源位置. 2.若要作第三个物体的投影,需要连接点光源与该物体顶端,并延长使与地面相交,那么该点和该物体底端的连线即该物体的投影.专题二:利用光沿直线传播的性质构造相似三角形测高例2. 小明想测量路灯杆上灯泡的高度,就拿起一根2m长的竹竿伸向路灯,但无论如何也触不到.于是他走到路灯旁的一个地方,竖起竹竿,量得竹竿的影长正好是1m;然后他沿着影子的方向走出两根竹竿的长度(即4 m),又竖起竹竿,测得竹竿的影长正好是一根竹竿的长度(即2m),你知道小明将怎样计算灯泡的高度吗?专题二:利用光沿直线传播的性质构造相似三角形测高解:如图所示,AE是第一次竖起竹竿的位置,此时有△AEC∽△POC,AE=2m,AC=1m.于是有 ,即 , ∴CP= ,AP= -1.BF是第二次竖竹竿的位置,此时有△BFD∽△POD,BF=2m,BD=2m,AB=4m.于是有 ,即 ,∴OP=DP.∴DP=DB+BC+CP=DB+BA+AP,即OP=2+4+ -1.解得:OP=10.故灯泡的高为10 m.专题二:利用光沿直线传播的性质构造相似三角形测高专题二:利用光沿直线传播的性质构造相似三角形测高例3:如下图所示,墙边有甲、乙两根木杆,乙木杆的影子刚好不落在墙上.(1)画出太阳光线及甲木杆的影子;(2)当甲木杆高为2 m,乙木杆高为1.5 m,乙木杆到墙的距离为1.5 m时,求甲木杆的影长.专题二:利用光沿直线传播的性质构造相似三角形测高解: (1)如图所示,用AB表示乙木杆(A为顶部),CD表示甲木杆,墙角用E表示,连接AE,过C作AE的平行线交地面于点F,则直线AE,CF是光线,DF是甲木杆的影子.(2)图中△ABE∽△CDF,则有 ,即 .解得DF=2米.即甲木杆的影长为2米.专题三:几何体与三视图的相互转化例4:(1)如图所示,在一个透明的玻璃正方体内镶嵌了一条铁丝,请指出图①中的两个图是正方体的哪种视图.解:(1)由三视图的定义可以看出,图①分别是正方体的俯视图、主视图.专题三:几何体与三视图的相互转化例4:(2)如图②所示,粗线表示嵌在玻璃正方体内的一根铁丝,画出该正方体的主视图、左视图、俯视图.解:(2)几何体的三视图如图所示.三种视图的作法由几何体确定三种视图时,一定要理清以下概念:主视图是从几何体的正面观察到的平面图形;左视图是从几何体的左面观察到的平面图形;俯视图是从几何体的上面观察到的平面图形;长对正、高平齐、宽相等由三视图计算几何体的体积或表面积的一般步骤:(1)首先要根据三视图描述几何的形状(或画出表面展开图);(2)再根据三视图“长对正、高平齐、宽相等”的关系和轮廓线的位置确定各个方向的尺寸;(3)最后用面积公式求出表面积或用体积公式求体积.专题一:中心投影作图针对训练1:如图,电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路的一侧,AB、CD、EF是三个标杆:(1)请画出路灯O的位置;(2)画出标杆EF在路灯下的影子FH.解:(1)如图,点O为所作; (2)如图,FH为所作.H专题二:利用光沿直线传播的性质构造相似三角形测高针对训练2:我国《道路交通安全法》第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”.如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?解:如图所示:延长AB,∵CD∥AB,∴∠CAB=30°,∠CBF=60°,∴∠BCA=60°-30°=30°,即∠BAC=∠BCA,∴BC=AB=3m,在Rt△BCF中,BC=3m,∠CBF=60°,∴BF= BC=1.5m,故x=BF-EF=1.5-0.8=0.7(m),答:这时汽车车头与斑马线的距离x是0.7m.专题三:几何体与三视图的相互转化针对训练4:下图是一几何体的两种视图,请你指出其中的错误,并把它们改正过来.解:主视图中多了一段实线,左视图中上下矩形宽不应相同. 正确的主视图和左视图如右图所示:专题三:几何体与三视图的相互转化针对训练5:一个立体图形的三视图如图所示,根据图中的数据得这个立体图形的表面积为( )A.2π B.6π C.7π D.8π解:由立体图形的三视图可知该立体图形为平放的圆柱体,底面半径r=1,高为3,故其表面积S=2πr2+2πr•3=2π•12+2π•1•3=8π.故选D.D中心投影和平行投影;常见几何体的三种视图;几何体和三种视图的相互转化.本章的重点知识:
相关资料
更多









