初中数学湘教版八年级上册2.5 全等三角形公开课ppt课件

课题名

全等三角形判定ASA和AAS

教学目标

知识与技能：理解掌握三角形全等判定ASA和AAS的内涵，并能灵活运用。

过程与方法：通过操作、观察、交流、逻辑推理、总结归纳等活动，探究三角形全等判定ASA和AAS的内涵及应用的技巧。

情感态度：培养学生的动手操作能力、观察能力、理解能力、逻辑推理能力、总结归纳能力，获得必需的数学知识，激发学生的学习兴趣。

教学重点

三角形全等判定ASA和AAS的内涵及应用技巧。

教学难点

三角形全等判定ASA和AAS的内涵及应用技巧。

教学准备

教师准备：制作《全等三角形判定ASA和AAS》课件及剪取多组形状不一的全等图形。

学生准备：课前预习课本第79～82页的《全等三角形判定ASA和AAS》及白纸、剪刀。

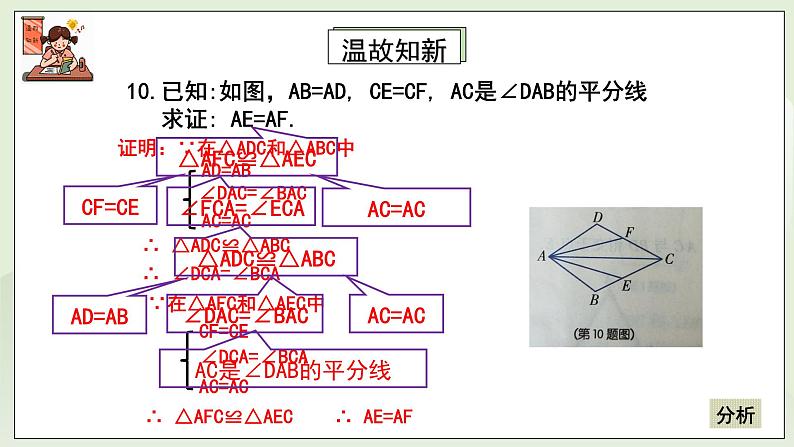
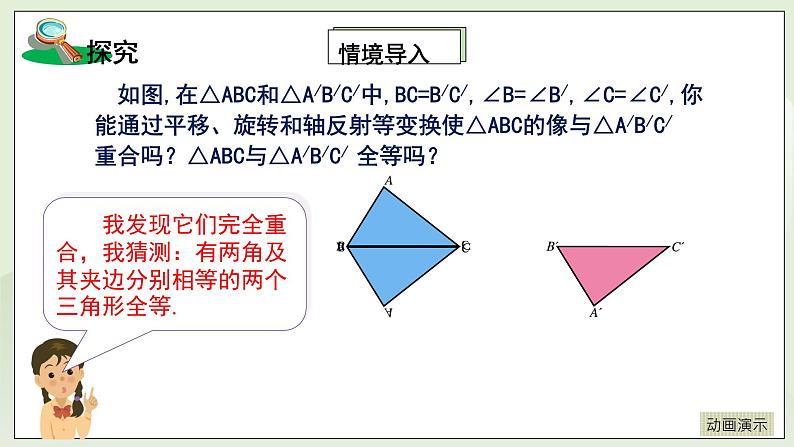
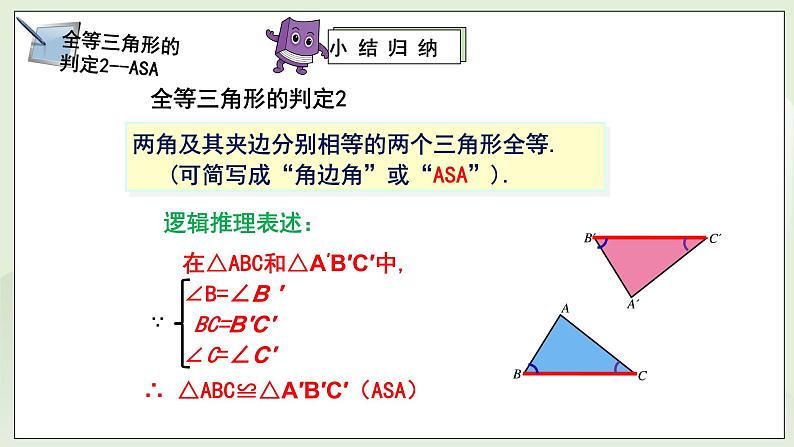
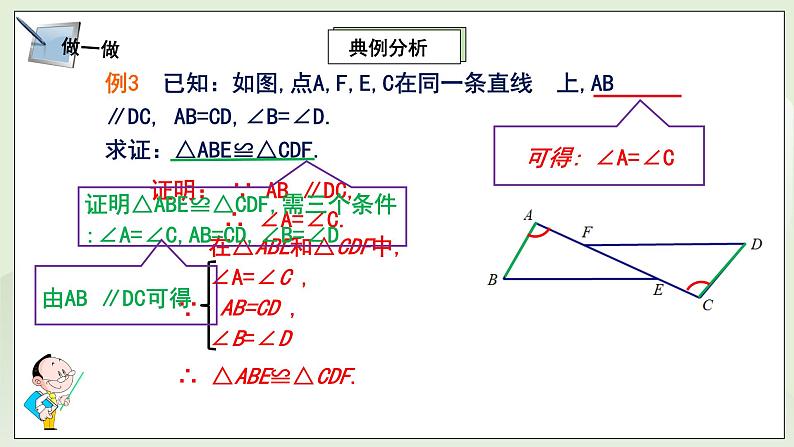
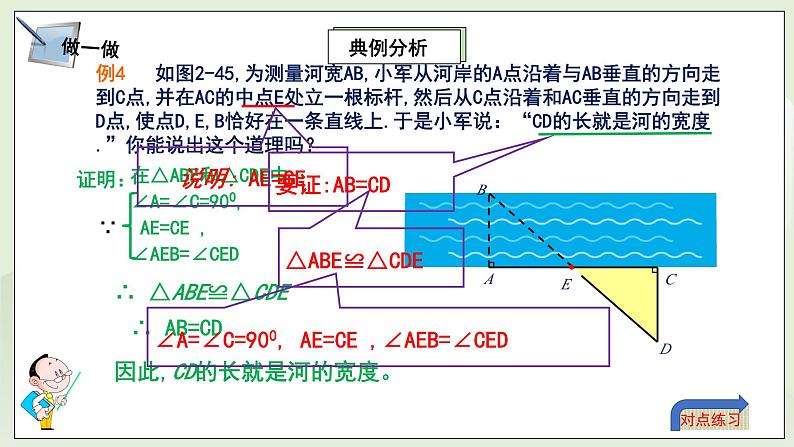
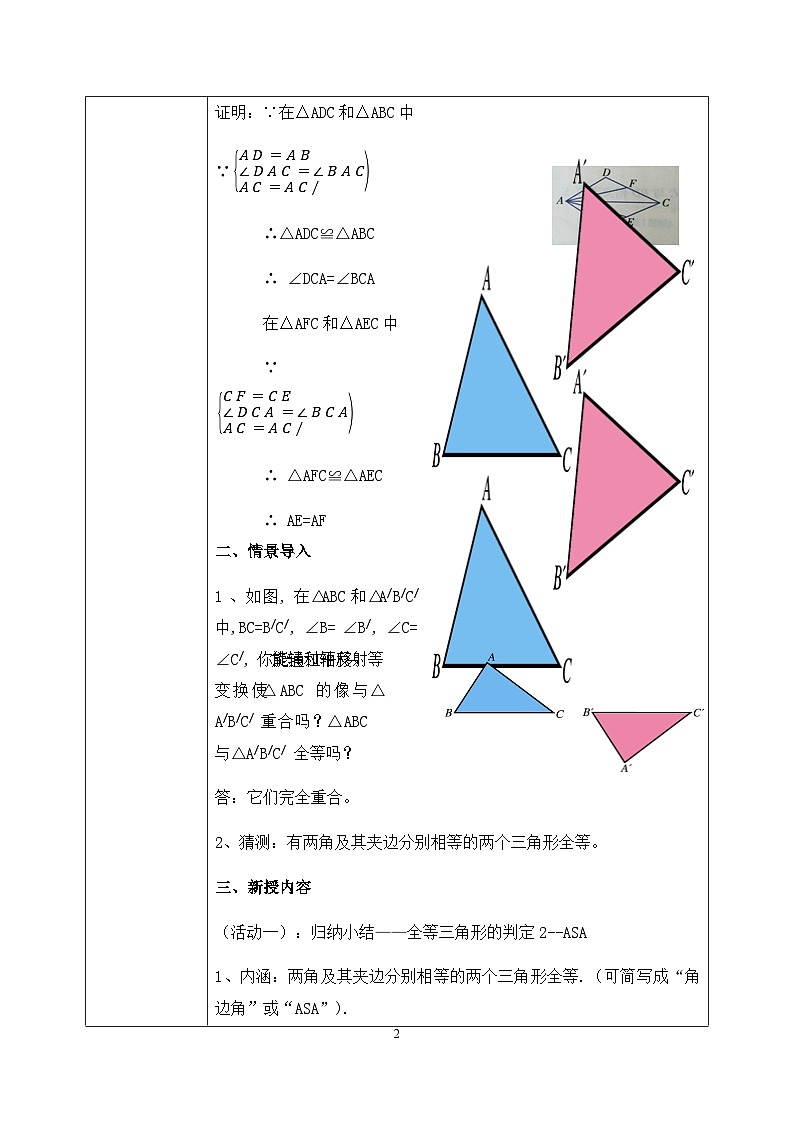
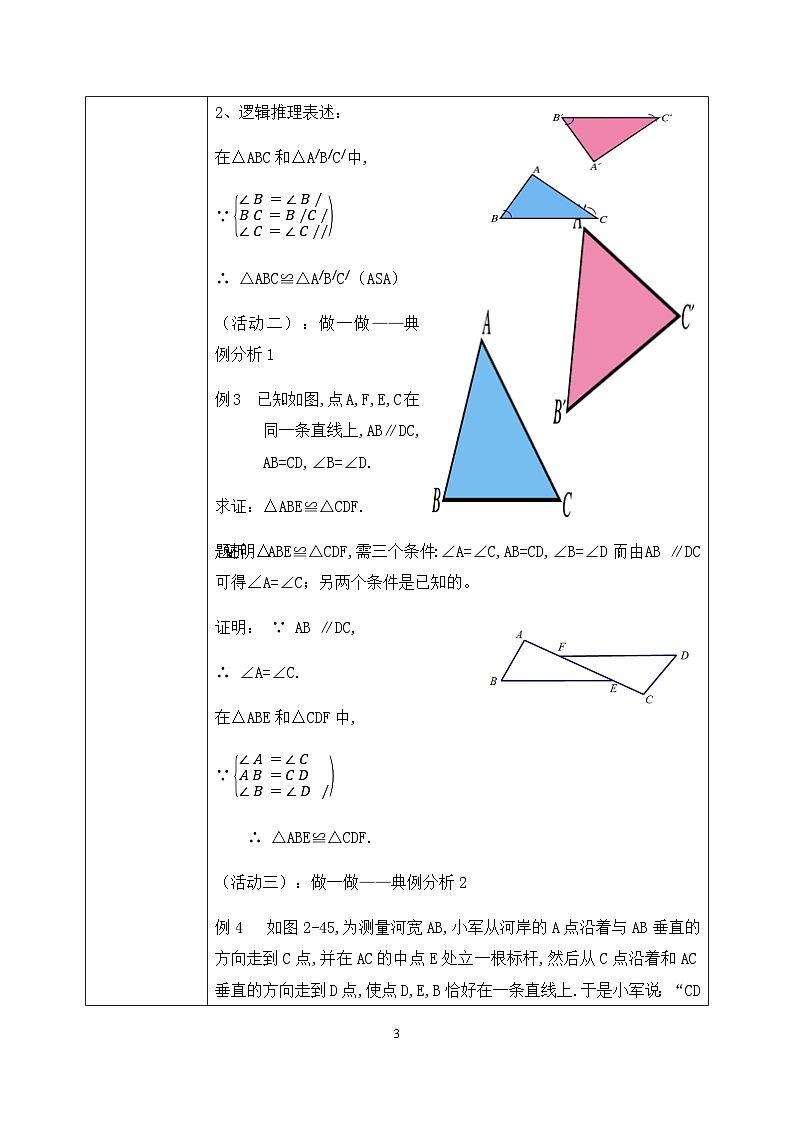
教学过程

一、温故知新

1、提问：我们已经学了哪种判定两个三角形全等的方法？

答：全等三角形的判定1（SAS)：两边及其夹角分别相等的两个三角形全等。

§口决:两边一角夹中间.

2、已知:如图，AB=AD, CE=CF, AC是∠DAB的平分线

   求证: AE=AF.

证明：∵在△ADC和△ABC中

∵

∴△ADC≌△ABC

∴ ∠DCA=∠BCA

在△AFC和△AEC中

∵

∴ △AFC≌△AEC

∴ AE=AF
二、情景导入

1、如图,在△ABC和△A/B/C/中,BC=B/C/,∠B=∠B/,∠C=∠C/,你能通过平移、旋转和轴反射等变换使△ABC的像与△A/B/C/ 重合吗？△ABC与△A/B/C/ 全等吗？

答：它们完全重合。

2、猜测：有两角及其夹边分别相等的两个三角形全等。

三、新授内容

（活动一）：归纳小结——全等三角形的判定2--ASA

1、内涵：两角及其夹边分别相等的两个三角形全等.（可简写成“角边角”或“ASA”).

2、逻辑推理表述：

在△ABC和△A/B/C/中,

∵

∴ △ABC≌△A/B/C/（ASA）

（活动二）：做一做——典例分析1

例3  已知：如图,点A,F,E,C在同一条直线上,AB∥DC, AB=CD,∠B=∠D.

求证：△ABE≌△CDF.

题析：证明△ABE≌△CDF,需三个条件:∠A=∠C,AB=CD,∠B=∠D ；而由AB ∥DC可得∠A=∠C；另两个条件是已知的。

证明： ∵ AB ∥DC,

∴ ∠A=∠C.

在△ABE和△CDF中,

∵

∴ △ABE≌△CDF.

（活动三）：做一做——典例分析2

例4   如图2-45,为测量河宽AB,小军从河岸的A点沿着与AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着和AC垂直的方向走到D点,使点D,E,B恰好在一条直线上.于是小军说：“CD的长就是河的宽度.”你能说出这个道理吗？

题析：“CD的长就是河的宽度”说明要证:AB=CD 。可通过△ABE≌△CDE；而证明△ABE≌△CDE需要三个条件：∠A=∠C=900, AE=CE ,∠AEB=∠CED。

证明：在△ABE和△CDE中,

∵

∴ △ABE≌△CDE

∴ AB=CD，即CD的长就是河的宽度。

（活动四）：动脑筋--探究全等三角形判定3(AAS)

如图,在△ABC和 △A/B/C/中,如果∠A=∠A/,∠B=∠B/, BC=B/C/.那么△ABC和△A/B/C/全等吗？

题析：要证明“△ABC和△A/B/C/全等”需三个条件：∠B=∠B/, BC=B/C/, ∠C =∠C/。已知了两个条件：∠B=∠B/, BC=B/C/。

而通“∠A=∠A/,∠B=∠B/”可得∠C =∠C/。

（活动五）：动脑筋

1、全等三角形的判定3的内涵：两角分别相等且其中一组等角的对边相等的两个三角形全等.   (可简写成“角角边”或“AAS”)。

2、逻辑推理表述：

在△ABC和△A/B/C/中,

∵

∴ △ABC≌△A/B/C/。

（活动六）：火眼金睛

下列哪组三角形全等

§解题技巧：运用“两角一边”证三角形全等时，一定要分清根据是“ASA”还是“AAS”,两三角形角边排列顺序一定要一致

（活动六）：做一做——典例分析3

例5 已知：如图, ∠B=∠D,∠1=∠2.

       求证：△ABC≌△ADC.

证明：∵ ∠1=∠2

∴ ∠ACB=∠ACD (等角的补角相等).

在△ABC和△ADC中

∵

∴ △ABC≌△ADC

（活动七）：做一做——典例分析4

例6 已知：如图,点B,F,C,E在同一条直线上,AC∥FD,

∠A=∠D,BF=EC. 求证：△ABC≌△DEF.

题析：要证“△ABC≌△DEF”，需要三个条件：∠A=∠D,∠ACB=∠DFE, BC=EF。通过“AC∥FD”可得：∠ACB=∠DFE；通过“BF=EC”可得：BC=EF。

证明：∵ AC∥FD，∴ ∠ACB=∠DFE

∵ BF=EC,

∴ BF+FC=EC+FC,即BC=EF

在△ABC和△DEF中,

∵

∴ △ABC≌△DEF.

§证明两个三角形全等时，书写证明过程时需注意什么？

1)证明两个三角形全等所需的条件应按判定定理所有边、角顺序书写;

2)“边角边”中的“角”必须是两边的夹角;

3)“角边角”中的“边”必须是两角的夹边.

4)“角角边”时，两三角形角边排列顺序一定要一致.

口决：两边一角夹中间，两角一边任意选。

四、课堂小测

1. 如图，工人师傅不小心把一块三角形玻璃打碎成三块，现要到玻璃店重新配一块与原来一样的三角形玻璃，只允许带其中的一块玻璃碎片去. 请问应带哪块玻璃碎片去？为什么？

因为只有这块玻璃可以测量出得到整块三角形玻璃的两个角及这两个角的夹边。根据“ASA”定理就可以重新配一块与原来一样的三角形玻璃。

2. 已知：如图△ABC≌△A/B/C/，CF,C/F/,分别是∠ACB  和∠A/C/B/的平分线.

  求证：CF=C/F/

证明：∵ △ABC≌△A/B/C/

∴AC=A/C/，∠A=∠A/,∠ACB=∠A/C/B/

又∵ ∠ACF =∠ACB,  ∠A/C/F/=∠A/C/B/.

∴ ∠ACF = ∠A/C/F/

在△ACF和△A/C/F/中,

∵

∴ △ACF≌△A/C/F/

∴ CF=C/F/

3. 已知：如图，∠1=∠2，AD=AE.

  求证：△ADC≌△AEB.

证明:∵ 在△ADC 和△AEB中，

∵

∴ △ADC≌△AEB（AAS）

4. 已知：在△ABC中，∠ABC =∠ACB，BD⊥AC于点D，CE⊥AB于点E.  

  求证：BD=CE.

证明:∵ 在Rt△BEC和Rt△CDB中

∴ △BEC≌ △CDB（AAS）,∴  BD=CE

布置作业

课作：P87  习题2.5第3、5题

家作:P88   习题2.5第4、11题及并预习课本P83~P84

板书设计

教学反思

本节课通过操作、观察、交流、逻辑推理、探究学习了三角形全等判定ASA和AAS的由来。其中三角形全等判定ASA和AAS的应用技巧是本节的教学重、难点，教学中需要通过实例培训学生几何分析能力和解题思路。