




人教版九年级上册第二十四章 圆综合与测试一课一练
展开专题06 垂径定理重难点题型分类
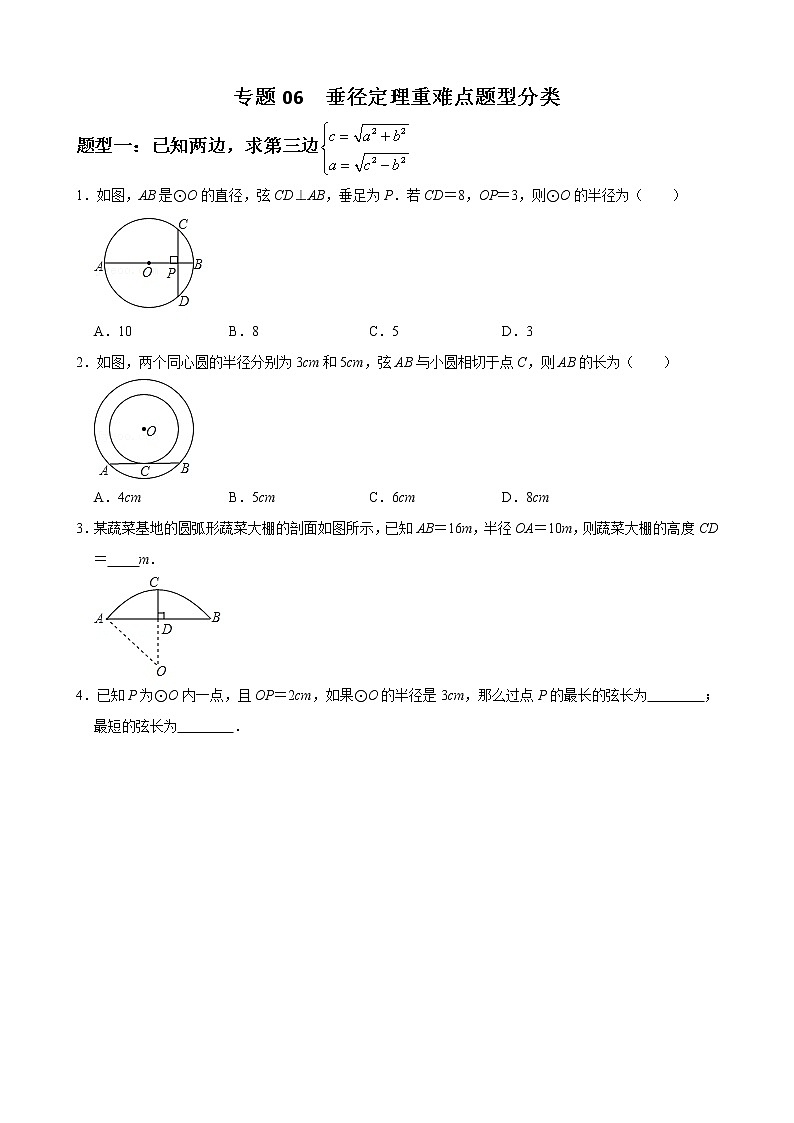
题型一:已知两边,求第三边
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为( )
A.10 B.8 C.5 D.3
【解答】解:连接OC,∵CD⊥AB,CD=8,∴PC=CD=×8=4,在Rt△OCP中,
∵PC=4,OP=3,∴OC===5.故选:C.
2.如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,则AB的长为( )
A.4cm B.5cm C.6cm D.8cm
【解答】解:连接OC和OB,∵弦AB与小圆相切,∴OC⊥AB,在Rt△OBC中,BC===4,∴AB=2BC=8cm.
故选:D.
3.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则蔬菜大棚的高度CD= m.
【解答】解:∵CD是中间柱,即=,∴OC⊥AB,∴AD=BD=AB=×16=8(m),
∵半径OA=10m,在Rt△AOD中,OD==6(m),∴CD=OC﹣OD=10﹣6=4(m).
故答案为:4
4.已知P为⊙O内一点,且OP=2cm,如果⊙O的半径是3cm,那么过点P的最长的弦长为 ;最短的弦长为 .
【解答】解:如图,AB是过点P最长的弦,是圆的一条直径,所以AB=6cm.CD是过点P最短的弦,CD⊥OP,在Rt△OPD中,PD2=OD2﹣OP2=9﹣4=5,∴PD=,CD=2.所以对短的弦长为2cm.
故答案是:6cm,2cm.
5.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为( )
A. B. C. D.
【解答】解:连接OA,OB,OC,作CH垂直于AB于H.∵AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,∴BE=AB=4,CF=CD=3,∴OE===3,OF===4,∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7,
在Rt△BCH中根据勾股定理得到BC===7,即PA+PC的最小值为7.
故选:A.
6.如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系,该圆弧所在圆的圆心为点D.
(1)写出点的坐标:C 、D ;
(2)⊙D的半径= (结果保留根号).
【解答】解:(1)C的坐标是(6,2),D的坐标是(2,0);
(2)在直角△OBE中,OB==2.
题型二:已知一边和一特殊角
7.如图,⊙O的直径AB垂直于弦CD,垂足是点E,∠CAO=22.5°,OC=6,则CD的长为( )
A.6 B.3 C.6 D.12
【解答】解:∵CD⊥AB,∴CE=DE,∵∠BOC=2∠A=2×22.5°=45°,
∴△OCE为等腰直角三角形,∴CE=OC=×6=3,∴CD=2CE=6.
故选:A.
8.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC,若∠CAB=22.5°,CD=8cm,则⊙O的半径为( )
A.8cm B.4cm C.4cm D.5cm
【解答】解:连接OC,如图所示:∵AB是⊙O的直径,弦CD⊥AB,∴CE=DE=CD=4cm,
∵OA=OC,∴∠A=∠OCA=22.5°,∵∠COE为△AOC的外角,∴∠COE=45°,∴△COE为等腰直角三角形,∴OC=CE=4cm,
故选:C.
9.如图,⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=60°.
(1)求点O到弦CD的距离;
(2)求弦CD的长.
【解答】解:(1)设OF的长为点O到弦CD的距离,∵AE=1cm,EB=5cm,∴AB=6cm,∴OA=OB=3cm,∴OE=OA﹣AE=2cm,∵在Rt△OFE中,∠OFE=90°,OE=2cm,∠DEB=60°,∴∠FOE=30°,∴EF=OE=1cm,OF===(cm),
即点O到弦CD的距离是cm;
(2)连接OD,在Rt△OFD中,∠OFD=90°,OD=OA=3cm,OF=cm,
由勾股定理得:DF===(cm),∵OF⊥DC,OF过O,∴DF=CF,
即CD=2DF=2cm.
题型三:已知一边,设半径为,第三边为“几”或“几”,列方程
10.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O的半径为( )
A.8 B.10 C.16 D.20
【解答】解:连接OC,如图所示:∵CD⊥AB,∴CE=CD=6,
设⊙O的半径为x,则OE=x﹣2,在Rt△OEC中,由勾股定理得:(x﹣2)2+62=x2
解得:x=10,即⊙O的半径为10,故选:B.
11.一种花边是如图的弓形组成的,弓形的高(弧的中点到弦的距离)CD长为2,弦AB=8,则的半径长为( )
A. B. C.6 D.5
【解答】解:设弧ACB所在圆的圆心为O,连接OC、OA,则OC与AB的交点即为D点,如图所示:
在Rt△OAD中,设OA=x,则OD=x﹣CD=x﹣2,AD=AB=4,∴OA2=OD2+AD2,
即x2=(x﹣2)2+42,解得x=5;故选:D.
12.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)已知:AB=16,CD=4.求(1)中所作圆的半径.
【解答】解:(1)如图所示:
(2)∵AB=16,CD=4,CD⊥AB,∴AD=BD=8,设半径为x,得:x2=82+(x﹣4)2,
解得:x=10.
13.如图,圆柱形油槽内原有积油的水平面宽CD=60cm,油深为10cm.若油面上升10cm,则此时油面宽AB为多少?(教材124页第10题改编)
【解答】解:作OE⊥CD于点E,交AB于点F.则CE=DE=×60=30(cm),
设半径是r,则OE=r﹣10.在直角△OCE中,OC2=OE2+CE2,即r2=302+(r﹣10)2,
解得:r=50.则OF=50﹣10﹣10=30(cm),
在直角△AOF中,AF===40(cm),
又∵OE⊥AB,∴AB=2AF=80(cm).
14.如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.求:
(1)桥拱的半径.
(2)现有一轮船宽60米,船舱顶部为长方形并高出水面9米要经过这里,这艘轮船能顺利通过吗?
【解答】解:(1)如图,点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
则由垂径定理知,点F是AB的中点,AF=FB=AB=40,EF=ED﹣FD=AE﹣DF,
由勾股定理知,AE2=AF2+EF2=AF2+(AE﹣DF)2,设圆的半径是r,则:r2=402+(r﹣20)2,
解得:r=50;
(2)如图,货船能顺利通过这座拱桥.理由:连接EM,设MD=30米.
∵DE⊥MN,EF=50﹣20=30(m),在Rt△DEM中,DE==40(米),
∵DF=DE﹣EF=40﹣30=10(米)∵10米>9米,
∴货船能顺利通过这座拱桥.
初中数学人教版九年级上册第二十一章 一元二次方程综合与测试达标测试: 这是一份初中数学人教版九年级上册第二十一章 一元二次方程综合与测试达标测试,文件包含专题02韦达定理重难点题型分类解析版-人教版doc、专题02韦达定理重难点题型分类原卷版-人教版doc等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
初中数学人教版九年级上册第二十二章 二次函数综合与测试练习: 这是一份初中数学人教版九年级上册第二十二章 二次函数综合与测试练习,文件包含专题03二次函数小题重难点题型分类解析版-人教版doc、专题03二次函数小题重难点题型分类原卷版人教版doc等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
数学九年级上册第二十四章 圆综合与测试精练: 这是一份数学九年级上册第二十四章 圆综合与测试精练,文件包含专题08切线的性质与判定重难点题型分类解析版人教版doc、专题08切线的性质与判定重难点题型分类原卷版-人教版doc等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。













