内蒙古通辽市三年（2020-2022）中考数学真题分类汇编-03解答题

这是一份内蒙古通辽市三年（2020-2022）中考数学真题分类汇编-03解答题，共44页。试卷主要包含了0﹣2cs30°+|3﹣|，÷，其中x满足x2﹣x﹣2＝0，解方程，用※定义一种新运算等内容，欢迎下载使用。
内蒙古通辽市三年（2020-2022）中考数学真题分类汇编-03解答题
一．实数的运算（共1小题）
1．（2021•通辽）计算：（）﹣1+（π﹣3）0﹣2cos30°+|3﹣|．
二．分式的化简求值（共1小题）
2．（2021•通辽）先化简，再求值：（+x﹣1）÷，其中x满足x2﹣x﹣2＝0．
三．解分式方程（共1小题）
3．（2020•通辽）解方程：＝．
四．分式方程的应用（共1小题）
4．（2021•通辽）为做好新冠疫情的防控工作，某单位需购买甲、乙两种消毒液，经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元，该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液．
（1）求甲、乙两种消毒液的零售价分别是每桶多少元？
（2）由于疫情防控进入常态化，该单位需再次购买两种消毒液共300桶，且甲种消毒液的桶数不少于乙种消毒液桶数的．由于购买量大，甲、乙两种消毒液分别获得了20元/桶、15元/桶的批发价．求甲种消毒液购买多少桶时，所需资金总额最少？最少总金额是多少元？
五．解一元一次不等式（共1小题）
5．（2020•通辽）用※定义一种新运算：对于任意实数m和n，规定m※n＝m2n﹣mn﹣3n，如：1※2＝12×2﹣1×2﹣3×2＝﹣6．
（1）求（﹣2）※；
（2）若3※m≥﹣6，求m的取值范围，并在所给的数轴上表示出解集．

六．一元一次不等式的应用（共1小题）
6．（2020•通辽）某服装专卖店计划购进A，B两种型号的精品服装．已知2件A型服装和3件B型服装共需4600元；1件A型服装和2件B型服装共需2800元．
（1）求A，B型服装的单价；
（2）专卖店要购进A，B两种型号服装60件，其中A型件数不少于B型件数的2倍，如果B型打七五折，那么该专卖店至少需要准备多少货款？
七．解一元一次不等式组（共1小题）
7．（2022•通辽）先化简，再求值：（a﹣）÷，请从不等式组的整数解中选择一个合适的数求值．
八．一次函数的应用（共1小题）
8．（2022•通辽）为落实“双减”政策，丰富课后服务的内容，某学校计划到甲、乙两个体育专卖店购买一批新的体育用品，两个商店的优惠活动如下：
甲：所有商品按原价8.5折出售；
乙：一次购买商品总额不超过300元的按原价付费，超过300元的部分打7折．
设需要购买体育用品的原价总额为x元，去甲商店购买实付y甲元，去乙商店购买实付y乙元，其函数图象如图所示．
（1）分别求y甲，y乙关于x的函数关系式；
（2）两图象交于点A，求点A坐标；
（3）请根据函数图象，直接写出选择去哪个体育专卖店购买体育用品更合算．

九．二次函数综合题（共3小题）
9．（2022•通辽）如图，抛物线y＝﹣x2+bx+c与x轴交于A，B两点，与y轴交于C点，直线BC方程为y＝x﹣3．
（1）求抛物线的解析式；
（2）点P为抛物线上一点，若S△PBC＝S△ABC，请直接写出点P的坐标；
（3）点Q是抛物线上一点，若∠ACQ＝45°，求点Q的坐标．

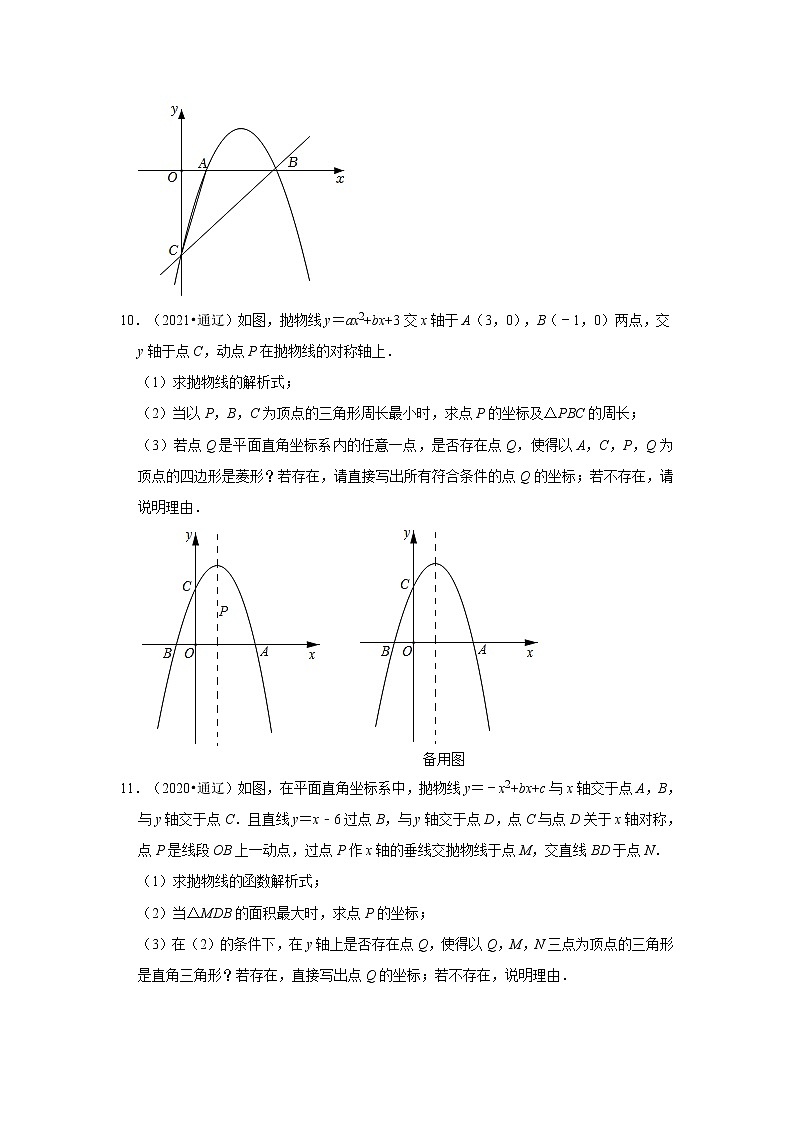
10．（2021•通辽）如图，抛物线y＝ax2+bx+3交x轴于A（3，0），B（﹣1，0）两点，交y轴于点C，动点P在抛物线的对称轴上．
（1）求抛物线的解析式；
（2）当以P，B，C为顶点的三角形周长最小时，求点P的坐标及△PBC的周长；
（3）若点Q是平面直角坐标系内的任意一点，是否存在点Q，使得以A，C，P，Q为顶点的四边形是菱形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．

11．（2020•通辽）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于点A，B，与y轴交于点C．且直线y＝x﹣6过点B，与y轴交于点D，点C与点D关于x轴对称，点P是线段OB上一动点，过点P作x轴的垂线交抛物线于点M，交直线BD于点N．
（1）求抛物线的函数解析式；
（2）当△MDB的面积最大时，求点P的坐标；
（3）在（2）的条件下，在y轴上是否存在点Q，使得以Q，M，N三点为顶点的三角形是直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由．

一十．四边形综合题（共1小题）
12．（2022•通辽）已知点E在正方形ABCD的对角线AC上，正方形AFEG与正方形ABCD有公共点A．
（1）如图1，当点G在AD上，F在AB上，求的值为多少；
（2）将正方形AFEG绕A点逆时针方向旋转α（0°＜α＜90°），如图2，求的值为多少；
（3）AB＝8，AG＝AD，将正方形AFEG绕A逆时针方向旋转α（0°＜α＜360°），当C，G，E三点共线时，请直接写出DG的长度．


一十一．切线的判定与性质（共1小题）
13．（2021•通辽）如图，AB是⊙O的直径，过点A作⊙O的切线AC，点P是射线AC上的动点，连接OP，过点B作BD∥OP，交⊙O于点D，连接PD．
（1）求证：PD是⊙O的切线；
（2）当四边形POBD是平行四边形时，求∠APO的度数．

一十二．正多边形和圆（共1小题）
14．（2020•通辽）中心为O的正六边形ABCDEF的半径为6cm，点P，Q同时分别从A，D两点出发，以1cm/s的速度沿AF，DC向终点F，C运动，连接PB，PE，QB，QE，设运动时间为t（s）．
（1）求证：四边形PBQE为平行四边形；
（2）求矩形PBQE的面积与正六边形ABCDEF的面积之比．

一十三．几何变换综合题（共1小题）
15．（2021•通辽）已知△AOB和△MON都是等腰直角三角形（OA＜OM＜OA），∠AOB＝∠MON＝90°．
（1）如图1，连接AM，BN，求证：AM＝BN；
（2）将△MON绕点O顺时针旋转．
①如图2，当点M恰好在AB边上时，求证：AM2+BM2＝2OM2；
②当点A，M，N在同一条直线上时，若OA＝4，OM＝3，请直接写出线段AM的长．

一十四．相似三角形的判定与性质（共1小题）
16．（2020•通辽）如图，⊙O的直径AB交弦（不是直径）CD于点P，且PC2＝PB•PA，求证：AB⊥CD．

一十五．特殊角的三角函数值（共1小题）
17．（2022•通辽）计算：•+4|1﹣|sin60°﹣（）﹣1．
一十六．解直角三角形（共1小题）
18．（2022•通辽）如图，在Rt△AOB中，∠AOB＝90°，以O为圆心，OB的长为半径的圆交边AB于点D，点C在边OA上且CD＝AC，延长CD交OB的延长线于点E．
（1）求证：CD是圆的切线；
（2）已知sin∠OCD＝，AB＝4，求AC长度及阴影部分面积．

一十七．解直角三角形的应用（共1小题）
19．（2022•通辽）某型号飞机的机翼形状如图所示，根据图中数据计算AB的长度（结果保留小数点后一位，≈1.7）．

一十八．解直角三角形的应用-仰角俯角问题（共1小题）
20．（2020•通辽）从A处看一栋楼顶部的仰角为α，看这栋楼底部的俯角为β，A处与楼的水平距离AD为90m．若tanα＝0.27，tanβ＝2.73，求这栋楼高．

一十九．解直角三角形的应用-方向角问题（共1小题）
21．（2021•通辽）如图，一段河流自西向东，河岸笔直，且两岸平行．为测量其宽度，小明在南岸边B处测得对岸边A处一棵大树位于北偏东60°方向，他以1.5m/s的速度沿着河岸向东步行40s后到达C处，此时测得大树位于北偏东45°方向，试计算此段河面的宽度（结果取整数，参考数据：≈1.732）

二十．频数（率）分布直方图（共1小题）
22．（2021•通辽）暑期将至，某校组织学生进行“防溺水”安全知识竞赛，老师从中随机抽取了部分学生的成绩（得分取整数，满分为100分），整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图．

其中A组的频数a比B组的频数b小15．请根据以上信息，解答下列问题：
（1）本次共抽取 　 　名学生，a的值为 　 　；
（2）在扇形统计图中，n＝　 　，E组所占比例为 　 　%；
（3）补全频数分布直方图；
（4）若全校共有1500名学生，请根据抽样调查的结果，估计成绩在80分以上的学生人数．
二十一．条形统计图（共2小题）
23．（2022•通辽）某学校在本校开展了四项“课后服务”项目（项目A：足球；项目B：篮球；项目C：跳绳；项目D：书法），要求每名学生必选且只能选修其中一项，为了解学生的选修情况，学校决定进行抽样调查，并根据收集的数据绘制了图1和图2两幅不完整的统计图．
（1）本次调查的学生共有 　 　人；在扇形统计图中，B所对应的扇形的圆心角的度数是 　 　°；
（2）将条形统计图补充完整；
（3）若全校共有1200名学生，估计该校选修篮球和跳绳两个项目的总人数．

24．（2020•通辽）某校研究学生的课余爱好情况，采取抽样调查的方法，从阅读、运动、娱乐、上网四个方面调查了若干名学生的兴趣爱好，并将调查结果绘制成如图所示的两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）在这次调查中，共调查了多少名学生；
（2）补全条形统计图；
（3）若该校爱好运动的学生共有800名，则该校学生总数大约有多少名．
二十二．列表法与树状图法（共3小题）
25．（2022•通辽）如图，一个圆环被4条线段分成4个区域，现有2022年冬奥会吉祥物“冰墩墩”和“雪容融”各一个，将这两个吉祥物放在任意两个区域内：
（1）求：吉祥物“冰墩墩”放在区域①的概率 　 　；
（2）求：吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的概率．（用树状图或列表法表示）

26．（2021•通辽）如图，甲、乙两个转盘均被分成3个面积相等的扇形，每个扇形中都标有相应的数字，同时转动两个转盘（当指针指在边界线上时视为无效，需重新转动转盘），当转盘停止后，把甲、乙两个转盘中指针所指数字分别记为x，y．请用树状图或列表法求点（x，y）落在平面直角坐标系第一象限内的概率．

27．（2020•通辽）甲口袋中装有2个相同小球，它们分别写有数字1，2；乙口袋中装有3个相同小球，它们分别写有数字3，4，5；丙口袋中装有2个相同小球，它们分别写有数字6，7．从三个口袋各随机取出1个小球．用画树状图或列表法求：
（1）取出的3个小球上恰好有一个偶数的概率；
（2）取出的3个小球上全是奇数的概率．

参考答案与试题解析
一．实数的运算（共1小题）
1．（2021•通辽）计算：（）﹣1+（π﹣3）0﹣2cos30°+|3﹣|．
【解答】解：原式＝2+1﹣2×+2
＝﹣
＝．
二．分式的化简求值（共1小题）
2．（2021•通辽）先化简，再求值：（+x﹣1）÷，其中x满足x2﹣x﹣2＝0．
【解答】解：原式＝•
＝•
＝x（x+1）
＝x2+x，
解方程x2﹣x﹣2＝0，得x1＝2，x2＝﹣1，
∵x+1≠0，
∴x≠﹣1，
当x＝2时，原式＝22+2＝6．
三．解分式方程（共1小题）
3．（2020•通辽）解方程：＝．
【解答】解：方程两边都乘以x（x﹣2）得，
2x＝3x﹣6，
解得x＝6，
检验：当x＝6时，x（x﹣2）＝6×4＝24≠0，
所以x＝6是分式方程的解．
因此，原分式方程的解是x＝6．
四．分式方程的应用（共1小题）
4．（2021•通辽）为做好新冠疫情的防控工作，某单位需购买甲、乙两种消毒液，经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元，该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液．
（1）求甲、乙两种消毒液的零售价分别是每桶多少元？
（2）由于疫情防控进入常态化，该单位需再次购买两种消毒液共300桶，且甲种消毒液的桶数不少于乙种消毒液桶数的．由于购买量大，甲、乙两种消毒液分别获得了20元/桶、15元/桶的批发价．求甲种消毒液购买多少桶时，所需资金总额最少？最少总金额是多少元？
【解答】解：（1）设乙种消毒液的零售价为x元/桶，则甲种消毒液的零售价为（x+6）元/桶，
依题意得：＝，
解得：x＝24，
经检验，x＝24是原方程的解，且符合题意，
∴x+6＝30．
答：甲种消毒液的零售价为30元/桶，乙种消毒液的零售价为24元/桶．
（2）设购买甲种消毒液m桶，则购买乙种消毒液（300﹣m）桶，
依题意得：m≥（300﹣m），
解得：m≥75．
设所需资金总额为w元，则w＝20m+15（300﹣m）＝5m+4500，
∵5＞0，
∴w随m的增大而增大，
∴当m＝75时，w取得最小值，最小值＝5×75+4500＝4875．
答：当甲种消毒液购买75桶时，所需资金总额最少，最少总金额是4875元．
五．解一元一次不等式（共1小题）
5．（2020•通辽）用※定义一种新运算：对于任意实数m和n，规定m※n＝m2n﹣mn﹣3n，如：1※2＝12×2﹣1×2﹣3×2＝﹣6．
（1）求（﹣2）※；
（2）若3※m≥﹣6，求m的取值范围，并在所给的数轴上表示出解集．

【解答】解：（1）（﹣2）※＝（﹣2）2×﹣（﹣2）×﹣3＝4+2﹣3＝3；
（2）3※m≥﹣6，
则32m﹣3m﹣3m≥﹣6，
解得：m≥﹣2，
将解集表示在数轴上如下：

六．一元一次不等式的应用（共1小题）
6．（2020•通辽）某服装专卖店计划购进A，B两种型号的精品服装．已知2件A型服装和3件B型服装共需4600元；1件A型服装和2件B型服装共需2800元．
（1）求A，B型服装的单价；
（2）专卖店要购进A，B两种型号服装60件，其中A型件数不少于B型件数的2倍，如果B型打七五折，那么该专卖店至少需要准备多少货款？
【解答】解：（1）设A型服装的单价为x元，B型服装的单价为y元，
依题意，得：，
解得：．
答：A型服装的单价为800元，B型服装的单价为1000元．
（2）设购进B型服装m件，则购进A型服装（60﹣m）件，
依题意，得：60﹣m≥2m，
解得：m≤20．
设该专卖店需要准备w元的货款，则w＝800（60﹣m）+1000×0.75m＝﹣50m+48000，
∵k＝﹣50，
∴w随m的增大而减小，
∴当m＝20时，w取得最小值，最小值＝﹣50×20+48000＝47000．
答：该专卖店至少需要准备47000元货款．
七．解一元一次不等式组（共1小题）
7．（2022•通辽）先化简，再求值：（a﹣）÷，请从不等式组的整数解中选择一个合适的数求值．
【解答】解：（a﹣）÷
＝•
＝•
＝a（a+2）
＝a2+2a，
，
解得：﹣1＜a≤2，
∴该不等式组的整数解为：0，1，2，
∵a≠0，a﹣2≠0，
∴a≠0且a≠2，
∴a＝1，
∴当a＝1时，原式＝12+2×1
＝1+2
＝3．
八．一次函数的应用（共1小题）
8．（2022•通辽）为落实“双减”政策，丰富课后服务的内容，某学校计划到甲、乙两个体育专卖店购买一批新的体育用品，两个商店的优惠活动如下：
甲：所有商品按原价8.5折出售；
乙：一次购买商品总额不超过300元的按原价付费，超过300元的部分打7折．
设需要购买体育用品的原价总额为x元，去甲商店购买实付y甲元，去乙商店购买实付y乙元，其函数图象如图所示．
（1）分别求y甲，y乙关于x的函数关系式；
（2）两图象交于点A，求点A坐标；
（3）请根据函数图象，直接写出选择去哪个体育专卖店购买体育用品更合算．

【解答】解：（1）由题意可得，
y甲＝0.85x，
当0≤x≤300时，y乙＝x，
当x＞300时，y乙＝300+（x﹣300）×0.7＝0.7x+90，
则y乙＝；
（2）令0.85x＝0.7x+90，
解得x＝600，
将x＝600代入0.85x得，0.85×600＝510，
即点A的坐标为（600，510）；
（3）由图象可得，
当x＜600时，去甲体育专卖店购买体育用品更合算；当x＝600时，两家体育专卖店购买体育用品一样合算；当x＞600时，去乙体育专卖店购买体育用品更合算．
九．二次函数综合题（共3小题）
9．（2022•通辽）如图，抛物线y＝﹣x2+bx+c与x轴交于A，B两点，与y轴交于C点，直线BC方程为y＝x﹣3．
（1）求抛物线的解析式；
（2）点P为抛物线上一点，若S△PBC＝S△ABC，请直接写出点P的坐标；
（3）点Q是抛物线上一点，若∠ACQ＝45°，求点Q的坐标．

【解答】解：（1）在y＝x﹣3中，令x＝0，则y＝﹣3，
∴C（0，﹣3），
令y＝0，则x＝3，
∴B（3，0），
将B、C两点代入y＝﹣x2+bx+c，
∴，
解得，
∴y＝﹣x2+4x﹣3；
（2）令y＝0，则﹣x2+4x﹣3＝0，
解得x＝1或x＝3，
∴A（1，0），
∴AB＝2，
∴S△ABC＝×2×3＝3，
∵S△PBC＝S△ABC，
∴S△PBC＝，
过点P作PQ⊥x轴交BC于点Q，
设P（t，﹣t2+4t﹣3），则Q（t，t﹣3），
∴PQ＝|﹣t2+3t|，
∴＝×3×|﹣t2+3t|，
解得t＝或t＝，
∴P点坐标为（，）或（，）或（，）或（，）；
（3）过点B作BE⊥BC交CQ于点E，过E点作EF⊥x轴交于F，
∵OB＝OC，
∴∠OCB＝45°，
∵∠ACQ＝45°，
∴∠BCQ＝∠OCA，
∵OA＝1，
∴tan∠OCA＝，
∴tan∠BCE＝＝，
∵BC＝3，
∴BE＝，
∵∠OBC＝45°，
∴∠EBF＝45°，
∴EF＝BF＝1，
∴E（4，﹣1），
设直线CE的解析式为y＝kx+b，
∴，
解得，
∴y＝x﹣3，
联立方程组，
解得（舍）或，
∴Q（，﹣）．


10．（2021•通辽）如图，抛物线y＝ax2+bx+3交x轴于A（3，0），B（﹣1，0）两点，交y轴于点C，动点P在抛物线的对称轴上．
（1）求抛物线的解析式；
（2）当以P，B，C为顶点的三角形周长最小时，求点P的坐标及△PBC的周长；
（3）若点Q是平面直角坐标系内的任意一点，是否存在点Q，使得以A，C，P，Q为顶点的四边形是菱形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．

【解答】解：（1）∵抛物线y＝ax2+bx+3交x轴于A（3，0），B（﹣1，0）两点，
∴，
解得：，
∴该抛物线的解析式为y＝﹣x2+2x+3；
（2）在y＝﹣x2+2x+3中，令x＝0，得y＝3，
∴C（0，3），
∵△PBC的周长为：PB+PC+BC，BC是定值，
∴当PB+PC最小时，△PBC的周长最小．
如图1，点A、B关于对称轴l对称，连接AC交l于点P，则点P为所求的点．
∵AP＝BP，
∴△PBC周长的最小值是AC+BC，
∵A（3，0），B（﹣1，0），C（0，3），
∴AC＝3，BC＝．
∴△PBC周长的最小值是：3+．
抛物线对称轴为直线x＝﹣＝1，
设直线AC的解析式为y＝kx+c，将A（3，0），C（0，3）代入，得：
，
解得：，
∴直线AC的解析式为y＝﹣x+3，
∴P（1，2）；
（3）存在．
设P（1，t），Q（m，n）
∵A（3，0），C（0，3），
则AC2＝32+32＝18，
AP2＝（1﹣3）2+t2＝t2+4，
PC2＝12+（t﹣3）2＝t2﹣6t+10，
∵四边形ACPQ是菱形，
∴分三种情况：以AP为对角线或以AC为对角线或以CP为对角线，
①当以AP为对角线时，则CP＝CA，如图2，
∴t2﹣6t+10＝18，
解得：t＝3±，
∴P1（1，3﹣），P2（1，3+），
∵四边形ACPQ是菱形，
∴AP与CQ互相垂直平分，即AP与CQ的中点重合，
当P1（1，3﹣）时，
∴＝，＝，
解得：m＝4，n＝﹣，
∴Q1（4，﹣），
当P2（1，3+）时，
∴＝，＝，
解得：m＝4，n＝，
∴Q2（4，），
②以AC为对角线时，则PC＝AP，如图3，
∴t2﹣6t+10＝t2+4，
解得：t＝1，
∴P3（1，1），
∵四边形APCQ是菱形，
∴AC与PQ互相垂直平分，即AC与CQ中点重合，
∴＝，＝，
解得：m＝2，n＝2，
∴Q3（2，2），
③当以CP为对角线时，则AP＝AC，如图4，
∴t2+4＝18，
解得：t＝±，
∴P4（1，），P5（1，﹣），
∵四边形ACQP是菱形，
∴AQ与CP互相垂直平分，即AQ与CP的中点重合，
∴＝，＝，
解得：m＝﹣2，n＝3，
∴Q4（﹣2，3+），Q5（﹣2，3﹣），
综上所述，符合条件的点Q的坐标为：Q1（4，﹣），Q2（4，），Q3（2，2），Q4（﹣2，3+），Q5（﹣2，3﹣）．




11．（2020•通辽）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于点A，B，与y轴交于点C．且直线y＝x﹣6过点B，与y轴交于点D，点C与点D关于x轴对称，点P是线段OB上一动点，过点P作x轴的垂线交抛物线于点M，交直线BD于点N．
（1）求抛物线的函数解析式；
（2）当△MDB的面积最大时，求点P的坐标；
（3）在（2）的条件下，在y轴上是否存在点Q，使得以Q，M，N三点为顶点的三角形是直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由．

【解答】解：（1）令y＝0，得y＝x﹣6＝0，
解得x＝6，
∴B（6，0），
令x＝0，得y＝x﹣6＝﹣6，
∴D（0，﹣6），
∵点C与点D关于x轴对称，
∴C（0，6），
把B、C点坐标代入y＝﹣x2+bx+c中，得
，
解得，，
∴抛物线的解析式为：y＝﹣x2+5x+6；
（2）设P（m，0），则M（m，﹣m2+5m+6），N（m，m﹣6），
则MN＝﹣m2+4m+12，
∴S△MDB＝＝﹣3m2+12m+36＝﹣3（m﹣2）2+48，
∵﹣3＜0，
∴当m＝2时，△MDB的面积最大，
此时，P点的坐标为（2，0）；

（3）由（2）知，M（2，12），N（2，﹣4），
当∠QMN＝90°时，QM∥x轴，则Q（0，12）；
当∠MNQ＝90°时，NQ∥x轴，则Q（0，﹣4）；
当∠MQN＝90°时，设Q（0，n），则QM2+QN2＝MN2，
即4+（12﹣n）2+4+（n+4）2＝（12+4）2，
解得，n＝4±2，
∴Q（0，4+2）或（0，4﹣2）．
综上，存在以Q，M，N三点为顶点的三角形是直角三角形．其Q点坐标为（0，12）或（0，﹣4）或（0，4+2）或（0，4﹣2）．
一十．四边形综合题（共1小题）
12．（2022•通辽）已知点E在正方形ABCD的对角线AC上，正方形AFEG与正方形ABCD有公共点A．
（1）如图1，当点G在AD上，F在AB上，求的值为多少；
（2）将正方形AFEG绕A点逆时针方向旋转α（0°＜α＜90°），如图2，求的值为多少；
（3）AB＝8，AG＝AD，将正方形AFEG绕A逆时针方向旋转α（0°＜α＜360°），当C，G，E三点共线时，请直接写出DG的长度．


【解答】解：（1）∵四边形ABCD是正方形，四边形CEGF是正方形，
∴∠AGE＝∠D＝90°，∠DAC＝45°，
∴，GE∥CD，
∴，
∴CE＝DG，
∴＝＝2；

（2）连接AE，

由旋转性质知∠CAE＝∠DAG＝α，
在Rt△AEG和Rt△ACD中，
＝cos45°＝、＝cos45°＝，
∴，
∴△ADG∽△ACE，
∴＝，
∴＝；

（3）①如图：

由（2）知△ADG∽△ACE，
∴，
∴DG＝CE，
∵四边形ABCD是正方形，
∴AD＝BC＝8，AC＝＝16，
∵AG＝AD，
∴AG＝AD＝8，
∵四边形CEGF是矩形，
∴∠AGE＝90°，GE＝AG＝8，
∵C，G，E三点共线．
∴CG＝＝＝8，
∴CE＝CG﹣EG＝8﹣8，
∴DG＝CE＝4﹣4；
②如图：

由（2）知△ADG∽△ACE，
∴，
∴DG＝CE，
∵四边形ABCD是正方形，
∴AD＝BC＝8，AC＝＝16，
∵AG＝AD，
∴AG＝AD＝8，
∵四边形CEGF是矩形，
∴∠AGE＝90°，GE＝AG＝8，
∵C，G，E三点共线．
∴∠AGC＝90°
∴CG＝＝＝8，
∴CE＝CG+EG＝8+8，
∴DG＝CE＝4+4．
综上，当C，G，E三点共线时，DG的长度为4﹣4或4+4．
一十一．切线的判定与性质（共1小题）
13．（2021•通辽）如图，AB是⊙O的直径，过点A作⊙O的切线AC，点P是射线AC上的动点，连接OP，过点B作BD∥OP，交⊙O于点D，连接PD．
（1）求证：PD是⊙O的切线；
（2）当四边形POBD是平行四边形时，求∠APO的度数．

【解答】（1）证明：连接OD，

∵PA切⊙O于A，
∴PA⊥AB，
即∠PAO＝90°，
∵OP∥BD，
∴∠DBO＝∠AOP，∠BDO＝∠DOP，
∵OD＝OB，
∴∠BDO＝∠DBO，
∴∠DOP＝∠AOP，
在△AOP和△DOP中
，
∴△AOP≌△DOP（SAS），
∴∠PDO＝∠PAO，
∵∠PAO＝90°，
∴∠PDO＝90°，
即OD⊥PD，
∵OD过O，
∴PD是⊙O的切线；

（2）解：
由（1）知：△AOP≌△DOP，
∴PA＝PD，
∵四边形POBD是平行四边形，
∴PD＝OB，
∵OB＝OA，
∴PA＝OA，
∴∠APO＝∠AOP，
∵∠PAO＝90°，
∴∠APO＝∠AOP＝45°．
一十二．正多边形和圆（共1小题）
14．（2020•通辽）中心为O的正六边形ABCDEF的半径为6cm，点P，Q同时分别从A，D两点出发，以1cm/s的速度沿AF，DC向终点F，C运动，连接PB，PE，QB，QE，设运动时间为t（s）．
（1）求证：四边形PBQE为平行四边形；
（2）求矩形PBQE的面积与正六边形ABCDEF的面积之比．

【解答】（1）证明：∵六边形ABCDEF是正六边形，
∴AB＝BC＝CD＝DE＝EF＝FA，∠A＝∠ABC＝∠C＝∠D＝∠DEF＝∠F，
∵点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，
∴AP＝DQ＝t，PF＝QC＝6﹣t，
在△ABP和△DEQ中，
，
∴△ABP≌△DEQ（SAS），
∴BP＝EQ，
同理可证PE＝QB，
∴四边形PEQB为平行四边形．
（2）解：连接BE、OA，则∠AOB＝＝60°，
∵OA＝OB，
∴△AOB是等边三角形，
∴AB＝OA＝6，BE＝2OB＝12，
当t＝0时，点P与A重合，Q与D重合，四边形PBQE即为四边形ABDE，如图1所示：
则∠EAF＝∠AEF＝30°，
∴∠BAE＝∠BAF﹣∠FAE＝120°﹣30°＝90°，
∴此时四边形ABDE是矩形，即四边形PBQE是矩形．
当t＝6时，点P与F重合，Q与C重合，四边形PBQE即为四边形FBCE，如图2所示：
同法可知∠BFE＝90°，此时四边形PBQE是矩形．
综上所述，t＝0s或6s时，四边形PBQE是矩形，
∴AE＝＝6，
∴矩形PBQE的面积＝矩形ABDE的面积＝AB×AE＝6×6＝36；
∵正六边形ABCDEF的面积＝6△AOB的面积＝6×矩形ABDE的面积＝6××36＝54，
∴矩形PBQE的面积与正六边形ABCDEF的面积之比＝．


一十三．几何变换综合题（共1小题）
15．（2021•通辽）已知△AOB和△MON都是等腰直角三角形（OA＜OM＜OA），∠AOB＝∠MON＝90°．
（1）如图1，连接AM，BN，求证：AM＝BN；
（2）将△MON绕点O顺时针旋转．
①如图2，当点M恰好在AB边上时，求证：AM2+BM2＝2OM2；
②当点A，M，N在同一条直线上时，若OA＝4，OM＝3，请直接写出线段AM的长．

【解答】（1）证明：∵∠AOB＝∠MON＝90°，
∴∠AOB+∠AON＝∠MON+∠AON，
即∠AOM＝∠BON，
∵△AOB和△MON都是等腰直角三角形，
∴OA＝OB，OM＝ON，
∴△AOM≌△BON（SAS），
∴AM＝BN；

（2）①证明：连接BN，
∵∠AOB＝∠MON＝90°，
∴∠AOB﹣∠BOM＝∠MON﹣∠BOM，
即∠AOM＝∠BON，
∵△AOB和△MON都是等腰直角三角形，
∴OA＝OB，OM＝ON，
∴△AOM≌△BON（SAS），
∴∠MAO＝∠NBO＝45°，AM＝BN，
∴∠MBN＝90°，
∴MB2+BN2＝MN2，
∵△MON是等腰直角三角形，
∴MN2＝2ON2，
∴AM2+BM2＝2OM2；

②解：如图3，当点N在线段AM上时，连接BN，设BN＝x，
由（1）可知△AOM≌△BON，可得AM＝BN且AM⊥BN，
在Rt△ABN中，AN2+BN2＝AB2，
∵△AOB和△MON都是等腰直角三角形，OA＝4，OM＝3，
∴MN＝3，AB＝4，
∴（x﹣3）2+x2＝（4）2，
解得：x＝，
∴AM＝BN＝，
如图4，当点M在线段AN上时，连接BN，设BN＝x，
由（1）可知△AOM≌△BON，可得AM＝BN且AM⊥BN，
在Rt△ABN中，AN2+BN2＝AB2，
∵△AOB和△MON都是等腰直角三角形，OA＝4，OM＝3，
∴MN＝3，AB＝4，
∴（x+3）2+x2＝（4）2，
解得：x＝，
∴AM＝BN＝，
综上所述，线段AM的长为或．
一十四．相似三角形的判定与性质（共1小题）
16．（2020•通辽）如图，⊙O的直径AB交弦（不是直径）CD于点P，且PC2＝PB•PA，求证：AB⊥CD．

【解答】证明：连接AC、BD，如图，
∵∠A＝∠D，∠C＝∠B，
∴△APC∽△DPB，
∴PC：PB＝PA：PD，
∴PC•PD＝PA•PB，
∵PC2＝PB•PA，
∴PC＝PD，
∵AB为直径，
∴AB⊥CD．

一十五．特殊角的三角函数值（共1小题）
17．（2022•通辽）计算：•+4|1﹣|sin60°﹣（）﹣1．
【解答】解：•+4|1﹣|sin60°﹣（）﹣1
＝2+4×（﹣1）×﹣2
＝2+2（﹣1）﹣2
＝2+6﹣2﹣2
＝4．
一十六．解直角三角形（共1小题）
18．（2022•通辽）如图，在Rt△AOB中，∠AOB＝90°，以O为圆心，OB的长为半径的圆交边AB于点D，点C在边OA上且CD＝AC，延长CD交OB的延长线于点E．
（1）求证：CD是圆的切线；
（2）已知sin∠OCD＝，AB＝4，求AC长度及阴影部分面积．

【解答】（1）证明：如图，连接OD，
∵AC＝CD，
∴∠A＝∠ADC＝∠BDE，
∵∠AOB＝90°，
∴∠A+∠ABO＝90°，
又∵OB＝OD，
∴∠OBD＝∠ODB，
∴∠ODB+∠BDE＝90°，
即OD⊥EC，
∵OD是半径，
∴EC是⊙O的切线；
（2）解：在Rt△COD中，由于sin∠OCD＝，
设OD＝4x，则OC＝5x，
∴CD＝＝3x＝AC，
在Rt△AOB中，OB＝OD＝4x，OA＝OC+AC＝8x，AB＝4，由勾股定理得，
OB2+OA2＝AB2，
即：（4x）2+（8x）2＝（4）2，
解得x＝1或x＝﹣1（舍去），
∴AC＝3x＝3，OC＝5x＝5，OB＝OD＝4x＝4，
∵∠ODC＝∠EOC＝90°，∠OCD＝∠ECO，
∴△COD∽△CEO，
∴＝，
即＝，
∴EC＝，
∴S阴影部分＝S△COE﹣S扇形
＝××4﹣
＝﹣4π
＝，
答：AC＝3，阴影部分的面积为．

一十七．解直角三角形的应用（共1小题）
19．（2022•通辽）某型号飞机的机翼形状如图所示，根据图中数据计算AB的长度（结果保留小数点后一位，≈1.7）．

【解答】解：如图，过点C、D分别作BE的平行线交BA的延长线于点M、N，
在Rt△BDE中，∠BDE＝90°﹣45°＝45°，
∴DE＝BE＝14m，
在Rt△ACM中，∠ACM＝60°，CM＝BE＝14m，
∴AM＝CM＝14（m），
∴AB＝BM﹣AM
＝CE﹣AM
＝20+14﹣14
≈10.2（m），
答：AB的长约为10.2m．

一十八．解直角三角形的应用-仰角俯角问题（共1小题）
20．（2020•通辽）从A处看一栋楼顶部的仰角为α，看这栋楼底部的俯角为β，A处与楼的水平距离AD为90m．若tanα＝0.27，tanβ＝2.73，求这栋楼高．

【解答】解：在Rt△ABD中，BD＝tanα•AD＝0.27×90＝24.3（米），
在Rt△ACD中，CD＝AD•tanβ＝90×2.73＝245.7（米），
∴BC＝BD+CD＝24.3+245.7＝270（米），
答：这栋楼高BC为270米．
一十九．解直角三角形的应用-方向角问题（共1小题）
21．（2021•通辽）如图，一段河流自西向东，河岸笔直，且两岸平行．为测量其宽度，小明在南岸边B处测得对岸边A处一棵大树位于北偏东60°方向，他以1.5m/s的速度沿着河岸向东步行40s后到达C处，此时测得大树位于北偏东45°方向，试计算此段河面的宽度（结果取整数，参考数据：≈1.732）

【解答】解：如图，作AD⊥BC于D．
由题意可知：BC＝1.5×40＝60（m），∠ABD＝90°﹣60°＝30°，∠ACD＝90°﹣45°＝45°，
在Rt△ACD中，∵tan∠ACD＝tan45°＝＝1，
∴AD＝CD，
在Rt△ABD中，∵tan∠ABD＝tan30°＝，
∴BD＝，
∵BC＝BD﹣CD＝﹣AD＝60（m），
∴AD＝30（+1）≈82（m），
答：此段河面的宽度约82m．

二十．频数（率）分布直方图（共1小题）
22．（2021•通辽）暑期将至，某校组织学生进行“防溺水”安全知识竞赛，老师从中随机抽取了部分学生的成绩（得分取整数，满分为100分），整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图．

其中A组的频数a比B组的频数b小15．请根据以上信息，解答下列问题：
（1）本次共抽取 　150　名学生，a的值为 　12　；
（2）在扇形统计图中，n＝　144　，E组所占比例为 　4　%；
（3）补全频数分布直方图；
（4）若全校共有1500名学生，请根据抽样调查的结果，估计成绩在80分以上的学生人数．
【解答】解：（1）A组的频数a比B组的频数b小15，A组的频率比B组的频率小18%﹣8%＝10%，
因此调查人数为：15÷10%＝150（人），
a＝150×8%＝12（人），
故答案为：150，12；
（2）360°×＝360°×40%＝144°，即n＝144，
“E组”所占的百分比为1﹣8%﹣18%﹣30%﹣40%＝4%，
故答案为：144，4；
（3）b＝a+15＝27（人），
“C组”频数为：150×30%＝45（人），
“E组”频数为：150×4%＝6（人），
补全频数分布直方图如图所示：

（4）1500×＝660（人），
答：估计成绩在80分以上的学生人数大约为660人．
二十一．条形统计图（共2小题）
23．（2022•通辽）某学校在本校开展了四项“课后服务”项目（项目A：足球；项目B：篮球；项目C：跳绳；项目D：书法），要求每名学生必选且只能选修其中一项，为了解学生的选修情况，学校决定进行抽样调查，并根据收集的数据绘制了图1和图2两幅不完整的统计图．
（1）本次调查的学生共有 　200　人；在扇形统计图中，B所对应的扇形的圆心角的度数是 　108　°；
（2）将条形统计图补充完整；
（3）若全校共有1200名学生，估计该校选修篮球和跳绳两个项目的总人数．

【解答】解：（1）本次调查的学生共有：30÷15%＝200（人），
在扇形统计图中，B所对应的扇形的圆心角的度数是：360°×＝108°；
故答案为：200，108；

（2）C项目的人数有：200﹣30﹣60﹣20＝90（人），
补全统计图如下：


（3）根据题意得：
1200×＝900（人），
答：估计该校选修篮球和跳绳两个项目的总人数有900人．
24．（2020•通辽）某校研究学生的课余爱好情况，采取抽样调查的方法，从阅读、运动、娱乐、上网四个方面调查了若干名学生的兴趣爱好，并将调查结果绘制成如图所示的两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）在这次调查中，共调查了多少名学生；
（2）补全条形统计图；
（3）若该校爱好运动的学生共有800名，则该校学生总数大约有多少名．
【解答】解：（1）40÷40%＝100（名），
即在这次调查中，共调查了100名学生；
（2）爱好上网的学生有：100×10%＝10（名），
爱好阅读的学生有：100﹣40﹣20﹣10＝30（名），
补全的条形统计图如右图所示；
（3）800÷40%＝2000（名），
答：该校学生总数大约有2000名．

二十二．列表法与树状图法（共3小题）
25．（2022•通辽）如图，一个圆环被4条线段分成4个区域，现有2022年冬奥会吉祥物“冰墩墩”和“雪容融”各一个，将这两个吉祥物放在任意两个区域内：
（1）求：吉祥物“冰墩墩”放在区域①的概率 　　；
（2）求：吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的概率．（用树状图或列表法表示）

【解答】解：（1）吉祥物“冰墩墩”放在区域①的概率是；
故答案为：；

（2）根据题意画图如下：

共有12种等可能的情况数，其中吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域有8种，
则吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的概率是＝．
26．（2021•通辽）如图，甲、乙两个转盘均被分成3个面积相等的扇形，每个扇形中都标有相应的数字，同时转动两个转盘（当指针指在边界线上时视为无效，需重新转动转盘），当转盘停止后，把甲、乙两个转盘中指针所指数字分别记为x，y．请用树状图或列表法求点（x，y）落在平面直角坐标系第一象限内的概率．

【解答】解：画树状图如图：

共有9种等可能的结果，点（x，y）落在平面直角坐标系第一象限内的结果有4种，
∴点（x，y）落在平面直角坐标系第一象限内的概率为．
27．（2020•通辽）甲口袋中装有2个相同小球，它们分别写有数字1，2；乙口袋中装有3个相同小球，它们分别写有数字3，4，5；丙口袋中装有2个相同小球，它们分别写有数字6，7．从三个口袋各随机取出1个小球．用画树状图或列表法求：
（1）取出的3个小球上恰好有一个偶数的概率；
（2）取出的3个小球上全是奇数的概率．
【解答】解：（1）画树状图为：

共有12种等可能的结果，其中取出的3个小球上恰好有一个偶数的结果数为5，
所以取出的3个小球上恰好有一个偶数的概率＝；
（2）取出的3个小球上全是奇数的结果数为2，
所以取出的3个小球上全是奇数的概率＝＝．