2021学年13.3.1 等腰三角形图文ppt课件

这是一份2021学年13.3.1 等腰三角形图文ppt课件，共18页。PPT课件主要包含了你能证明这个结论吗，你能得到什么结论呢，等腰三角形的判定等内容，欢迎下载使用。

1、理解等腰三角形的判定，体会等腰三角形“等边对等角”和“等角对等边”的区别.2、探索并掌握等腰三角形的判定的过程，并用以解决实际问题.
同学们，上节课我们学习了等腰三角形的哪些性质？
性质1：等腰三角形的两个底角相等.
性质2：等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.
思考：如果有一个三角形有两条边相等，那么它们所对的角相等.反之，如果一个三角形有两个角相等，那么它们所对的边有什么关系？
猜想：如果一个三角形有两个角相等，那么它们所对的边相等.
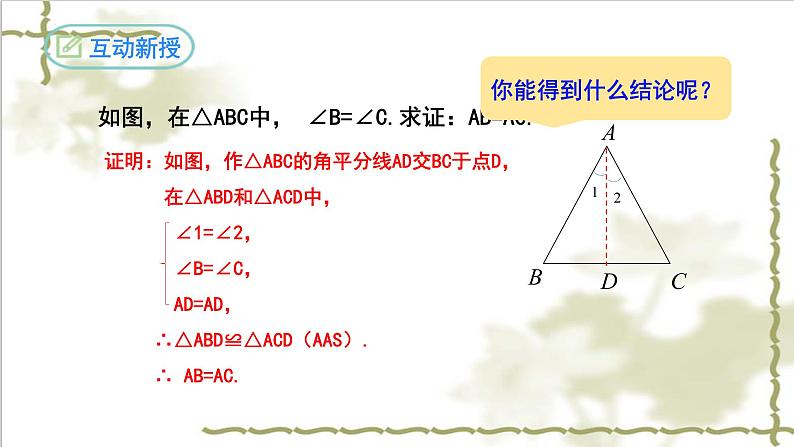
如图，在△ABC中， ∠B=∠C.求证：AB=AC.
证明：如图，作△ABC的角平分线AD交BC于点D， 在△ABD和△ACD中， ∠1=∠2， ∠B=∠C， AD=AD， ∴△ABD≌△ACD（AAS）. ∴ AB=AC.
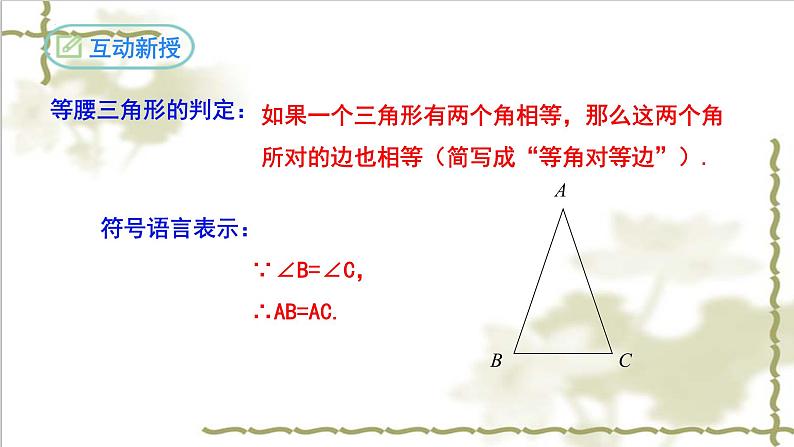
如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）.
符号语言表示： ∵∠B=∠C， ∴AB=AC.
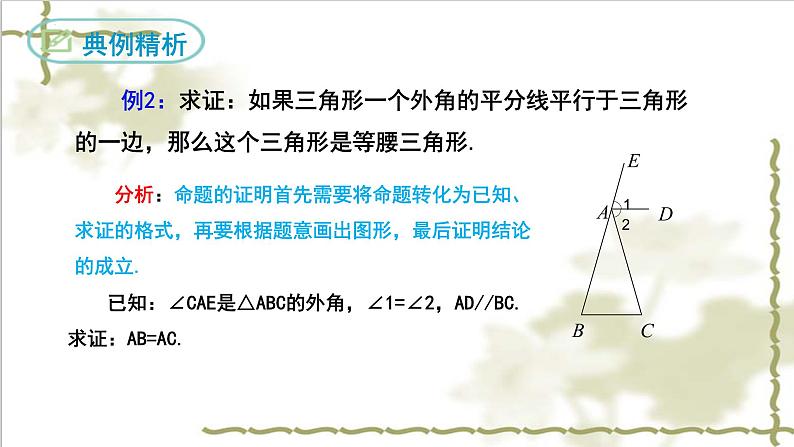
例2：求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形.
分析：命题的证明首先需要将命题转化为已知、求证的格式，再要根据题意画出图形，最后证明结论的成立.
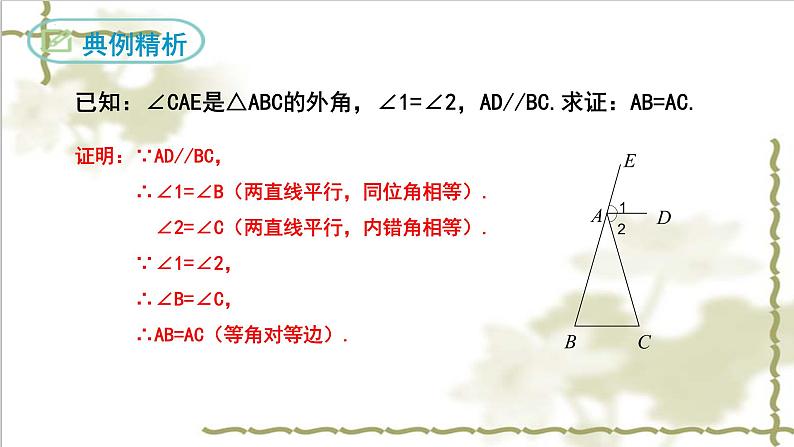
已知：∠CAE是△ABC的外角，∠1=∠2，AD//BC.求证：AB=AC.
已知：∠CAE是△ABC的外角，∠1=∠2，AD//BC.求证：AB=AC.
证明：∵AD//BC， ∴∠1=∠B（两直线平行，同位角相等）. ∠2=∠C（两直线平行，内错角相等）. ∵∠1=∠2， ∴∠B=∠C， ∴AB=AC（等角对等边）.
例2：已知等腰三角形底边长为a，底边上的高的长为h，求作这个等腰三角形.
（1）作线段AB=a.
（2）作线段AB的垂直平分线MN，与AB相交于点D.
（3）在MN上取一点C，使DC=h.
（4）连接AC，BC，则△ABC就是所求作的等腰三角形.
A.△ABC B.△ABD C.△ACD D.△ACE
1.如图，AD平分∠BAC，AD∥CE，则下列三角形一定是等腰三角形的是（ ）
2.如图，在△ABC中，O是三条角平分线的交点，过点O作DE∥BC交AB于点D，交AC于点E，若AB=6，AC=4，则△ADE的周长为____.
1.如图，∠A=36°，∠DBC=36°，∠C=72°，分别计算∠1，∠2的度数，并说明图中有哪些等腰三角形.
解：∵在△ABC中，∠A=36°，∠C=72°, ∴∠ABC=72°. ∵∠DBC=36°， ∴∠2=∠ABC-∠DBC=36°. ∵∠1=∠A+∠2=72°， ∴AD=BD=BC，AB=AC.图中的等腰三角形有△ABC，△ABD，△BCD.
2.如图，把一张长方形的纸沿着对角线折叠，重合部分是一个等腰三角形吗？为什么？
是等腰三角形．如图可证∠1=∠2．
3．如图，AC 和BD 相交于点O，且AB∥DC，OA =OB．求证：OC =OD．
证明：∵OA=OB， ∴∠A=∠B（等边对等角）． ∵AB∥DC， ∴∠A=∠C，∠B=∠D． ∴∠C=∠D． ∴OC=OD（等角对等边）．
如图，已知AB=AE，BC=DE，∠B=∠E，AF⊥CD，垂足为点F.求证：CF=FD.
证明：连接AC，AD. 在△ABC和△AED中， AB=AE， ∠B=∠E， BC=ED， ∴△ABC≌△AED（SAS）. ∴AC=AD. ∵AF⊥CD， ∴CF=FD.
1．等腰三角形的判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．2．等腰三角形的判定与性质的区别是条件和结论刚好相反．3．运用等腰三角形的判定与性质时，应注意在同一个三角形中．
如图，AD//BC，BD平分∠ABC.求证：AB=AD.
证明：∵BD平分∠ABC， ∴∠ABD=∠CBD. ∵AD//BC， ∴∠ADB=∠CBD. ∴∠ABD=∠ADB. ∴AB=AD.