人教版八年级上册12.2 三角形全等的判定教学课件ppt

这是一份人教版八年级上册12.2 三角形全等的判定教学课件ppt，共16页。PPT课件主要包含了符号语言表示，AC＝BD，AD＝BC，∠ABC＝∠BAD，AAS，∠BAC＝∠ABD等内容，欢迎下载使用。
1、理解并掌握直角三角形全等判定“斜边、直角边”条件的内容.2、熟练利用“斜边、直角边”条件证明两个直角三角形全等.3、通过探究判定三角形全等条件的过程，提高分析和解决问题的能力.
三条边分别相等的三角形全等（SSS）．
上节课我们学习了什么方法可以判定两个三角形全等？
除了上面的方法，还有其他方法能判定两个三角形全等吗？我们继续探索三角形全等的条件.
两边和它们的夹角分别相等的两个三角形全等（SAS）.
两角和它们的夹边分别相等的两个三角形全等（ASA）
两角分别相等且其中一组等角的对边相等的两个三角形全等（AAS）
思考：两个直角三角形中，已经有一对相等的直角，还需要满足几个条件就可以说明两个三角形全等？
（1）一边一锐角分别相等的两个直角三角形全等．（利用“ASA”或“AAS”）
（2）两直角边分别相等的两个直角三角形全等．（利用“SAS”）
如果满足斜边和一条直角边分别相等，这两个直角三角形全等吗？
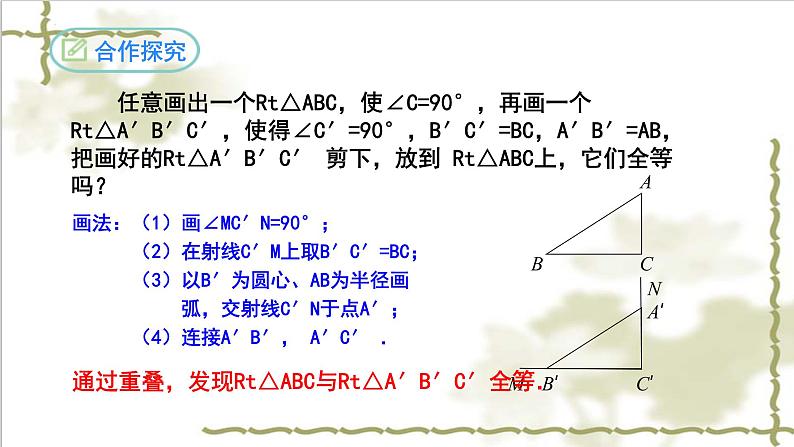
任意画出一个Rt△ABC，使∠C=90°，再画一个Rt△A′B′C′，使得∠C′=90°，B′C′=BC，A′B′=AB，把画好的Rt△A′B′C′ 剪下，放到 Rt△ABC上，它们全等吗？
画法：（1）画∠MC′N=90°； （2）在射线C′M上取B′C′=BC； （3）以B′为圆心、AB为半径画 弧，交射线C′N于点A′； （4）连接A′B′， A′C′ ．
通过重叠，发现Rt△ABC与Rt△A′B′C′全等．
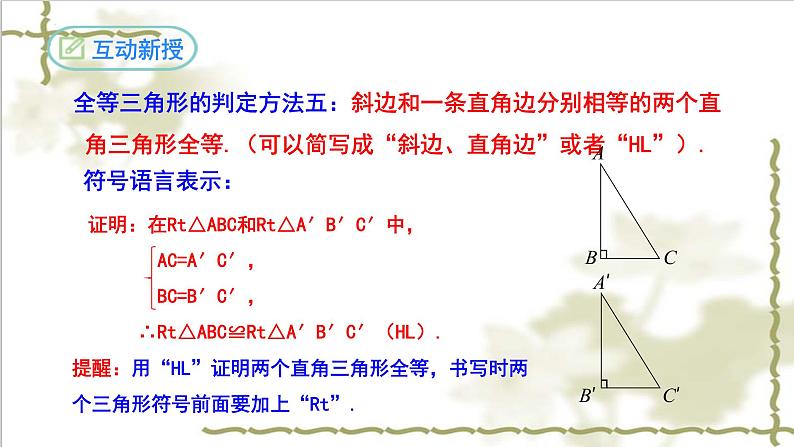
全等三角形的判定方法五：斜边和一条直角边分别相等的两个直角三角形全等.（可以简写成“斜边、直角边”或者“HL”）.
证明：在Rt△ABC和Rt△A′B′C′中， AC=A′C′， BC=B′C′， ∴Rt△ABC≌Rt△A′B′C′（HL）.
提醒：用“HL”证明两个直角三角形全等，书写时两个三角形符号前面要加上“Rt”.
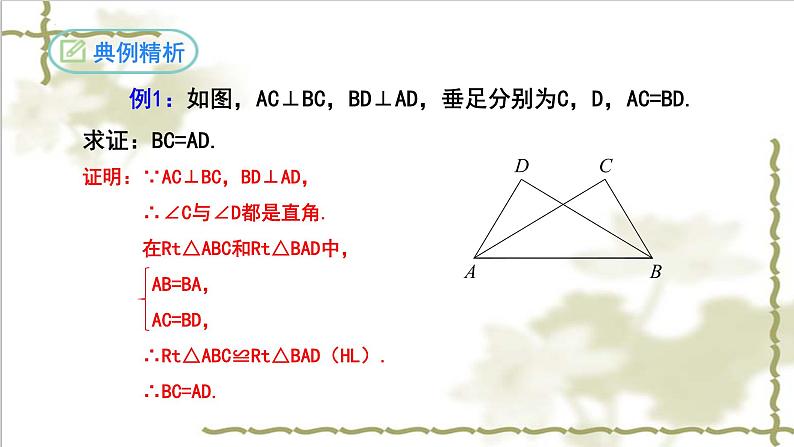
例1：如图，AC⊥BC，BD⊥AD，垂足分别为C，D，AC=BD.求证：BC=AD.
证明：∵AC⊥BC，BD⊥AD， ∴∠C与∠D都是直角. 在Rt△ABC和Rt△BAD中， AB=BA， AC=BD， ∴Rt△ABC≌Rt△BAD（HL）. ∴BC=AD.
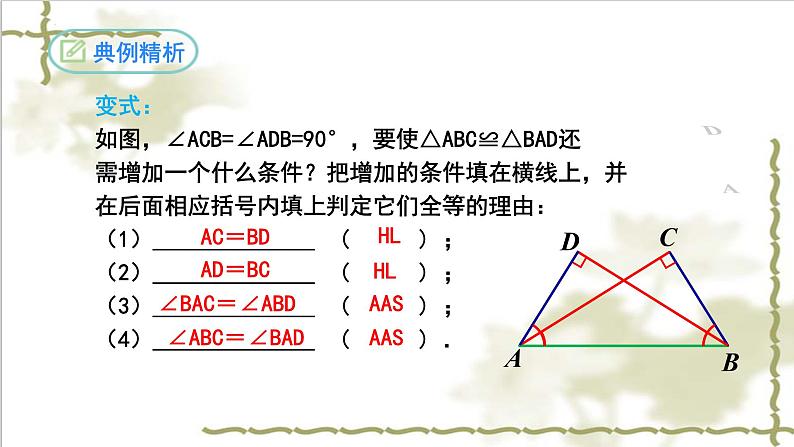
变式：如图，∠ACB=∠ADB=90°，要使△ABC≌△BAD还需增加一个什么条件？把增加的条件填在横线上，并在后面相应括号内填上判定它们全等的理由：（1）______________ ( ) ；（2）______________ ( ) ；（3）______________ ( ) ；（4）______________ ( ) ．
如图，AE⊥BC，DF⊥BC，E，F是垂足，且AE=DF，AB=DC，求证：∠ABC=∠DCB.
证明：∵AE⊥BC，DF⊥BC， ∴在Rt△ABE和Rt△DCF中， AE=DF AB=CD ∴Rt△ABE≌Rt△DCF(HL) ∴∠ABC=∠DCB．
1.如图，AB=CD，AE⊥BC，DF⊥BC，垂足分别为E，F，CE=BF.求证：AE=DF.
证明：∵CE=BF， ∴CE-FE=BF-EF，即CF=BE. 在Rt△ABE和Rt△DCF中， AB=DC， BE=CF， ∴Rt△ABE≌Rt△DCF（HL）. ∴AE=DF.
2.如图，C是路段AB的中点，两人从C同时出发，以相同的速度分别沿着两条直线行走，并同时到达D，E两地.DA⊥AB，EB⊥AB.D，E与路段AB的距离相等吗？为什么？
解：相等，理由如下： ∵C是路段AB的中点， ∴AC=BC. ∵同时出发，同时到达，且速度相同， ∴CD=CE. ∵DA⊥AB，EB⊥AB ∴△ACD和△BCE是直角三角形. 在Rt△ACD和Rt△BCE中， AC=BC， CD=CE， ∴ Rt△ACD≌Rt△BCE（HL）. ∴DA=DB.
1.已知：如图，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝DC.求证：BE＝DF.
证明：∵AC平分∠BAD， ∴∠DAC=∠BAC． ∵CE⊥AB于E，CF⊥AD于F， ∴∠AFC＝∠AEC. ∵AC=AC ， ∴△AFC≌△AEC（AAS）． ∴EC=FC．
在Rt△DCF和Rt△BCE中∴Rt△DCF≌Rt△BCE(HL)∴BE=DF．
1.三角形全等的判定：HL
2.利用HL解决实际问题
3.截止现在我们学习了几种三角形全等的判定方法？
（1）全等三角形的定义；（2）边边边（SSS）；（3）边角边（SAS）；（4）角边角（ASA）；（5）角角边（AAS）；（6）斜边、直角（HL）．
如图，AB=CD，AE⊥BC，DF⊥BC，垂足分别为E，F，CE=BF.求证：AE∥DF．
证明：∵CE=BF， ∴CE+EF=BF+EF，即BE=CF， 在Rt△AEB和Rt△DCF中， AB=CD BE=CF ∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF∥CD．